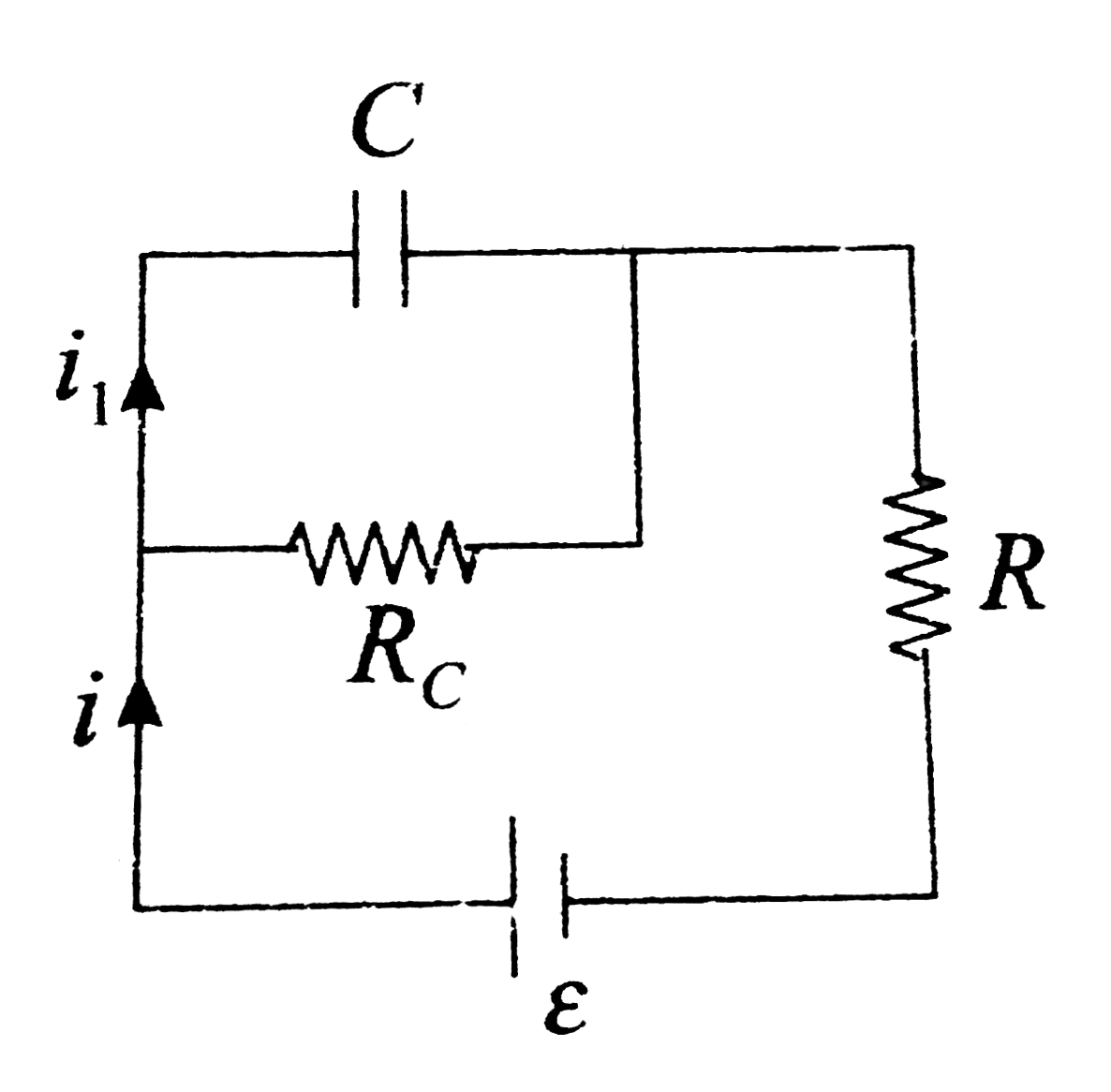
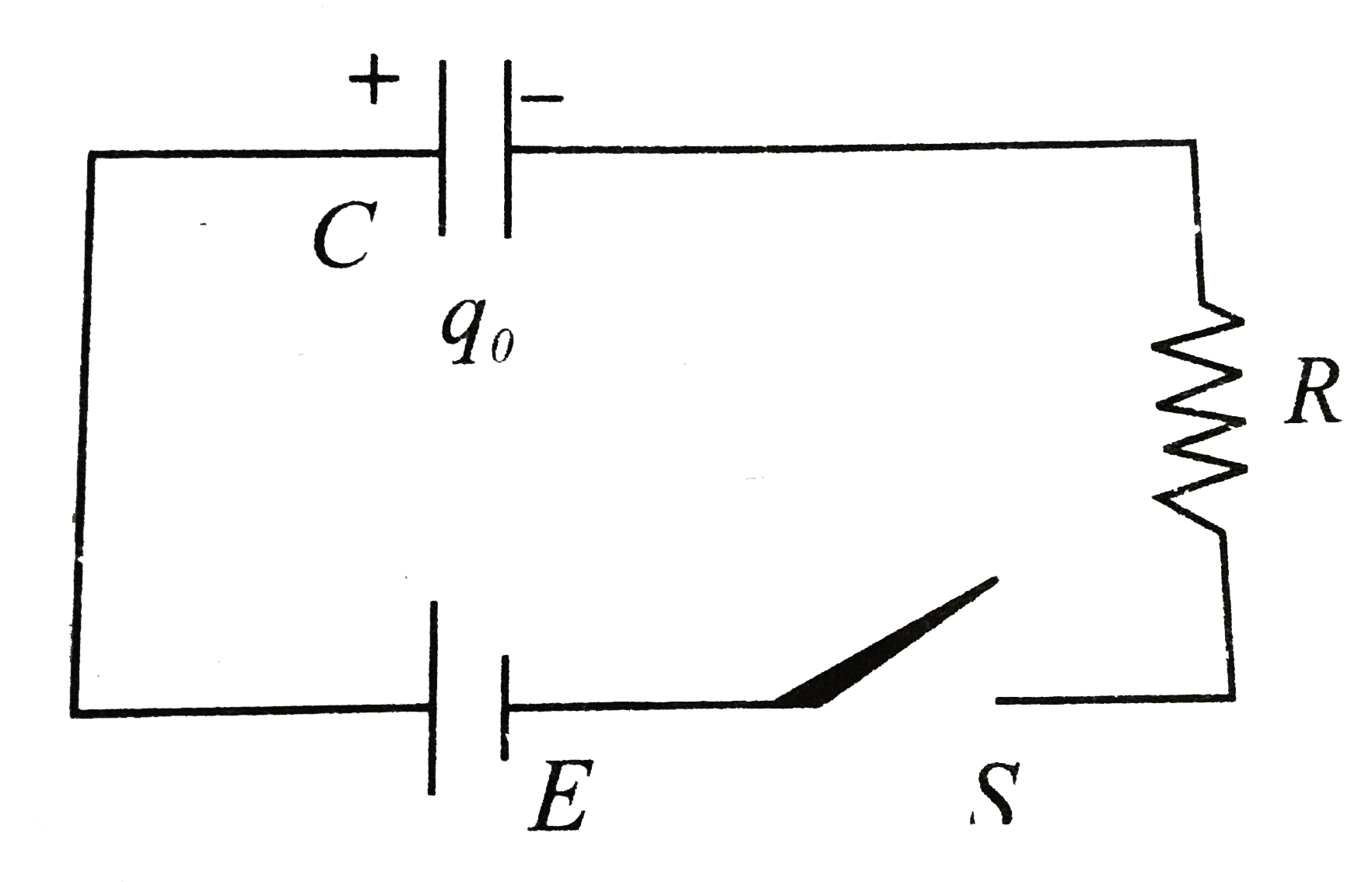
Consider a parallel pate capacitor of capactance C with partially conducting medium between its plates having a resistacne if this capacitor is connected to a battery of emf and a resistor R as shown in fig.
a. charge on the capacitor as a function of time.
The switch R as a function of time.

The equivalent circuit can be drawn as shown. Applying
Kirchhoff's law for the two loops,
(i)
(ii)
Eliminating I between (i) and (ii) we get
For capacitor
Solving, we get
Adding (i) and (ii), we get
Substituting for q, we get
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Single Correct72videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Multiple Correct16videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.250videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
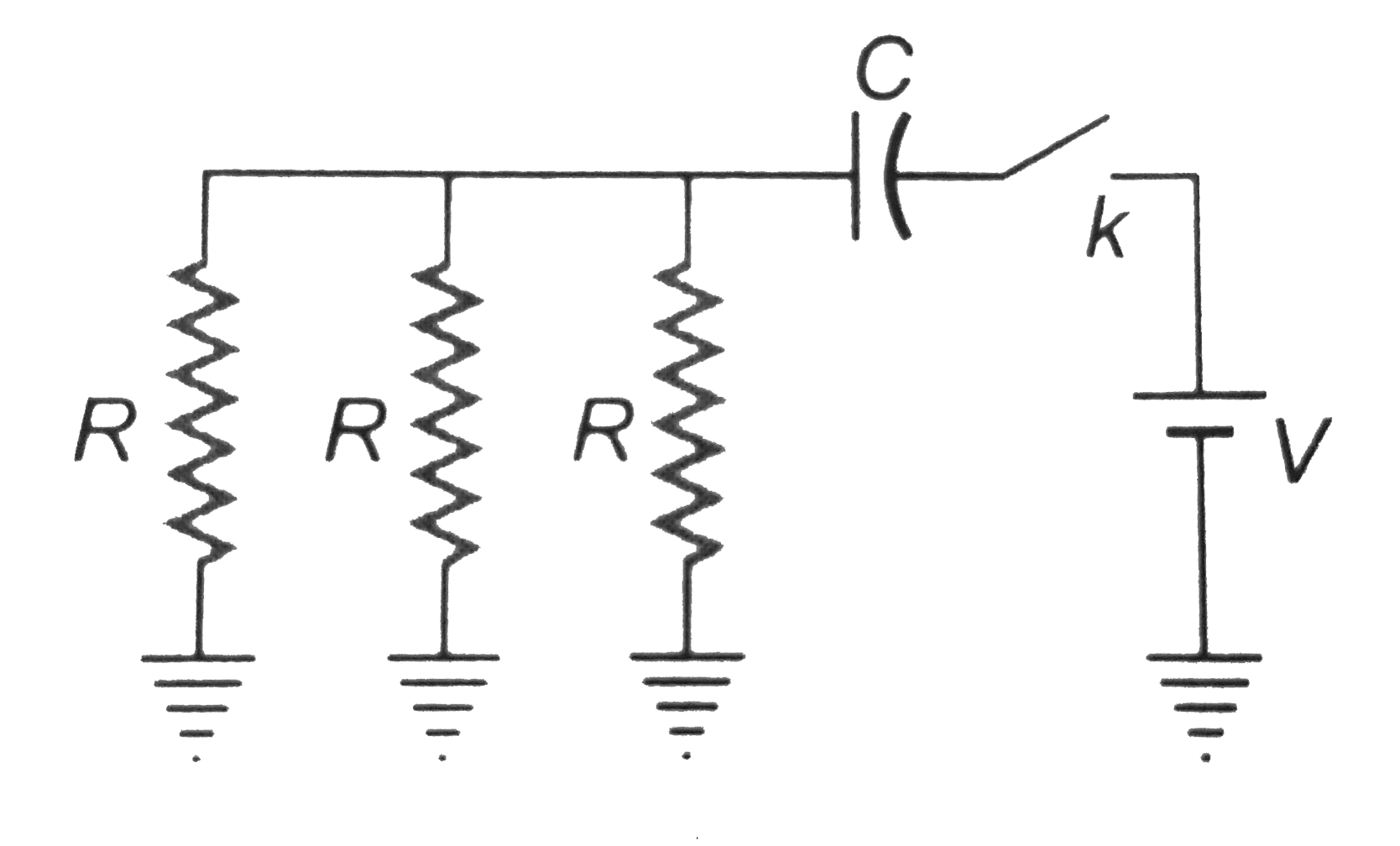
The switch shown n the figure is closed at t=0. The charge on the capacitor as a function of time is given by
 View Solution
View SolutionInitially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.
 View Solution
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionFigure shows a LCR circuit connected with a battery emf ε and internal resistance 'R'. After a long time (initially the capacitor was uncharged)
 View Solution
View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant
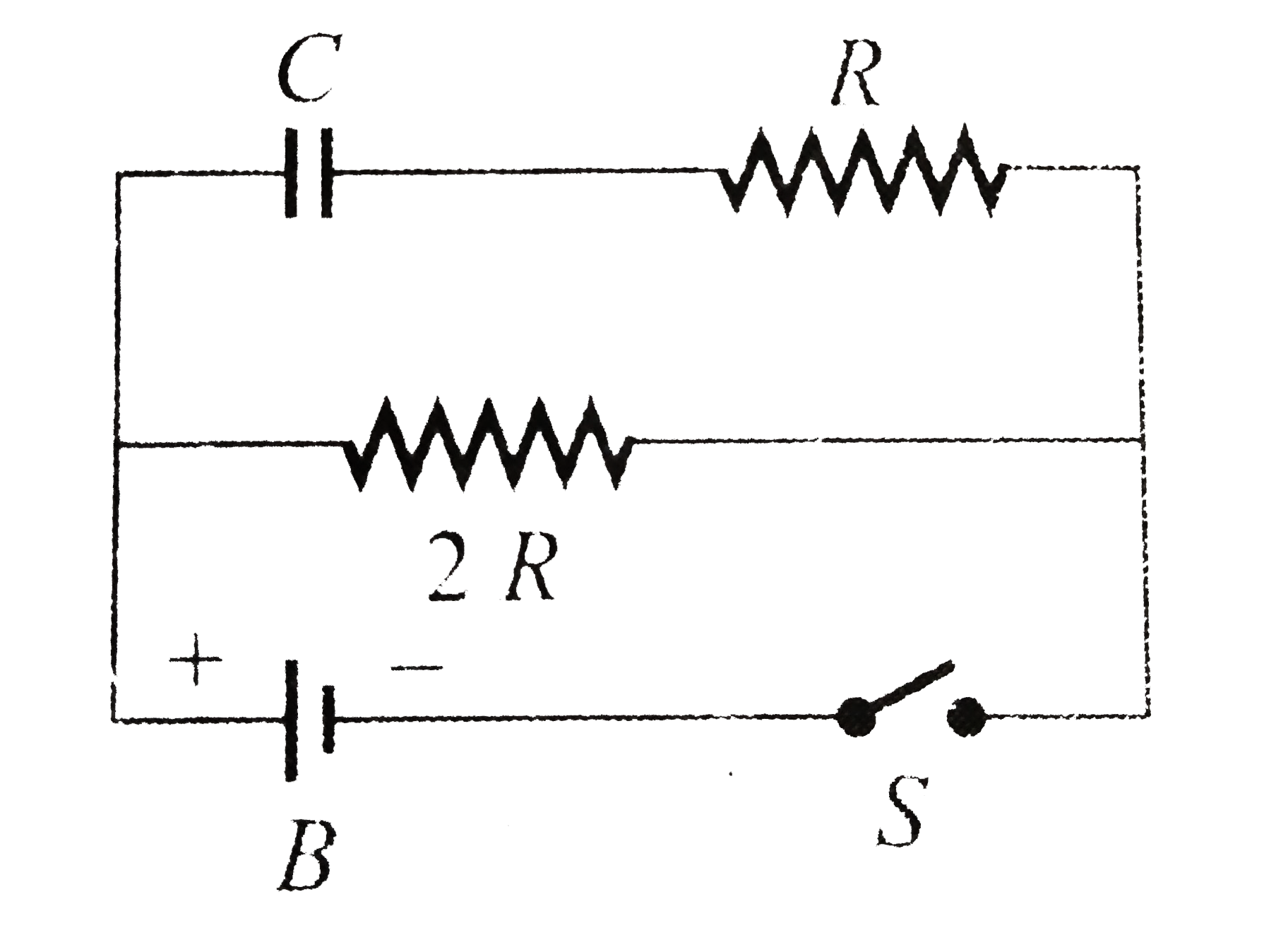 View Solution
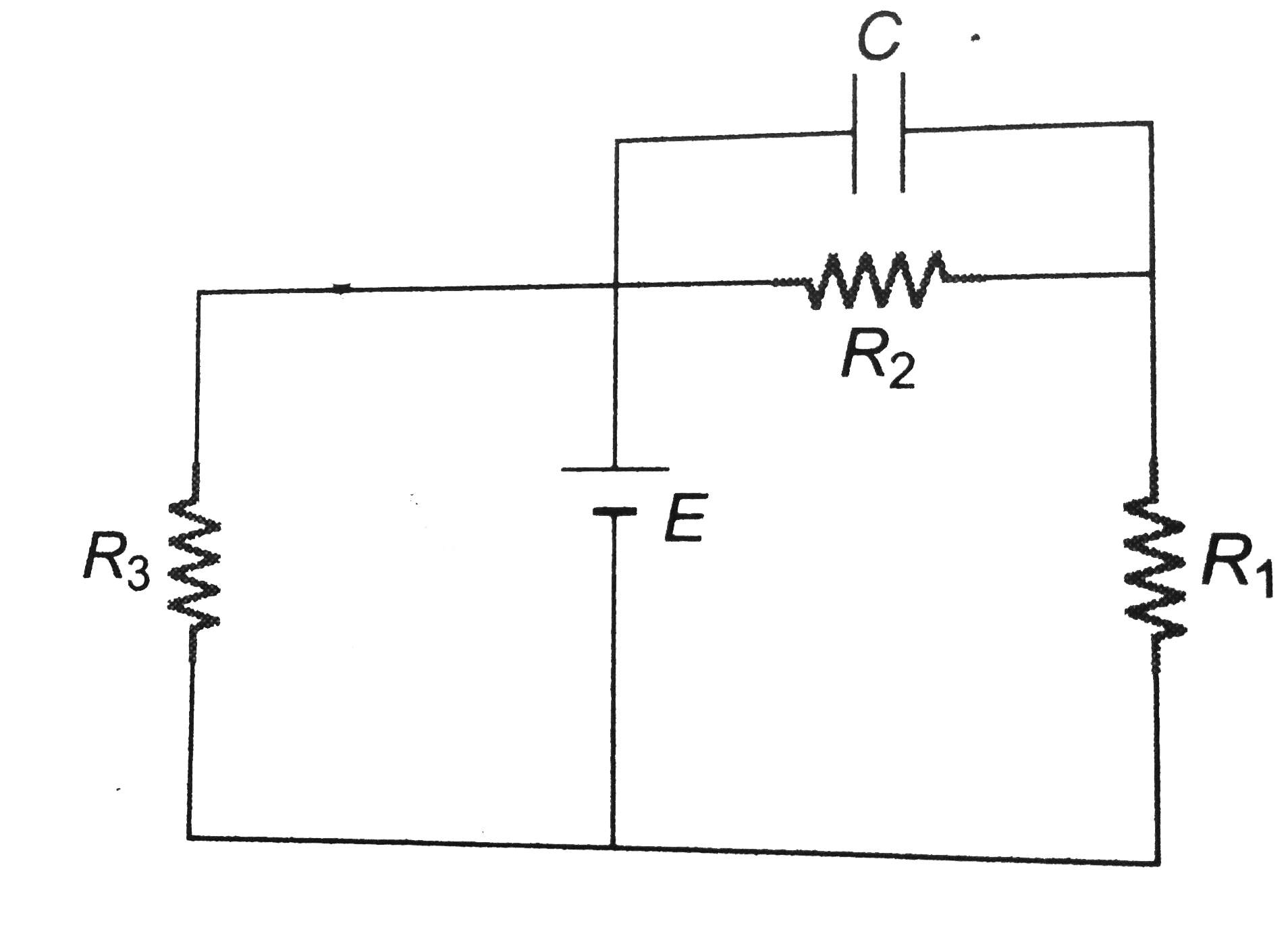
View SolutionThe charge on the capacitor is initially zero. Find the charge on the capacitor as a function of time t. All resistors are of equal value R.
 View Solution
View SolutionA capacitor of capacitance C is given a charge Q. At t=0,it is connected to an uncharged of equal capacitance through a resistance R. Find the charge on the second capacitor as a function of time.
View SolutionA capacitor having initial charge q0=CE/2 is connected to a cell of emf E through a resistor R as shown. Find the total heat generated in the circuit after the switch S is closed.
 View Solution
View SolutionA capacitor C is connected to the two equal resistances as shown in fig. What is the ratio of the time constant during charging and discharging of the capacitance?
 View Solution
View Solution

