Consider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at an angle θ . The phase difference between the ray reflected by the top surface of the glass and the bottom surface is
4πdλ(1−1n2sin2θ)1/2+π
4πdλ(1−1n2sin2θ)1/2
4πdλ(1−1n2sin2θ)1/2+π2
4πdλ(1−1n2sin2θ)1/2+2π
The correct Answer is:A
To find the phase difference between the ray reflected from the top surface of a glass slab and the ray reflected from the bottom surface, we can follow these steps:
Step 1: Understand the setup
We have a ray of light incident from air (refractive index = 1) onto a glass slab (refractive index = n) at an angle θ. The glass slab has a width d.
Hint: Visualize the situation with a diagram showing the incident ray, reflected rays, and the normal line.
Step 2: Identify the rays
When the light hits the top surface of the glass slab, part of it is reflected back (let's call this Ray 1), and part of it enters the glass slab. The ray that enters the slab will eventually reflect off the bottom surface of the slab (let's call this Ray 2) and then exit back into the air.
Hint: Remember that Ray 1 is reflected at the top surface, while Ray 2 is reflected at the bottom surface.
Step 3: Calculate the path difference
The path difference (Δp) between Ray 1 and Ray 2 can be determined by considering the geometry of the rays. The ray that enters the slab travels a distance d and then reflects back, while the reflected ray from the top surface travels a shorter distance.
The effective path difference can be expressed as:
Δp=2dcosr
where r is the angle of refraction at the glass-air interface.
Hint: Use trigonometric relationships to express cosr in terms of θ and n.
Step 4: Apply Snell's Law
Using Snell's Law, we have:
sinθ=nsinr
From this, we can derive:
sinr=sinθn
Using the identity cos2r+sin2r=1, we can find cosr:
cosr=√1−(sinθn)2
Hint: Remember that cosr can also be expressed in terms of n and θ.
Step 5: Substitute into the path difference
Now substitute cosr back into the expression for path difference:
Δp=2d√1−(sinθn)2
Hint: This expression gives you the total path difference that contributes to the phase difference.
Step 6: Calculate the phase difference
The phase difference (Δφ) between the two rays is given by:
Δϕ=2πλΔp
Substituting for Δp:
Δϕ=2πλ⋅2d√1−(sinθn)2
Step 7: Account for the phase change upon reflection
When light reflects off a medium with a higher refractive index (from air to glass), it undergoes a phase change of π (or 180 degrees). Since Ray 1 reflects off the top surface, it experiences this phase change. Ray 2 does not experience a phase change upon reflection at the bottom surface.
Thus, the total phase difference becomes:
Δϕ=4πdλ√1−(sinθn)2+π
Final Result
The final expression for the phase difference between the two rays is:
Δϕ=4πdλ√1−(sinθn)2+π
---
We have a ray of light incident from air (refractive index = 1) onto a glass slab (refractive index = n) at an angle θ. The glass slab has a width d.
When the light hits the top surface of the glass slab, part of it is reflected back (let's call this Ray 1), and part of it enters the glass slab. The ray that enters the slab will eventually reflect off the bottom surface of the slab (let's call this Ray 2) and then exit back into the air.
The path difference (Δp) between Ray 1 and Ray 2 can be determined by considering the geometry of the rays. The ray that enters the slab travels a distance d and then reflects back, while the reflected ray from the top surface travels a shorter distance.
Δp=2dcosr
where r is the angle of refraction at the glass-air interface.
Using Snell's Law, we have:
sinθ=nsinr
From this, we can derive:
sinr=sinθn
Using the identity cos2r+sin2r=1, we can find cosr:
cosr=√1−(sinθn)2
Now substitute cosr back into the expression for path difference:
Δp=2d√1−(sinθn)2
The phase difference (Δφ) between the two rays is given by:
Δϕ=2πλΔp
Substituting for Δp:
Δϕ=2πλ⋅2d√1−(sinθn)2
When light reflects off a medium with a higher refractive index (from air to glass), it undergoes a phase change of π (or 180 degrees). Since Ray 1 reflects off the top surface, it experiences this phase change. Ray 2 does not experience a phase change upon reflection at the bottom surface.
Δϕ=4πdλ√1−(sinθn)2+π
The final expression for the phase difference between the two rays is:
Δϕ=4πdλ√1−(sinθn)2+π
Topper's Solved these Questions
- WAVE OPTICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - ASSERTION & REASON CORNER
15 Videos
- WAVE OPTICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Huygens Principle
4 Videos
- WAVE OPTICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - HIGHER ORDER THINKING SKILLS
8 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle betweent the reflected and refracted rays is
A75∘B90∘C105∘D120∘
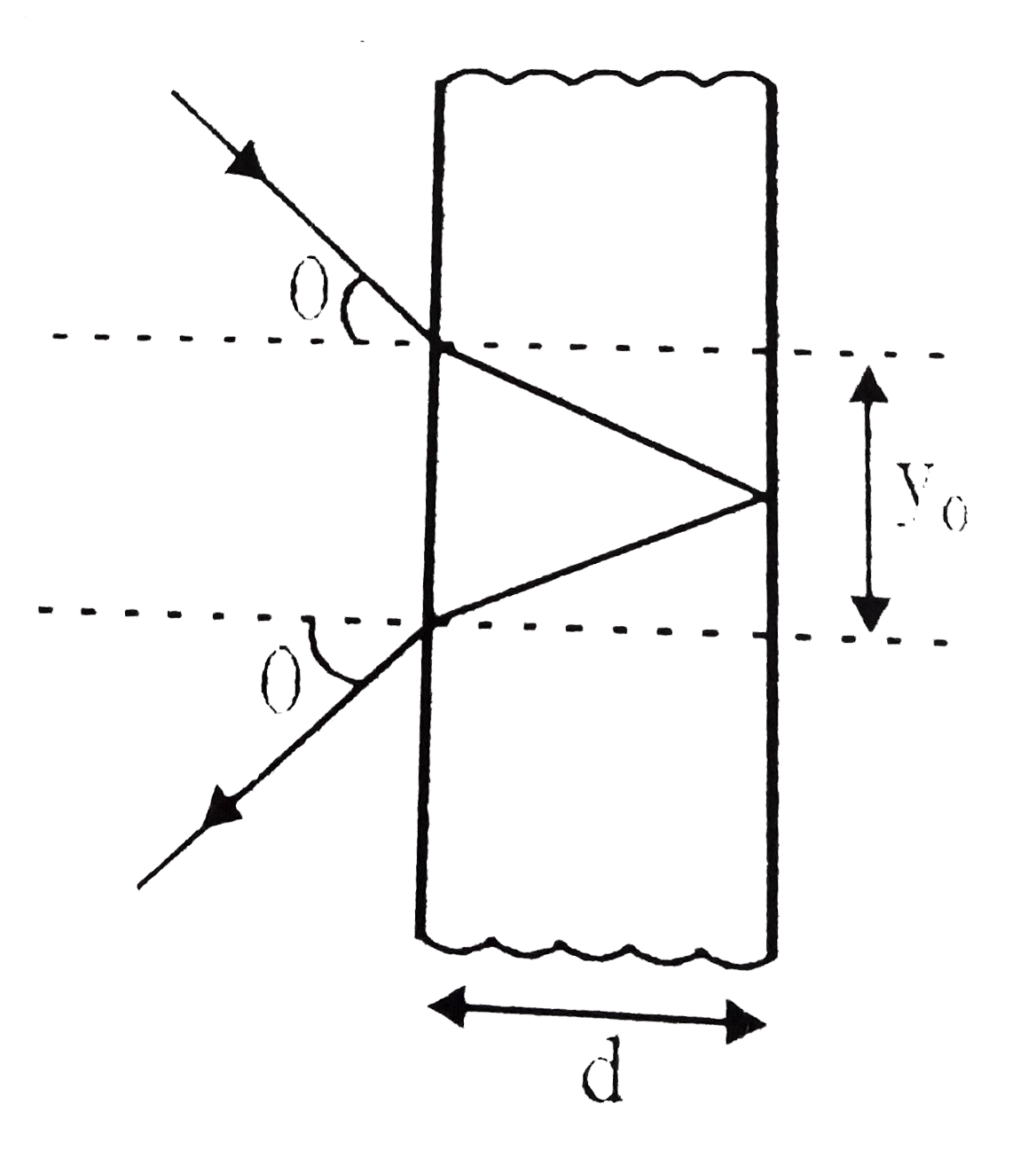
A ray of light incident from air on a glass plate of refractive index n is partly reflected and partly refracted at the two surfaces of the glass. The displacement y0 in the figure is
View SolutionA ray of light is incident on the surface of a glass plate of refractive index √3 at the polarising angle . The angle of incidence and angle of refraction of the ray is
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
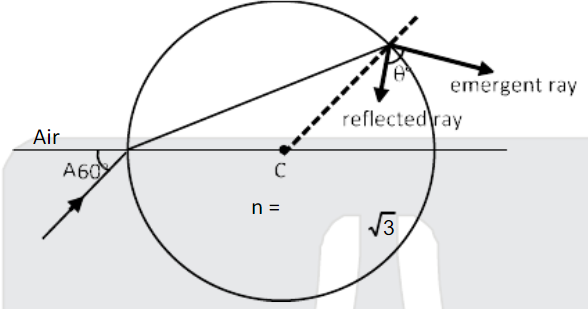
View SolutionLight incidence on a sphere of refractive index √3 placed in a air as shown in Figure. Find the angle (θ)in degree between emergent ray and reflected ray.
View SolutionA ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View SolutionA ray of light 10−9 second to cross a glass slab of refractive index 1.5. The thickness of the slab will be
View Solution
