Consider a regular tank of size (l×b) filled with a liquid of density ρ to a height H as shown in figure. Find the force at the base and on the wall of the tank.

Whenever a liquid comes in contact with solid boundaries it exerts a force on it. the force on the boundary may be obtained by integrating the pressure over the entire area of the boundary. The variations of liquid pressure acting at the base and at the wall the shown in figure a and b respectively.
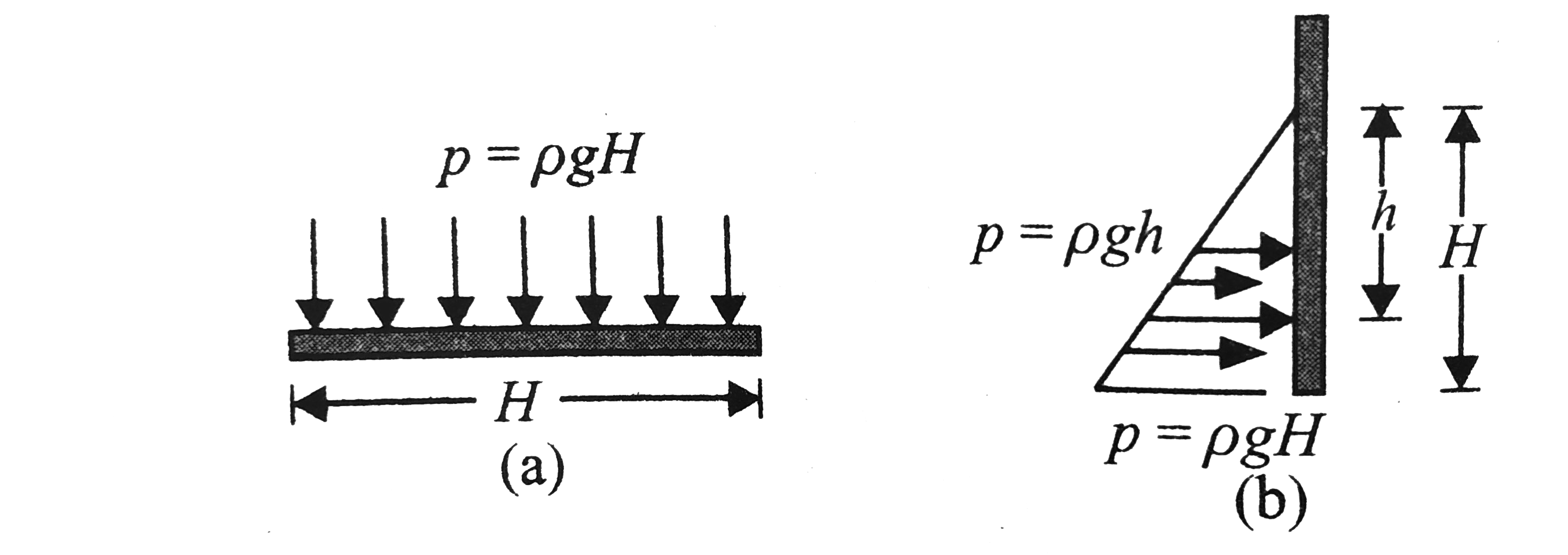
1. Force at the base: Since the pressure is uniform at the base, force acting the base is given by
F=ρ× (area of the base)
since p=ρH, therefore
F=ρghH(lb)=ρg(lbH)
Since lbH=V (volume of the liquid) so
F=ρgV= weight of the liquid inside the tank
2. Force acting on the vertical wall: Pressure acting on the vertical wall is not uniform but increases linearly with depth, pressure at a depth h from the free is p−ρgh.
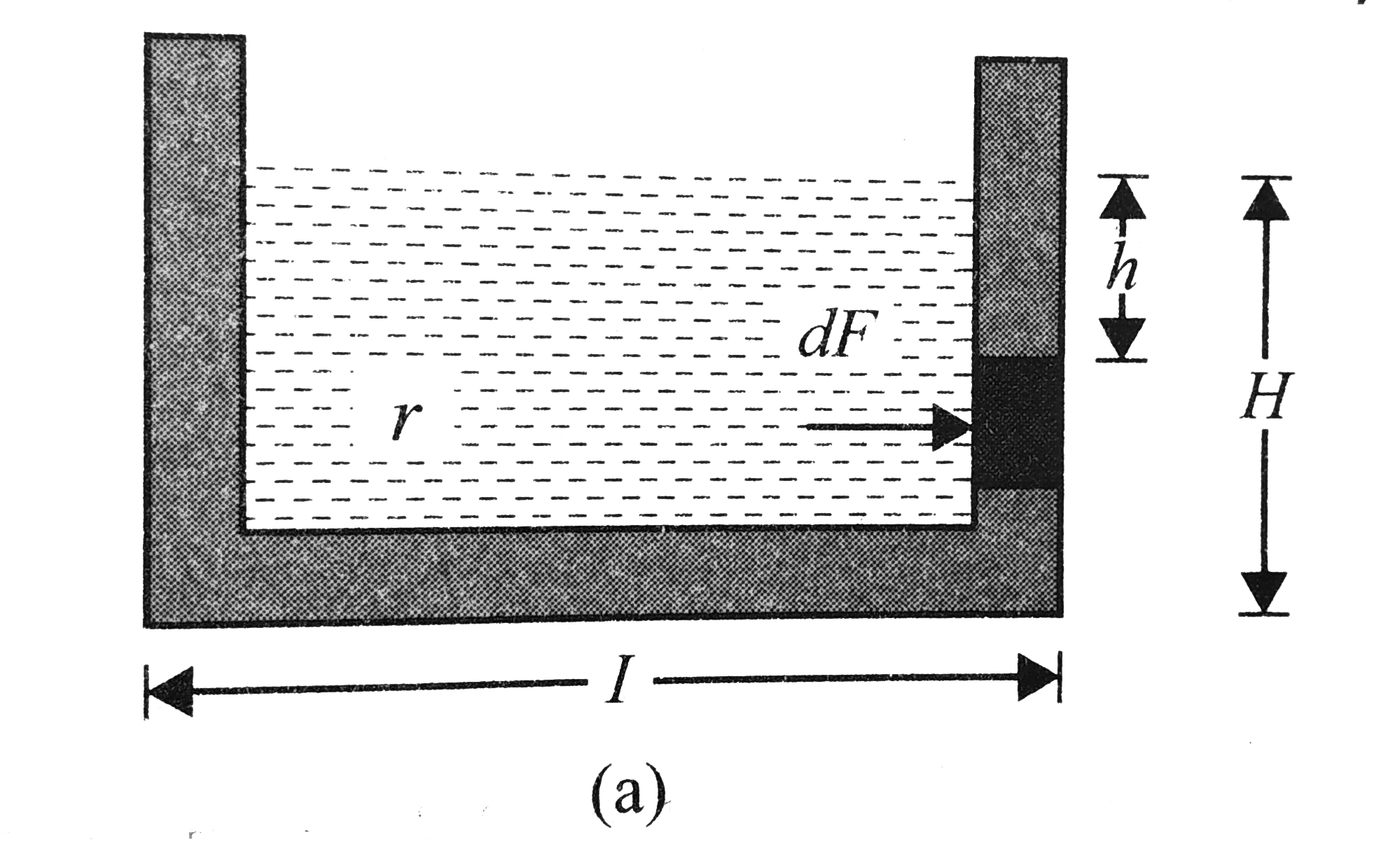
Force dF acting on a diferential element of height dh is
dF=p(bdh)=(ρgh)(bdh)=ρghdh
The total force is
F=ρgh∫H0hdh=12ρgbH2
The total force acting per unit width of the vertical wall is Fb=12ρgH2
The point of application (or the centre of force) of the total force form the free surface is given by hC=1R∫h0
Here ∫H0hdF=∫H0h(ρgpohdh)=ρgb∫H0h3dh=13ρgbH
F=12ρgbH62=→hC=23H
The total force acts at a depth 23H from the force diagram.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
7 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.1
11 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
_S01_055_Q01.png)
A cuboid (a×a×2a) is filled with two immiscible liquid of density 2ρ&ρ as shown in the figure. Neglecting atmospheric pressure ratio of force on base & side wall of the cuboid is
(a). 2:3
(b). 1:3
(c). 5:6
(d). 6:5
View SolutionA tank of square cross-section of each side is filled with a liquid of height h . Find the thrust experienced by the vertical surfaces and bottom surface of the tank.
View Solution
Knowledge Check
A beaker is filled with a liquid of density ρ upto a height h If the beaker is at rest, the mean pressure at the walls is:
A0BhρgChρg3D2hρgA cone of radius R and height H, is hanging inside a liquid of density ρ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
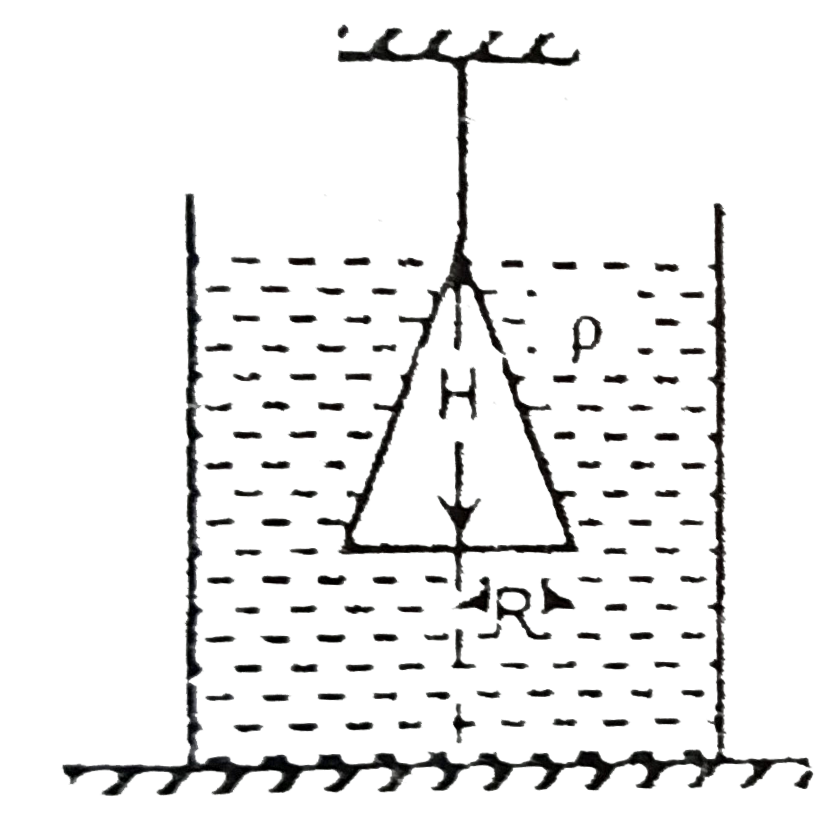 AρπgHR2BπρgHR2C43πρgHR2D23πρgHR2
AρπgHR2BπρgHR2C43πρgHR2D23πρgHR2A wooden cylindrical of diameter 4r, height h and density ρ/3 is kept on a hole of diameter 2r of a tank , filled with water of density ρ as shown in the figure . The height of the base of cylinder from the base of tank is H .
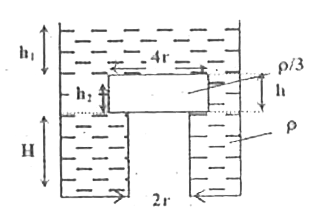
Let the cylinder is prevented from moving up , by applying a force and water level is further decreased . Then , height of water level (h2 in figure ) for which the cylinder remains in original position without application of force isAh/3B4h/9C2h/3Dh
The force F needed to support the liquid of density ρ and the vessel on it, in figure, is
View SolutionA wooden ball of density σ is released from the bottom of a tank which is filled with a liquid of density ρ(ρ>σ)up to a height h1. The ball rises in the liquid, emerges from its surface and attains a height h2 in air.If viscous effects are neglected,the ratio h2h1 is
View Solution
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level h2 (in situation 2), for which the block remains in its origin) position whithout the application of any external force
View SolutionA tank has a small hole on its side at a height y1. It is filled with a liquid (density ρ) to a height y2. If the absolute pressure at the top of the fluid is Pt, find the velocity with which it leaves the tank. Assume that the cross-sectional area of the tank is larger as compared to that of the hole.
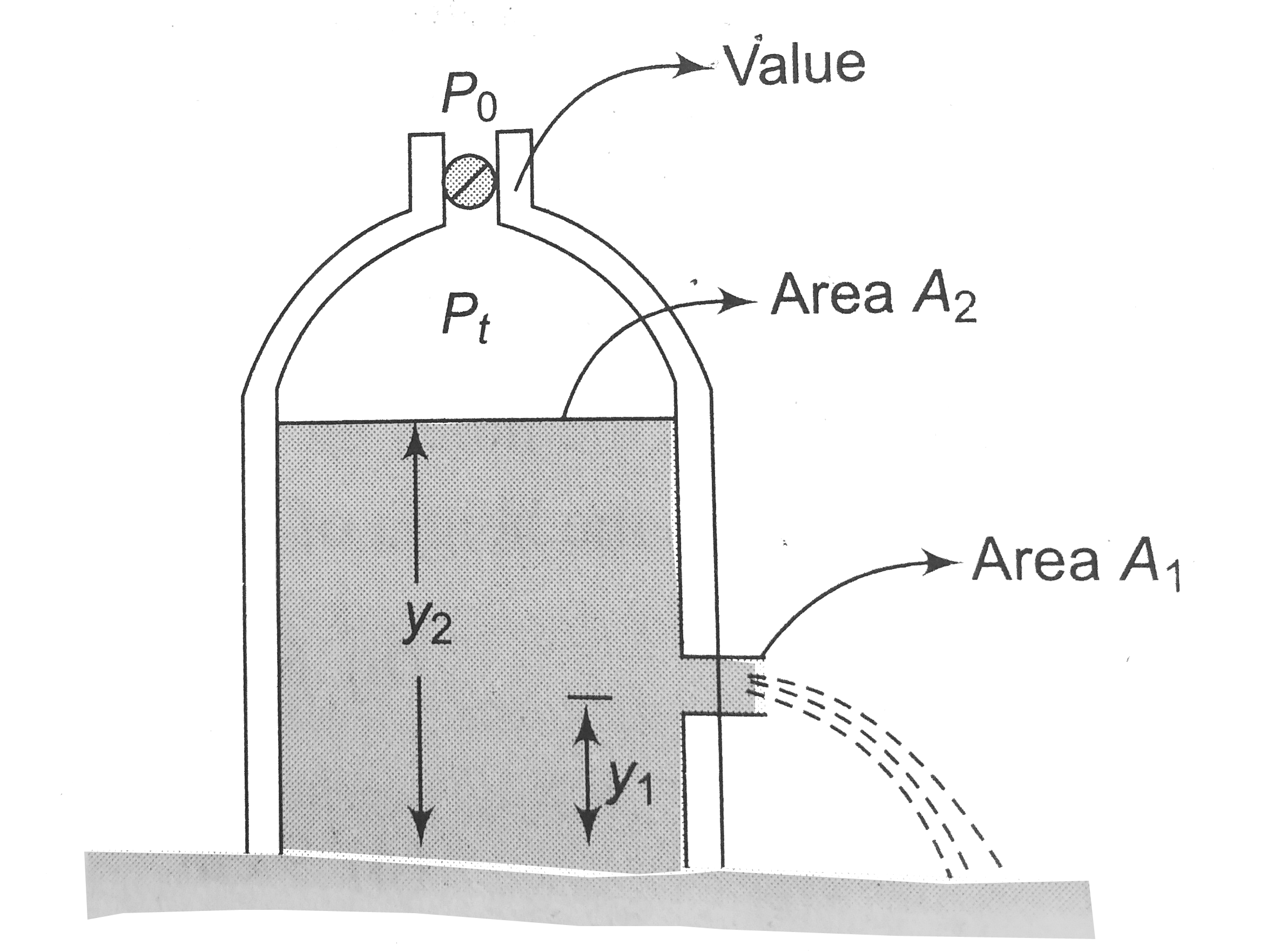
View Solution
