Consider a rubber ball freely falling from a height h = 4.9 m on a horizontal elastic plate. Assume that the duration of collision is negligible and the collision with the plate is totally elastic. Then the velocity as a function of time and the height as a function of time will be:
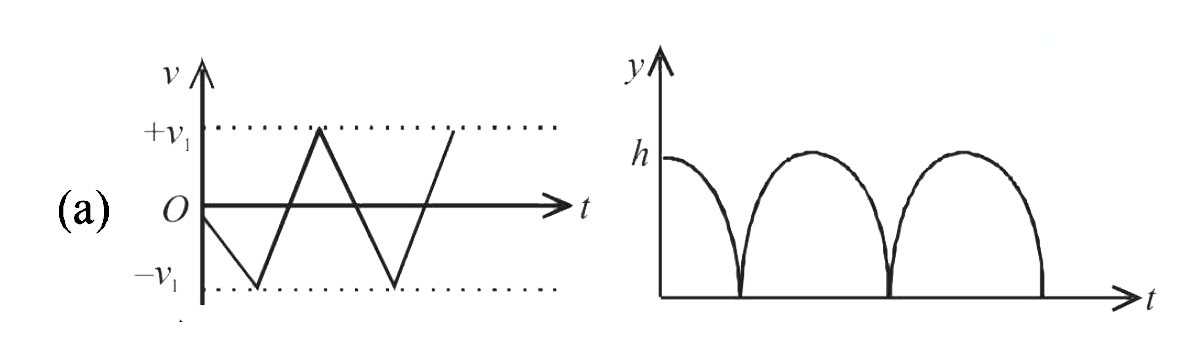


The correct Answer is:B
For downward motion v=−>
The velocity of the rubber ball increases in downward direction and we get a straight line between vandt with a negative slope .
Also applying y−y0=ut+12at2
we get y−h=−12>2⇒y=h−12>2
The graph between yandt is a parabola with y=h at t=0 . As time increases y decreases.
For upward motion .
The ball suffer elastic collision with the horizontal elastic plate therfore the direction of velocity is reversed and the magnitude remains the same . Here, v=u−> where u is the velocity just after collision . As t increases , v decreases . We get a straight line between vandt with negative slope .
Also y=ut−12>2
All these characteristics are represented by graph (b).
Topper's Solved these Questions
Similar Questions
A ball falls from a height 20m on to a horizontal plane and rebound to a height of 5/64m after 4 collisions.Find the coefficient of restitution.
View SolutionA ball falls from a height of 5m on to a horizontal plane.If the coefficient of restitution is 0.4, the height to which it rebounds after 2 collisions is approximately
View Solution
Knowledge Check
A ball after freely falling from a height of 4.9m strikes a horizontal plane. If the coefficient of restitution is 34, the ball will strike second time with the plane after
A12sB1sC32sD34sA plastic ball falling from a height 4.9m rebounds number of times. If total time for second collision is 2.4sec, then coefficient of restitution is
A0.3B0.4C0.7D0.6A ball starts falling freely from a height h from a point on the inclined plane forming an angle α with the horizontal as shown. After collision with the incline it rebounds elastically off the plane. Then it again strikes the incline at
 At=√8hg after it strikes the inclined at ABt=√2hgafter it strikes the inclined at A.Ca distance 4h sin α from A along the inclineDa distance 8h sin α from A along the incline
At=√8hg after it strikes the inclined at ABt=√2hgafter it strikes the inclined at A.Ca distance 4h sin α from A along the inclineDa distance 8h sin α from A along the incline
A rubber ball dropped from a height of 20m(g=10ms2) falls on the roof of an elevator going up at 2m/s. If the collision of the ball with the elevator is elastic, the ball rebounds with a velocity of?
View SolutionA rubber ball dropped from a height of 20m (g=10ms2) falls on the roof of an elevator going up at 2m/s .If the collision of the ball with the elevator is elastic, the ball rebounds with a velocity of
View SolutionA steel ball of mass 0.5 kg is dropped from a height of 4 m on to a horizontal heavy steel slab. The collision is elastic and the ball rebounds to its original height.
Calculate the impulse delivered to the ball during impact.
View SolutionA metal ball falls from a height of 1m on to a steel plate and jumps upto a height of 81 cm. The coefficient of restitution of the ball and steel plate is
View SolutionA ball falls from a height of 10m on to a horizontal plane. If the coefficient of restitution is 0.4, then the velocity with which it rebounds from the plane after second collision is
View Solution
