Consider a spherical gaseous cloud of mass density ρ(r) in a free space where r is the radial distance from its centre. The gaseous cloud is made of particle of equal mass m moving in circular orbits about their common centre with the same kinetic energy K. The force acting on the particles is their mutual gravitational force. If ρ(r) is constant with time. the particle number density n(r)=ρ(r) /m is : (g =universal gravitational constant)
Kπr2m2G
K6πr2m2G
3Kπr2m2G
K2πr2m2G
The correct Answer is:D
Step by step video, text & image solution for Consider a spherical gaseous cloud of mass density rho(r) in a free space where r is the radial distance from its centre. The gaseous cloud is made of particle of equal mass m moving in circular orbits about their common centre with the same kinetic energy K. The force acting on the particles is their mutual gravitational force. If rho(r) is constant with time. the particle number density n(r)=rho(r) /m is : (g =universal gravitational constant) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - COMPETITION FILE ( C. Multiple Choice Questions)
12 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - COMPETITION FILE ( D (Multiple Choice Questions))
8 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - COMPETITION FILE (JEE (Main) & Other State Boards for Engineering Entrance )
15 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
Similar Questions
Two particles of equal mass m0 are moving round a circle of radius r due to their mutual gravitational interaction. Find the time period of each particle.
View SolutionA solid sphere of radius R has a mass distributed in its volume of mass density ρ=ρ0 r, where ρ0 is constant and r is distance from centre. Then moment of inertia about its diameter is
View Solution
Knowledge Check
The kinetic energy K of a particle moving along a circle of radius R depends upon the distance s as K=as2. The force acting on the particle is
A(a) 2as2RB(b) 2as[1+s2R]1/2C(c) 2asD(d) 2aThe kinetic energy K of a particle moving along a circle of radius R depends on the distance covered a as K=as2. The force acting on the particle is
A2as2/RB2as[1+(s2/R2)]1/2C2asD2aR2/sThree particles of equal mass M each are moving on a circular path with radius r under their mutual gravitational attraction. The speed of each particle is
A√GM√2RB√GM√3RC√GM2RD√GM3R
A particle of mass m is located outside a uniform sphere of mass M at a distance r from its centre. Find:
(a) the potential energy of gravitational interaction of the particle and the sphere,
(b) the gravitational force which the sphere exerts on the particle.
View SolutionA particle of mass m moves along a circle of 'R'. The modulus of the average vector of force acting on the particle over the distance equal to a quarter of the circle is :
View SolutionA paticle of mass m is executing uniform circular motion on a path of radius r. If p is the magnitude of its linear momentum, then the radial force acting on the particle is
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionFour masses 'm' each are orbitinting in a circular of radius r in the same direction under gravitational force. Velocityof each particle is
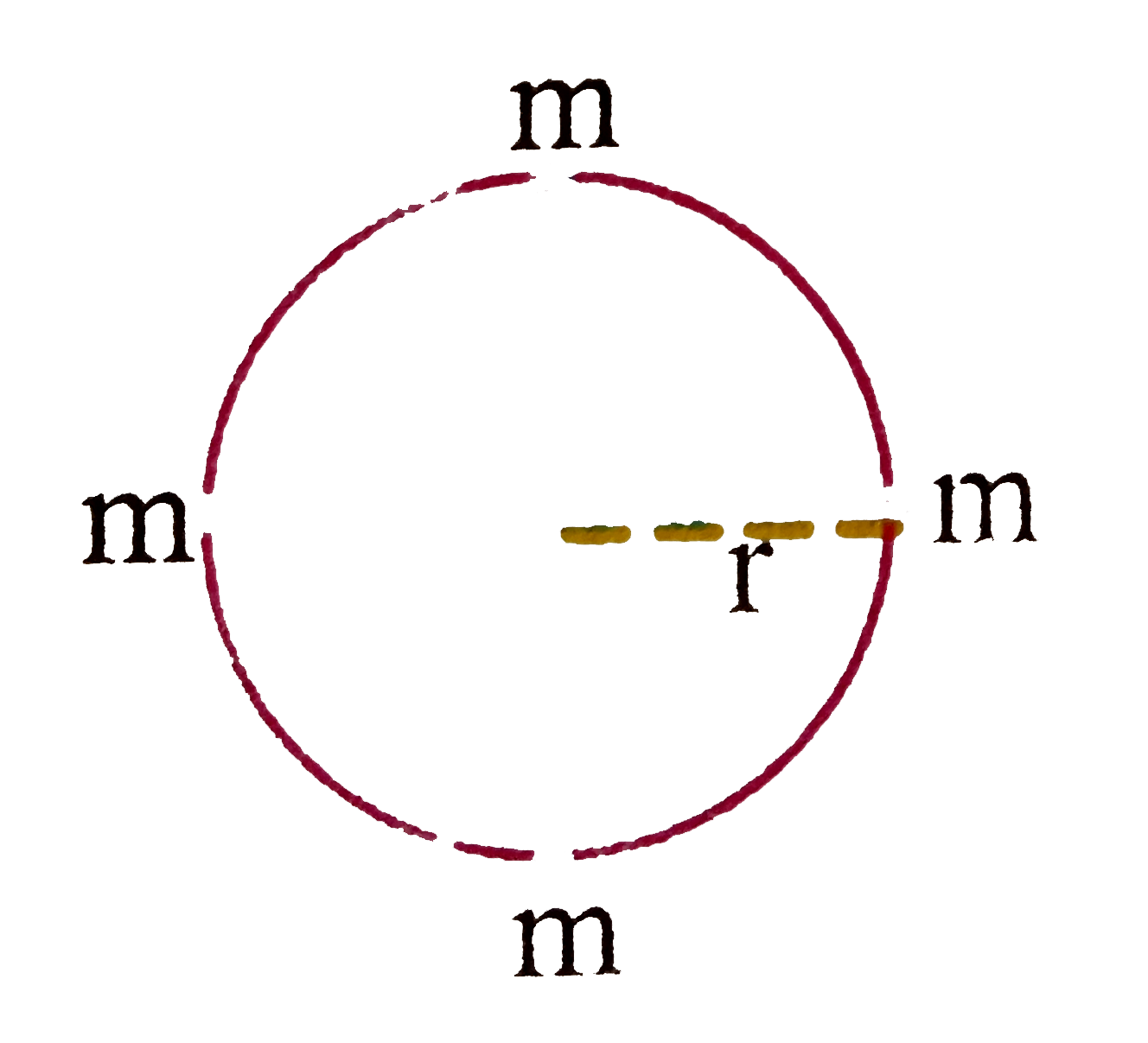
View Solution
