Consider a thin square plate floating on a viscolas liquid in a large tank. The heighth of the liquid in the tank is much less than the width of the tank. The floating plate is pulled horizontally with a constant velocity u0. Which of the following statements is (are) true?
The resistive force of liquid on the plate is inversely proportional to h
The resistive force of liquid on the plate is independent of the area of the plate
The tangential (shear) stress on the floor of the tank increases with u0
The tangential (shear) stress on the plate varies linearly with the viscosity η of the liquid
The correct Answer is:A, C, D
To solve the problem, we will analyze the situation step by step based on the principles of fluid mechanics, particularly focusing on Newton's law of viscosity.
1. Understand the Setup:
- We have a thin square plate floating on a viscous liquid in a large tank.
- The height of the liquid (H) is much less than the width of the tank.
- The plate is being pulled horizontally with a constant velocity u0.
2. Identify the Forces Acting on the Plate:
- As the plate moves, it experiences a resistive viscous force Fv from the liquid, which opposes its motion.
3. Apply Newton's Law of Viscosity:
- According to Newton's law of viscosity, the viscous force can be expressed as:
Fv=μ⋅A⋅ΔvΔy
- Where:
- μ is the dynamic viscosity of the fluid,
- A is the area of the plate,
- Δv is the change in velocity (from 0 at the bottom layer to u0 at the plate),
- Δy is the distance between the plate and the bottom layer (which is h).
4. Calculate the Viscous Force:
- From the above equation, substituting Δv=u0 and Δy=h:
Fv=μ⋅A⋅u0h
5. Analyze the Statements:
- Statement 1: The resistive force of the liquid on the plate is inversely proportional to h.
- True, as seen from the formula Fv∝1h.
- Statement 2: The resistive force of the liquid on the plate is independent of the area of the plate.
- False, as Fv is directly proportional to the area A.
- Statement 3: The tangential stress on the floor of the tank increases with u0.
- True, as tangential stress τ=FvA=μ⋅u0h is directly proportional to u0.
- Statement 4: The tangential or shear stress on the plate varies linearly with viscosity η of the fluid.
- True, as τ is directly proportional to μ.
6. Conclusion:
- The true statements are:
- Statement 1: True
- Statement 2: False
- Statement 3: True
- Statement 4: True
Final Answer:
The true statements are 1, 3, and 4.
- We have a thin square plate floating on a viscous liquid in a large tank.
- The height of the liquid (H) is much less than the width of the tank.
- The plate is being pulled horizontally with a constant velocity u0.
- As the plate moves, it experiences a resistive viscous force Fv from the liquid, which opposes its motion.
- According to Newton's law of viscosity, the viscous force can be expressed as:
Fv=μ⋅A⋅ΔvΔy
- Where:
- μ is the dynamic viscosity of the fluid,
- A is the area of the plate,
- Δv is the change in velocity (from 0 at the bottom layer to u0 at the plate),
- Δy is the distance between the plate and the bottom layer (which is h).
- From the above equation, substituting Δv=u0 and Δy=h:
Fv=μ⋅A⋅u0h
- Statement 1: The resistive force of the liquid on the plate is inversely proportional to h.
- True, as seen from the formula Fv∝1h.
- Statement 2: The resistive force of the liquid on the plate is independent of the area of the plate.
- False, as Fv is directly proportional to the area A.
- Statement 3: The tangential stress on the floor of the tank increases with u0.
- True, as tangential stress τ=FvA=μ⋅u0h is directly proportional to u0.
- Statement 4: The tangential or shear stress on the plate varies linearly with viscosity η of the fluid.
- True, as τ is directly proportional to μ.
- The true statements are:
- Statement 1: True
- Statement 2: False
- Statement 3: True
- Statement 4: True
The true statements are 1, 3, and 4.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (D. MCQ Based On A Given Passage/Comprehension)
16 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (Assertion Reason Type Questions)
11 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (JEE (Advanced) For IIT Entrance)
14 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
Two solid spheres of same size, of one iron and other of copper, are suspended by strings and submaerged in a beaker containing a certain liquid (the density of liquid is less than that of both iron and copper). If the density of copper is greater than that of iron, which of the following statements are true?
(a) The upthrust on copper sphere is greater than that on the iron sphere.
Upthrust is equal on both spheres.
(c) Tension in the string supporting copper sphere is greater than that in the string supporting iron sphere.
(d) Tension in both the strings is equal.
View SolutionThe length of a rectangle is reduced by 20% and breadth is kept constant, and the new figure that is formed is a square. Consider the following statements: The area of square is 25% less than the area of rectangle. The perimeter of square is approximately 11% less than the perimeter of rectangle. The diagonal of square is approximately 12% less than the diagonal of rectangle. Which of the statements given above is/are correct? (a) 1 only (b) 1 and 2 (c) 2 and 3 (d) 1, 2 and 3
View Solution
Knowledge Check
Consider a thin square plate floating on a viscous liquid in a large tank. The height h of the liquid in the tank is much less than the width of the tank. The floating plate is pulled horizontally with a constant velocity u0. Which of the following statement is (are) true ?
AThe resistive force of liquid on the plate is inversely proportional to hBThe resistive force of liquid on the plate is independent of the area of the plateCThe tangential (shear) stress on the floor of the tank increases with u0Dthe tangential (shear) stress on the plate varies linearly with the viscosity η of the liquidLarge number of stones are placed in a small boat. The boat is floating in a water tank. If stones are unloaded in the water in the tank then which of the following are incorrect.
ALevel of water will fallBLevel of water will riseCWater level falls at first and then risesDWater level remains unchangedA flat plate is moving normal to its plane through a gas under the action of a constant force F. The gas is kept at a very low pressure. The speed of the plate v is much less than the average speed u of the gas molecules. Which of the following options is/are true?
AThe pressure difference between the leading and trailing faces of the plate is proportional to uvBAt a later time the external force F balances the resistive forceCThe resistive force experienced by the plate is proportional to vDThe plate will continue to move with constant non-zero acceleration, at all times
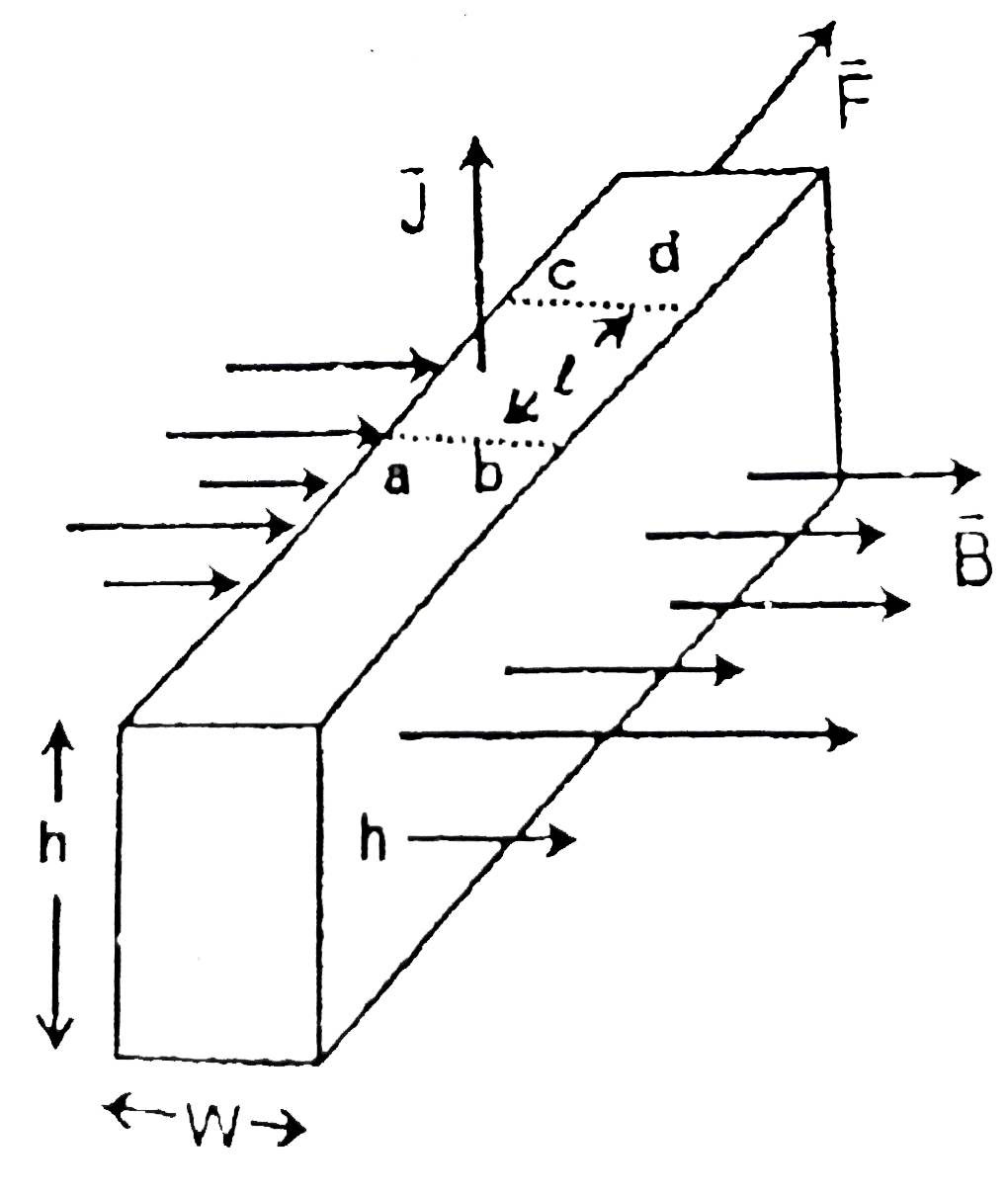
Magnetic forces acting on conducting fluids provide a convenient means of pumping these fluids. For example, this method can be used to pump blood without damage to the cells that can be caused by a mechanical pump. A horizontal tube with rectangular cross section (height h, width W) is placed at right angles to a uniform magnetic field with magnitude B so that a length l is in the field (see figure). The tube is filled with conducting liquid and an electric current density J is maintained in the third mutually perpendicular direction.
Which of the following statement is true ?
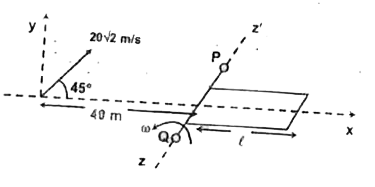
View SolutionA ball is projected with velocity of 20√2 m/s at angle of 45∘ with horizontal and at the same instant another plate is rotating with constant angular velocity ω(ω=π/4rad/sec) in vertical plane as shown in the figure. If the mass of the plate is much larger than the mass of the ball, the plate is initially in horizontal position and collision is perfectly elastic, then choose the correct statement(s)
View SolutionA tube of length 'L' is filled completely with an in compressiblem liquid of mass 'M' and closed at both ends. The tube is then rotated in a horizontal plane about one of it's ends with a uniform angular velocity 'ω'. Then which of following statements are true :
View SolutionA block with mass (M) is connected by a massless spring with stiffness constant (k) to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude A about an equilibrium position (x_0). Consider two cases : (i) when the block is at (x_0) , and (ii) when the block is at x=x0+A. In both the cases, a particle with mass m(lt M) is softly placed on the block after which they strick to each other. Which of the following statement (s) is (are) true about the motion after the mass (m) is placed on the mass (M) ?
View SolutionCertain words are printed in blod to help you to locate -them while answering some of the questions .
Though the U.S. prides itself on being a leader in the world community, a recent report shows that it lags far behind other industrialised countries in meeting the needs of its youngest and most vulnerable citizens. The US. has a higher Infant mortality rate, a higher proportion of low birth weight babies, a smaller proportion of babies immunised against chilhood diseases and a much higher rate of adolescent pregnancies. These findings, described as a "quier crisis" requiring immediate and far-reaching action, appeared in a report prepared by a task force of educators, doctors, politicians and business people. According to the report, a fourth of the nation's 12 million infants and toddlers live in poverty. As many as half confront risk factors that could harm their ability to develop intellectually, physically and socially. Child immunisations are too low, more children are born into property, more are in substandard carewhile their parents. Work and more are being raised by single lead to educational and health problems that are much harder and more costly to reverse.
The crisis begins in the womb with unplanned parenthood. Women with unplanned pregnancies are less likely to seek prenatal care. In the U.S. 80% of teenage pregnancies and 56% of all pregnancies are unplanned. The problems continue after birth where unplanned pregnancies and unstable partnerships often go hand in hand. Since 1950, the numcent of all births today are to unmarried mothers. As the number of single parent families grows and more woman enter the work force, infants and toddlers are increasingly in the care of people other than their parents. Most disturbingly, recent statistics show that American parents are increasingly neglecting or abusing their children. In only four years from 1987-1991 the number of children in foster care increased by over 50 percent. Babies under the age of one are the fastest growing category of children entering foster care. This crisis affects children under the age of three most severely, the report says Yet, it is this period from infancy through pre-school years that sets the stage for a child's future.
Which of the following statements is not true in the context of the passage ?
View Solution
