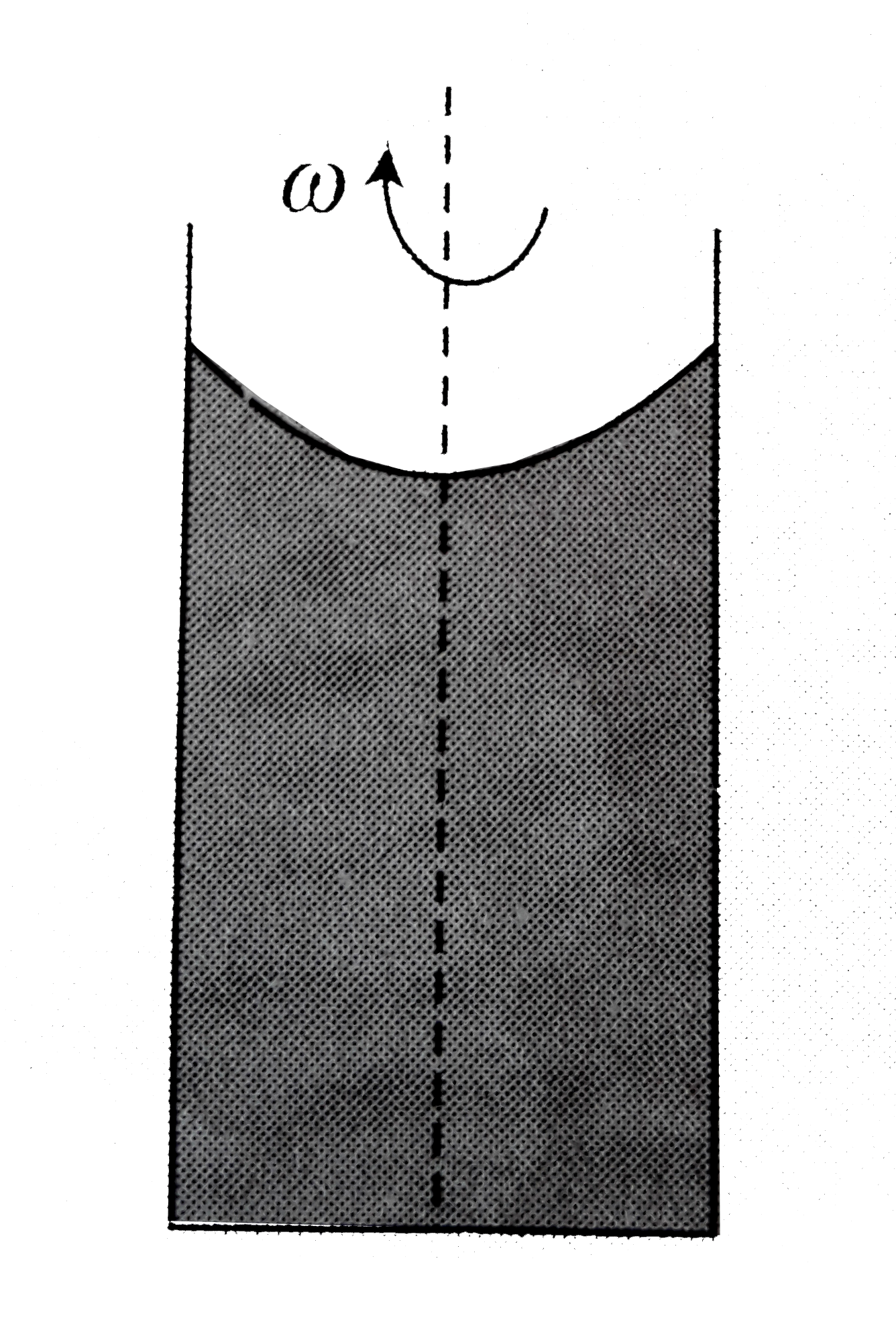
A small tank of cylindrical shape and of radius R is containing a liquid of density σ. On rotating the vessel about its axis with angular velocity ω, the liquid rises at the sides of vessel through height h. P1andP2 are pressure at sides and at the centre of tank respectively, then
P1>P2
P1=P2
P2>P1
h=R2ω22g
The correct Answer is:B, D
To solve the problem, we need to analyze the situation of a cylindrical tank filled with liquid that is rotating about its axis. The key points we need to consider are the pressure at the sides of the tank (P1) and the pressure at the center of the tank (P2), as well as the height (h) to which the liquid rises at the sides.
1. Understanding the Setup:
- We have a cylindrical tank of radius R filled with a liquid of density σ.
- The tank is rotating with an angular velocity ω.
- Due to the rotation, the liquid surface will not remain flat; instead, it will take the shape of a paraboloid, rising at the sides of the tank.
2. Defining the Height:
- Let h be the height to which the liquid rises at the sides of the tank.
- The height of the liquid at the center of the tank will be lower than at the sides.
3. Applying the Hydrostatic Pressure Equation:
- The pressure at a depth y in a liquid is given by the equation:
P=P0+σgy
- Where P0 is the atmospheric pressure, σ is the density of the liquid, g is the acceleration due to gravity, and y is the height of the liquid column above the point where pressure is being measured.
4. Pressure at the Center (P2):
- At the center of the tank (where x=0), the height of the liquid is ymin.
- Therefore, the pressure at the center P2 is:
P2=P0+σgymin
5. Pressure at the Side (P1):
- At the side of the tank (where x=R), the height of the liquid is ymax=ymin+h.
- Thus, the pressure at the side P1 is:
P1=P0+σg(ymin+h)
6. Finding the Height (h):
- From the analysis of the forces acting on a fluid element in the rotating tank, we can derive that:
h=ω2R22g
7. Comparing Pressures (P1 and P2):
- Now, substituting h into the equations for P1 and P2:
P1=P0+σg(ymin+ω2R22g)
P2=P0+σgymin
- Thus, we can see that:
P1=P2+σgω2R22g
- This shows that P1>P2.
Conclusion:
- The final results are:
h=ω2R22g
P1>P2
- We have a cylindrical tank of radius R filled with a liquid of density σ.
- The tank is rotating with an angular velocity ω.
- Due to the rotation, the liquid surface will not remain flat; instead, it will take the shape of a paraboloid, rising at the sides of the tank.
- Let h be the height to which the liquid rises at the sides of the tank.
- The height of the liquid at the center of the tank will be lower than at the sides.
- The pressure at a depth y in a liquid is given by the equation:
P=P0+σgy
- Where P0 is the atmospheric pressure, σ is the density of the liquid, g is the acceleration due to gravity, and y is the height of the liquid column above the point where pressure is being measured.
- At the center of the tank (where x=0), the height of the liquid is ymin.
- Therefore, the pressure at the center P2 is:
P2=P0+σgymin
- At the side of the tank (where x=R), the height of the liquid is ymax=ymin+h.
- Thus, the pressure at the side P1 is:
P1=P0+σg(ymin+h)
- From the analysis of the forces acting on a fluid element in the rotating tank, we can derive that:
h=ω2R22g
- Now, substituting h into the equations for P1 and P2:
P1=P0+σg(ymin+ω2R22g)
P2=P0+σgymin
- Thus, we can see that:
P1=P2+σgω2R22g
- This shows that P1>P2.
- The final results are:
h=ω2R22g
P1>P2
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (D. MCQ Based On A Given Passage/Comprehension)16videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (Assertion Reason Type Questions)11videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (JEE (Advanced) For IIT Entrance)14videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)12videos
MATHEMATICAL TOOLS
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test15videos
MOTION IN A PLANE
Similar Questions
A liquid has been poured into a cylindrical vessel. What shape will the surface of the liquid have if the vessel is rotated uniformly about its axis with an angular velocity ω ?
View SolutionA cylinder of radius R full of liquid of density p is rotated about its axis at w rad/s. The increase in pressure at the centre of the cylinder will be
View Solution
Knowledge Check
- Question 1 - Select One
A cylindrical vessel of radius r containing a liqiud is rotating about a vertical axis through the centre of circular base, If the vessel is rotating with angular velocity ω then what is the difference of the heights of liquid at centre of vessel and edge?
Arω2gBr2ω22gC√2grωDω22gr2 - Question 2 - Select One
A ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
A12mr2ω2Bmrω2Cmr2ω2D12mrω2 - Question 3 - Select One
A ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
A12mr2ω2Bmrω2Cmr2ω2D13mr2ω2
A liquid of density ρ is in a vessel rotating with angular velocity ω as shown in figure. If P0 is the atmospheric pressure, find pressure at a radial distance r from the axis.
 .View Solution
.View SolutionA non-conducting thin disc of radius R charged uniformly over one side with surface density σ, rotates about its axis with an angular velocity ω. Find (a) the magnetic field induction at the centre of the disc (b) the magnetic moment of the disc.
View SolutionA thin ring of radius R is made of a material of density ρand Young's modulus Y. If the ring is rotated about its centre in its own plane with angular velocity omega , find the small increases in its radius.
View SolutionA solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View SolutionA non-conducting thin disc of radius R and mass m having charge uniformly over one side with surface density σ rotates about its axis with an angular velocity ω. Find :
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.
( c) the ratio of magnetic moment and angular momentum of disc.View Solution

