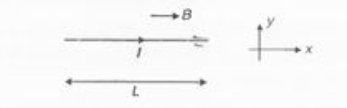
Consider a wire carrying a steady current, I placed in a uniform magnetic field →B perpendicular to its length. Consider the charges inside the wire. It is known that magnetic forces do not work. This implies that
Motion of charges inside the conductor is unaffected by B, since they do not aborb energy
some charges inside the wire move to the surface as a result of B
if the wire moves under the influence of B, no work is done by the force.
If the wire moves under the influence of B, no work is done by the magnetic force on the ions, assumed fixed within the wire.
The correct Answer is:B, D
To solve the problem, we need to analyze the situation of a wire carrying a steady current placed in a uniform magnetic field that is perpendicular to its length. We will explore the implications of the magnetic forces acting on the charges within the wire and determine the correct statements regarding the work done by these forces.
1. Understanding the Setup:
- We have a wire carrying a steady current I.
- The magnetic field →B is uniform and perpendicular to the length of the wire.
- The current flows in one direction (let's say along the positive x-axis), while the magnetic field is directed in another (let's say along the positive z-axis).
2. Identifying the Charges:
- The wire consists of charged particles (typically electrons) that move in the opposite direction to the current. Therefore, if the current is in the positive x-direction, the electrons move in the negative x-direction.
3. Calculating the Magnetic Force:
- The magnetic force →F on the wire can be calculated using the formula:
→F=I→L×→B
- Here, →L is the length vector of the wire in the direction of the current. Since →L is along the x-axis and →B is along the z-axis, the angle between them is 90 degrees. Thus, the magnetic force will be directed along the negative y-axis.
4. Analyzing the Work Done:
- Magnetic forces do not do work on the charges because the force is always perpendicular to the displacement of the charges.
- The work done W by the magnetic force is given by:
W=→F⋅→s
- Since the force →F is perpendicular to the displacement →s of the charges, the work done is zero:
W=F⋅s⋅cos(90∘)=0
5. Evaluating the Options:
- Option 1: "Motion of charges inside the conductor is unaffected by B since they do not absorb energy."
- This is incorrect because the magnetic field does affect the motion of the charges, causing them to move in circular paths.
- Option 2: "Some charges inside the wire move to the surface as a result of B."
- This is correct. The magnetic force can cause some charges to redistribute towards the surface of the conductor.
- Option 3: "If the wire moves under the influence of B, no work is done by the force."
- This is incorrect because if the wire moves, the magnetic force can do work on the wire.
- Option 4: "If the wire moves under the influence of B, no work is done by the magnetic force on the ions."
- This is correct. The ions are fixed in the wire and do not move, so no work is done on them by the magnetic force.
Conclusion:
The correct options are Option 2 and Option 4.
- We have a wire carrying a steady current I.
- The magnetic field →B is uniform and perpendicular to the length of the wire.
- The current flows in one direction (let's say along the positive x-axis), while the magnetic field is directed in another (let's say along the positive z-axis).
- The wire consists of charged particles (typically electrons) that move in the opposite direction to the current. Therefore, if the current is in the positive x-direction, the electrons move in the negative x-direction.
- The magnetic force →F on the wire can be calculated using the formula:
→F=I→L×→B
- Here, →L is the length vector of the wire in the direction of the current. Since →L is along the x-axis and →B is along the z-axis, the angle between them is 90 degrees. Thus, the magnetic force will be directed along the negative y-axis.
- Magnetic forces do not do work on the charges because the force is always perpendicular to the displacement of the charges.
- The work done W by the magnetic force is given by:
W=→F⋅→s
- Since the force →F is perpendicular to the displacement →s of the charges, the work done is zero:
W=F⋅s⋅cos(90∘)=0
- Option 1: "Motion of charges inside the conductor is unaffected by B since they do not absorb energy."
- This is incorrect because the magnetic field does affect the motion of the charges, causing them to move in circular paths.
- Option 2: "Some charges inside the wire move to the surface as a result of B."
- This is correct. The magnetic force can cause some charges to redistribute towards the surface of the conductor.
- Option 3: "If the wire moves under the influence of B, no work is done by the force."
- This is incorrect because if the wire moves, the magnetic force can do work on the wire.
- Option 4: "If the wire moves under the influence of B, no work is done by the magnetic force on the ions."
- This is correct. The ions are fixed in the wire and do not move, so no work is done on them by the magnetic force.
The correct options are Option 2 and Option 4.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOVING CHARNGES AND MAGNETISMEXERCISE - Very Short Answer Type Question5videos
MOVING CHARNGES AND MAGNETISM
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOVING CHARNGES AND MAGNETISMEXERCISE - Short Answer Type Question6videos
MOVING CHARNGES AND MAGNETISM
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOVING CHARNGES AND MAGNETISMEXERCISE - Long Answer Type Questions7videos
MOVING CHARNGES AND MAGNETISM
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - All Questions24videos
MAGNETISM AND MATTER
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - NUCLEIEXERCISE - Long answer type question10videos
NUCLEI
Similar Questions
Knowledge Check
- Question 1 - Select One
An 8 cm long wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. If the magnetic field inside the solenoid is 0.3 T, then magnetic force on the wire is
A0.14NB0.24NC0.34ND0.44N - Question 2 - Select One
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
A 3⋅0cm wire carrying a current of 10A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0⋅27T. What is the magnetic force on the wire?
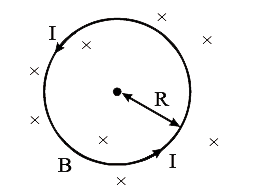
View SolutionA current (I) carrying circular wire of radius R is placed in a magnetic field B perpendicular to its plane. The tension T along the circumference of the wire is
 View Solution
View Solution(a) Write the expression for the force, →F, acting on a charged particle of charge 'q', moving with a velocity →V in the presence of both electric field →E and magnetic field →B. Obtain the condition under which the particle moves undeflected through the fields.
(b) A rectangular loop of size l×b carrying a steady current I is placed in a uniform magnetic field →B. Prove that the torque →τ acting on the loop is given by
→τ=→m×→B, where →m is the magnetic moment of the loop.View SolutionA circular flexible loop of wire of radius r carrying a current I is placed in a uniform magnetic field B . If B is doubled, then tension in the loop
View SolutionWhen a current carrying coil is placed in a uniform magnetic field with its magnetic moment anti-parallel to the field.
View SolutionWhen a current carrying coil is placed in a uniform magnetic field with its magnetic moment anti-parallel to the field.
View Solution