Consider an infinita ladder of network shown In fig 5.223A voltage is applied between points A and B. If the voltage is havled after each seciton, find the raito of

Suggest a method to terminate it after a few sections without introducing much error in its attenuation.
Voltage across AB is v, voltage acrpss A'B' os V/2
i.e., voltage across is
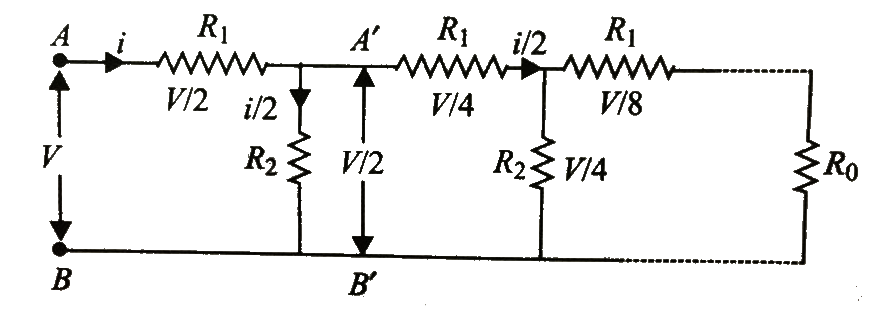
Now from Kirchhoff's law, it is obvious that voltge across is
Resistance will not be affected if equivalent resistance R
becomes independent of number of sections in the circuit. This is only possible if the terminating resistance is it self equal to equivalent resistance the equivalnet resistance
of and is
is in series with it, so equivalent resistance between A and B is
According to proposition
Solving for we get
Thus, the circuit may be terminated after a few section if
resistance is connected in parallel as shown in fig
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Single Correct72videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Multiple Correct16videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.250videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
Consider an infinite ladder of network shown In fig 5.223. A voltage is applied between points A and B. If the voltage is halved after each section, find the ratio of R1/R2.
 View Solution
View SolutionConsider an infinite ladder of network shown In fig 5.223. A voltage is applied between points A and B. If the voltage is halved after each section, find the ratio of R1/R2.
 View Solution
View SolutionIn the circuit shown in fig. 5.265, E1=E2=E3=2V and R1=R2=4Ω. The current flowing between points A and B through battery E2 is
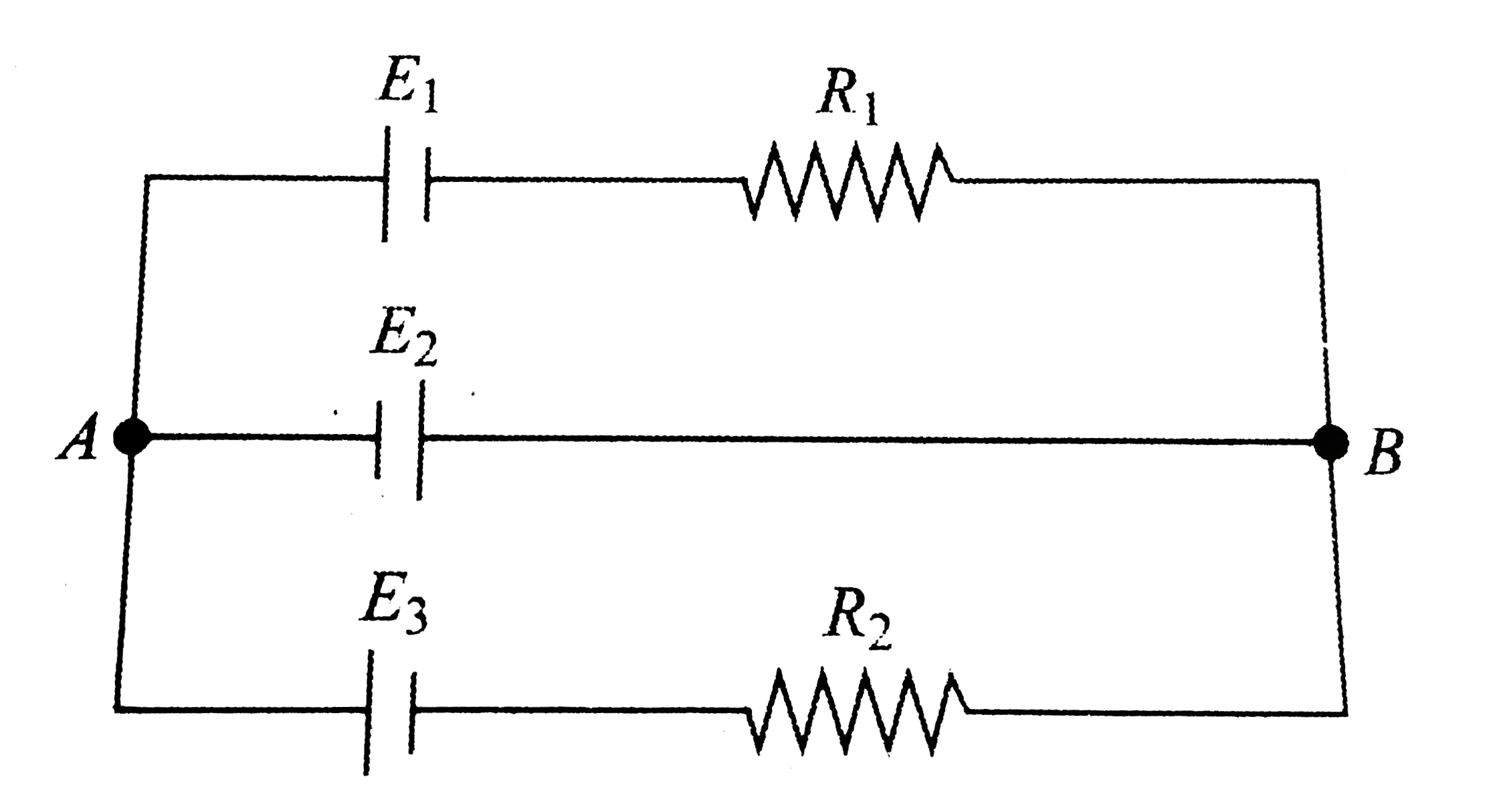 View Solution
View SolutionFind the resistance of a wire frame shaped as cube (Fig) when measured between points (a) 1.7, (b) 1.2, (c) 1.3.
The resitance of each edge of the frame is R
 View Solution
View SolutionA constant voltage V=25V is maintained between points A and B of the circuit (Fig). Find the magnitude and direction of the current flowing through the segment CD if the resistances are equal to R1=1.0Ω,R2=2.0Ω,R3=3.0Ω and R4=4.0Ω.
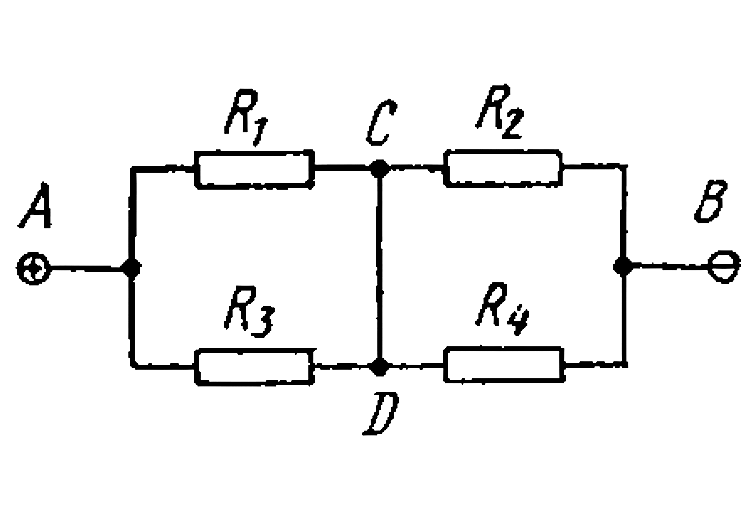 View Solution
View SolutionVariation of current passing through a conductor as the voltage applied across its ends is varied as shown in the adjoining diagram. If the resistance (R) is determined at the points A, B, C and D, we will find that
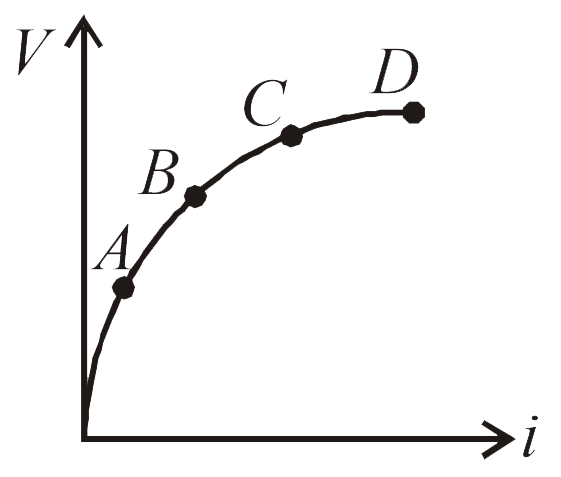 View Solution
View SolutionThe circuit diagram shwon in the fig consist of a large number of elementws (each element has two resistors R1andR2. The resistance of the resistors in each subsequent element differs by a factor of k=12 from the resistance of the resistors in previous elements find the equivalent resistance between A and B shown in
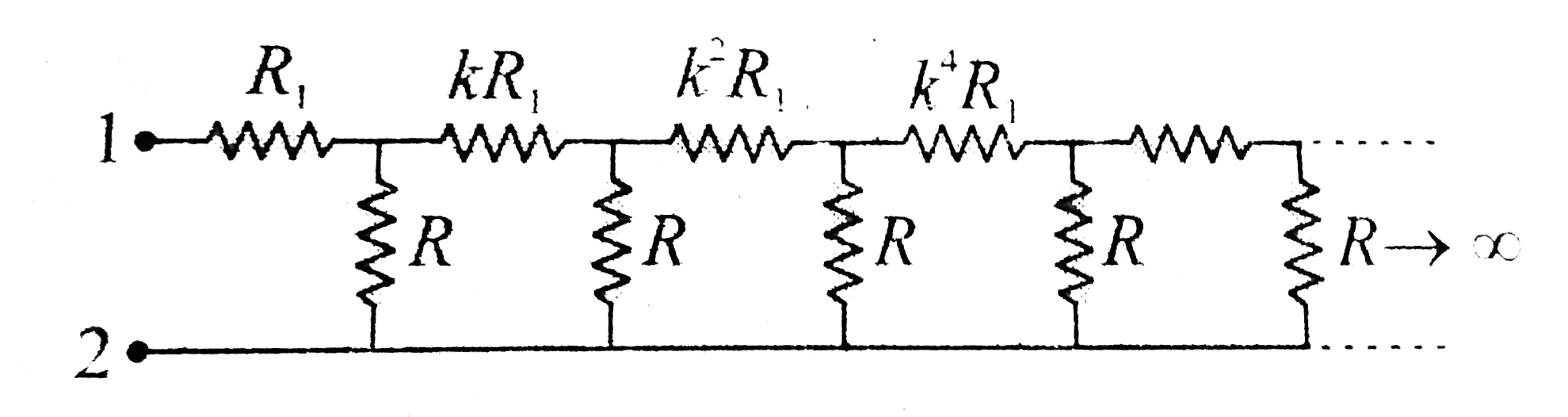 View Solution
View SolutionEach component in the infinite network shwon in fig has a resistance R=4Ω. A battery of emf1 V and neglibible interanal resistance is connected between any two neighboring points, say X and Y.
i. Find current shown by the ammeter.
ii. if the resistance R between X and Y is removed , then find current shown by ammeter.
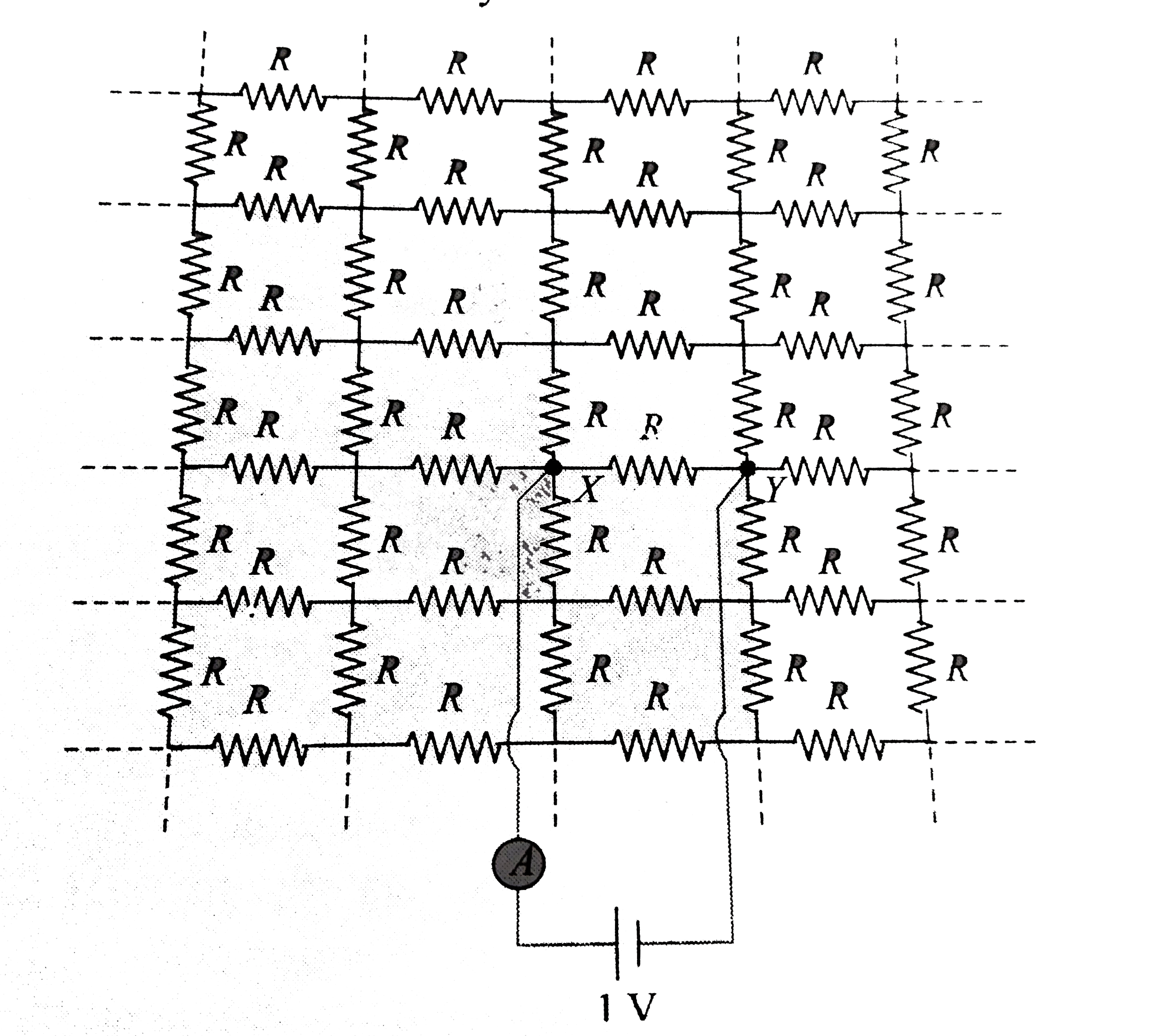 View Solution
View SolutionConsider a block of conducting material of resistivity 'ρ' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage ΔV developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E=ρj, where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.
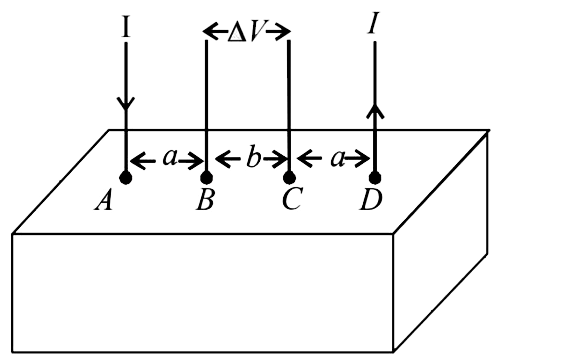
Delta V measured between B and C isView SolutionPassage-II:
Consider a block conducting material of resistivity .ρ. shown in the figure. Current .I. enters at .A. and leaves from .D.. We apply superposition principle to find voltage .ΔV. developed between .B. and .C.. The calculation is done in the following steps :
i) Take current .I. entering from .A. and assume it to spread over a hemispherical surface in the block.
ii) Calculate field E(r ) at distance .r. from A by using Ohm.s law E=ρj, where j is the current per unit area at .r..
iii) From the .r. dependence of E(r ), obtain the potential V(r ) at r.
iv) Repeat (i), (ii), (iii) for current .I. leaving .D. and superpose results for .A. and .D..
For current entering at A the electric field at a distance .r. from A isView Solution

