Consider situation in figure. The bottom of the pot is reflecting plane mimor, Fis a small fish and is an object. Refractive index of water is μ. Find the distances from it self the fish can see the image (s) of the object O.
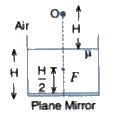
H(μ+1/2) above it self H,(μ+3/2) below it self
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-I)57videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions4videos
PRACTICAL PHYSICS
- BOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE - III3videos
SEMICONDUCTOR DEVICES
Similar Questions
Consider the situation in Fig. The bottom of the pot is a reflecting plane mirror, S is a small fish, and T is a human eye. Refractive index of water is μ.
a. At what distance(s) from itself will the fish see the image(s) of the eye?
b. At what distance(s) from itself will the eye see the image(s) of the fish?
 View Solution
View SolutionThe figure shows two plane mirrors parallel to each other and an object O placed between them. Then , the distances of the first three images from the mirror M2 will be (in cm)
View SolutionA tank contains a transparent liquid of refractive index μ. The bottom of the tank is a plane mirror as shown. A person at P looks at an object O and its image in the mirror. The distance between the object and its image in the mirror as preceived by the person is
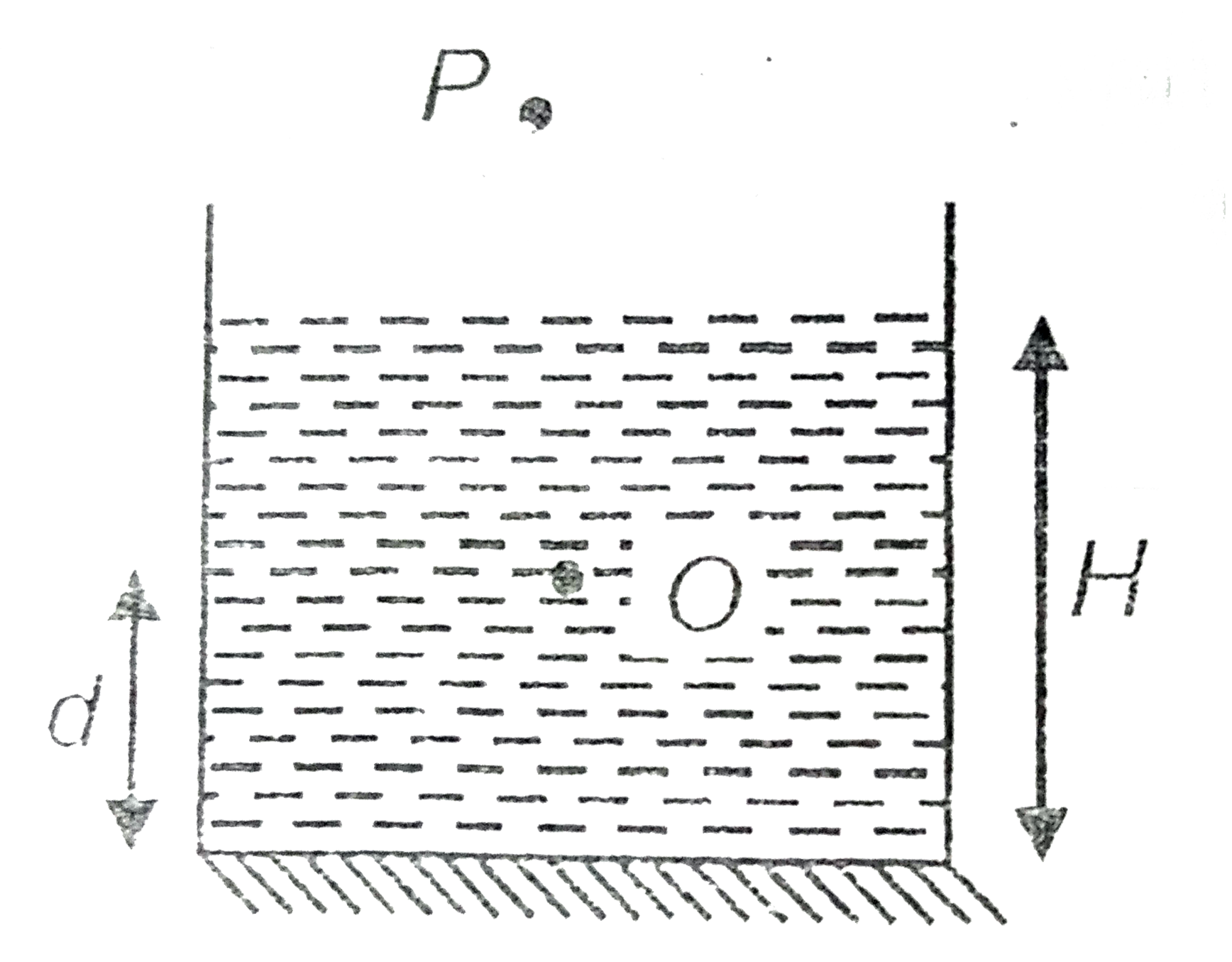 View Solution
View SolutionIn figure, a point source S is placed at a height h above the plane mirror in a medium of refractive index μ.
a. Find the number of images seen for normal view.
b. Find the distance between the images.
 View Solution
View SolutionAn object is placed at 24 cm distant from a surface of a lake. If water has refractive index of 4/3, then at what distance from the lake surface, a fish will get sight of an object.
View SolutionA thin equiconvex lens of refractive index 3/2 is placed on a horizontal plane mirror as shown in figure. The space between the lens and the mirror is filled with a liquid of refractive index 4/3 . It is found that when a point object is placed 15 cm above the lens on its priincipal axis, the object coincides with its own image.

Q. If another liquid is filled instead of water, the object and the image coincide at a distance 25 cm from the lens.
Calculate the refractive index of the liquid.View SolutionConsider the situation shown in figure. A plane mirror is fixed at a height h above the bottom of a beaker containing water (refractive index μ) up of a bottom formed by the mirror.Find the position of the image of bottom formed by the mirror.
 View Solution
View SolutionAn object O is kept in air and a lens of focal length 10cm (in air) is kept at the botton of a container which is filled upto a height 44cm by water. The refractive index of water is 4/3 and that of glass is 3/2. The botton of the container is closed by a thin glass slab of refractive index 3/2. Find the distance (in cm) of the final image formed by the system from botton of container (refer to figure shown below).
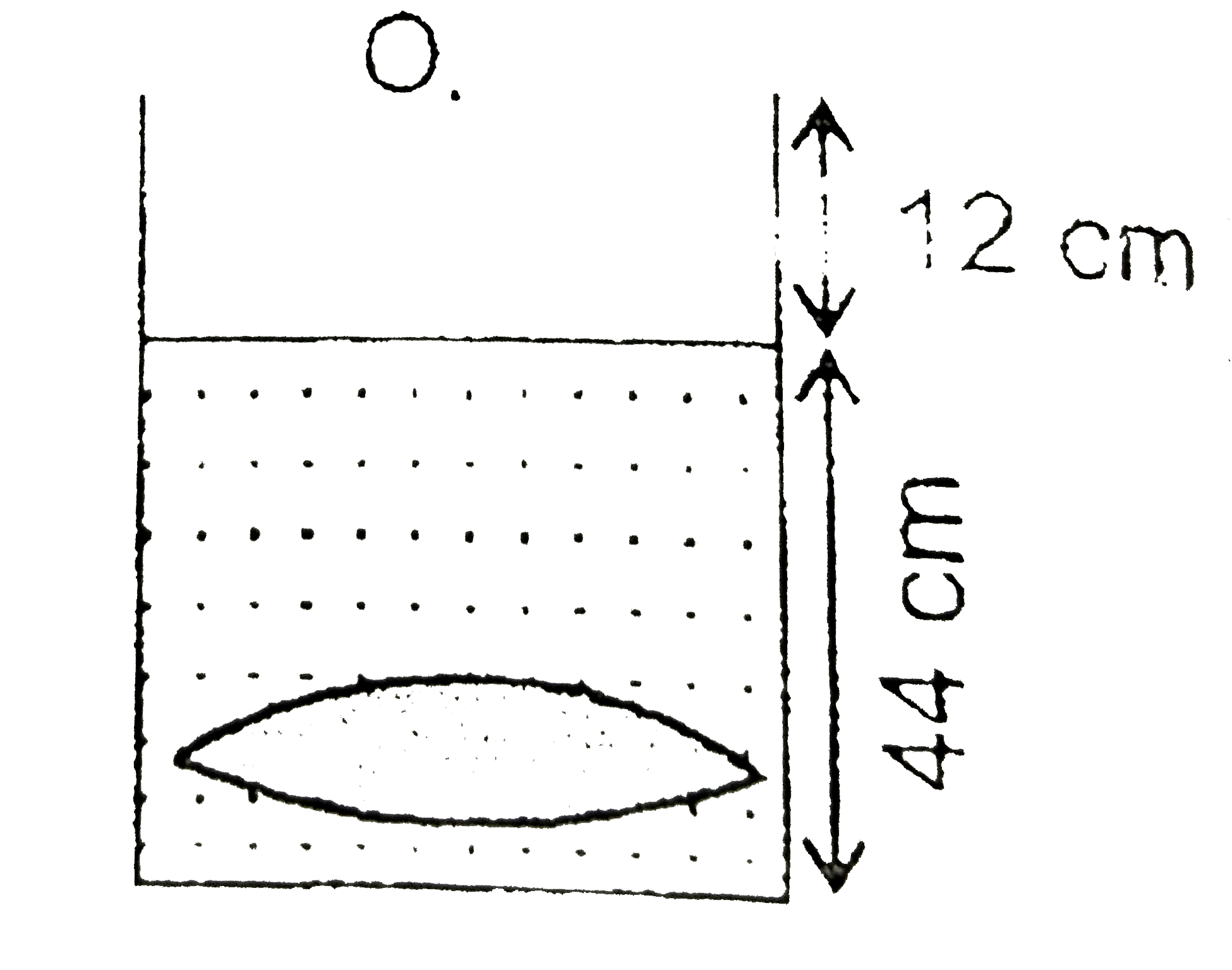 View Solution
View SolutionA beaker is filled with water as shown in figure (a). The bottom surface of the beaker is a concave mirror of large radius of curvature and small aperture. The height of water is h=40cm. It is found that when an object is placed 4 cm above the water surface, the image coincides with the object. Now the water level h is reduced to zero but there will still be some water left in the concave part of the mirror as shown in figure (b). The new height of the object h' above the new water surface so that the image again coincides with the object, will be (Refractive index of water =4/3)
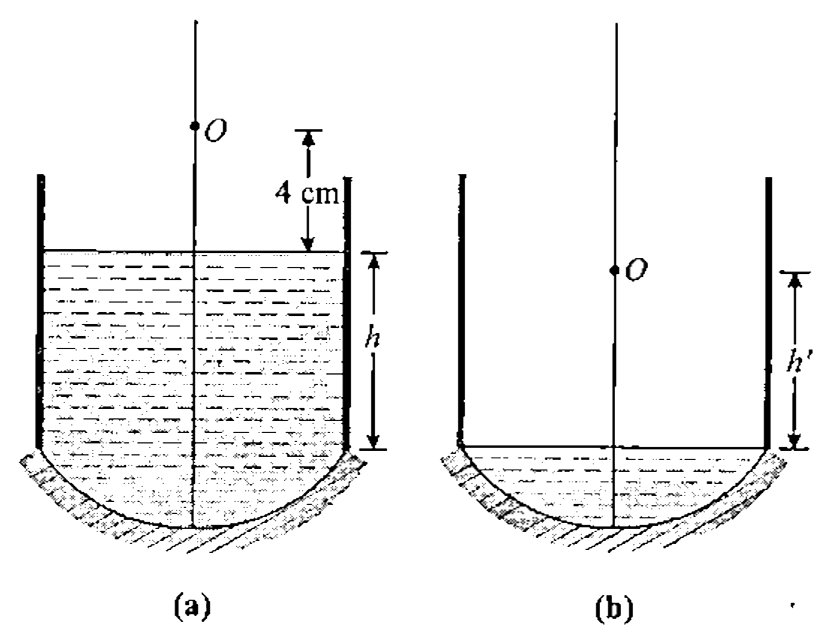 View Solution
View SolutionIf final image after two refractions through the lens and one reflection from the mirror forms at the same point O. Refrative index of the material of the lens μ=3/2. Then find d.
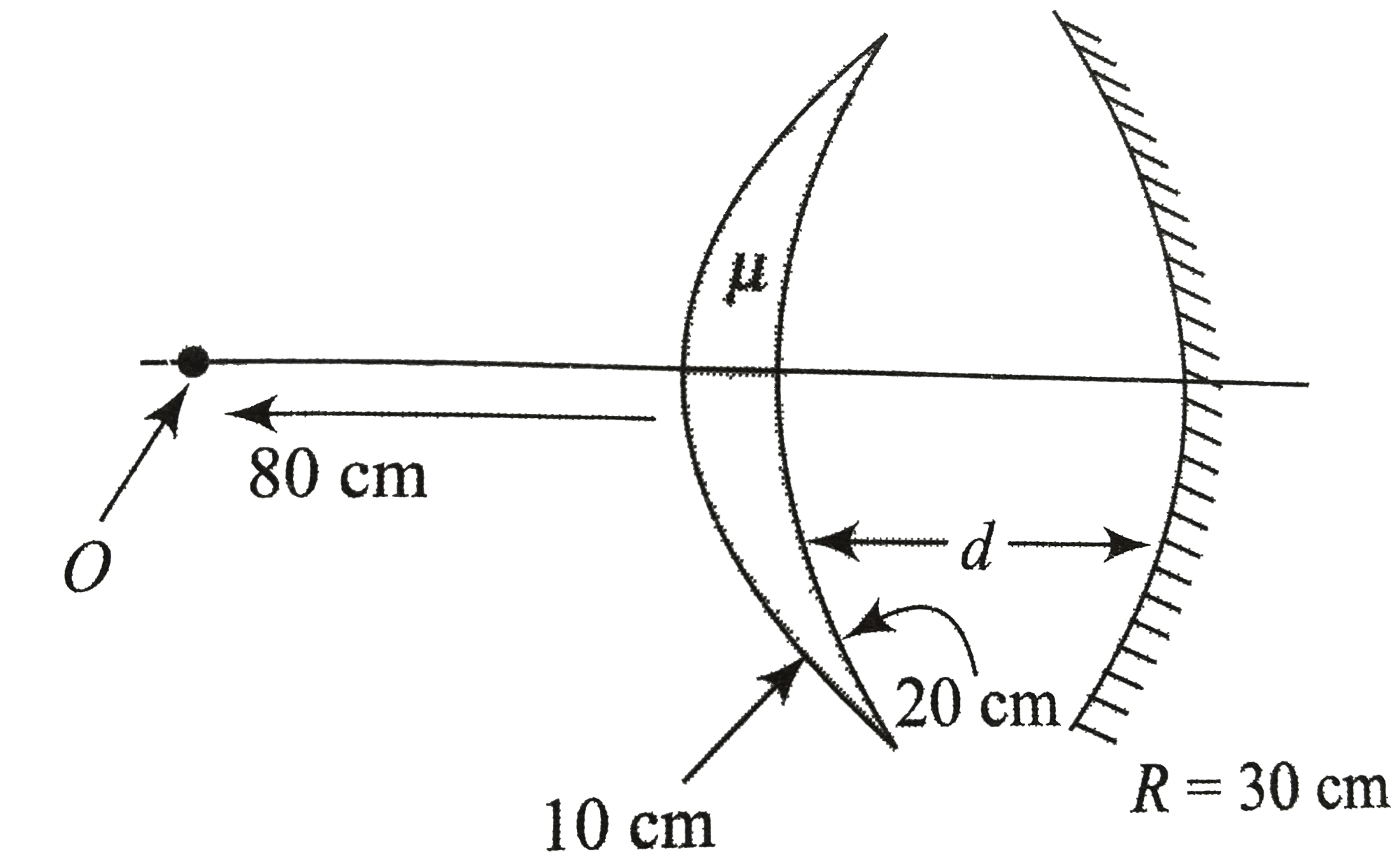 View Solution
View Solution

