Consider the following conclusiond regarding the components of an electric field at a certain point in space given by Ex=−Ky,Ey=Kx,Ez=0 .
The field is conservative.
The field is nonconservative.
The lines of force are straight lines.
The lines of force are circles.
The correct Answer is:B, D
b.,d.
Let us find potential difference between any two points:
V2−V1=−x2∫x1Exdx−y2∫y1Eydy
⇒V1−V1=+x2∫x1Kydx−y2∫y1Kxdy
This can further be evaluated only if we know the dependance of x and y on each other or the path of intergration. Hence field is nonconservative. To find the shape of lines of force:
tanθ=EyEx or dydx=EyEx
or dydx=Kx−Ky or xds+ydy=0
or x22+Y22=C or x2+y2=2C
This is the equation of circle.

Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type
94 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - CENGAGE PHYSICSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Question Bank
4 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
Figure shows electric lines of force. If Ex and Ey are the magnitudes of electric field at points x and y respectively, then
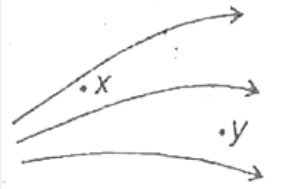
View SolutionIn the following question a statement of assertion (A) is followed by a statement of reason (R )
A: If E be electric field at a point , in free space then energy density at that point will be 12ε0E2 .
R , electrostatic field is a conservative field .
View Solution
Knowledge Check
Let V be the electric potential at a given point. Then the electric field Ex along x-direction at that point is given by :
A∫∞0VdxBdVdxC−dVdxD−VdVdxLet V be the electric potential at a given point. Then the electric field Ex along x-direction at that point is given by :
A∫∞0VdxBdVdxC−dVdxD−VdVdxIn the following question a statement of assertion (A) is followed by a statement of reason (R )
A: If E be electric field at a point , in free space then energy density at that point will be 12ε0E2 .
R , electrostatic field is a conservative field .AIf both Assertion & Reason are true and the reason is the correct explanation of the assertion , then mark (1).BIf both Assertion & Reason are true but the reason is not correct explanation of the assertion then mark (2)CIf Assertion is true statement but Reason is false, then mark (3)DIf both Assertion and Reason are false statements , then mark (4).
A graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y−andz−compo≠nts of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
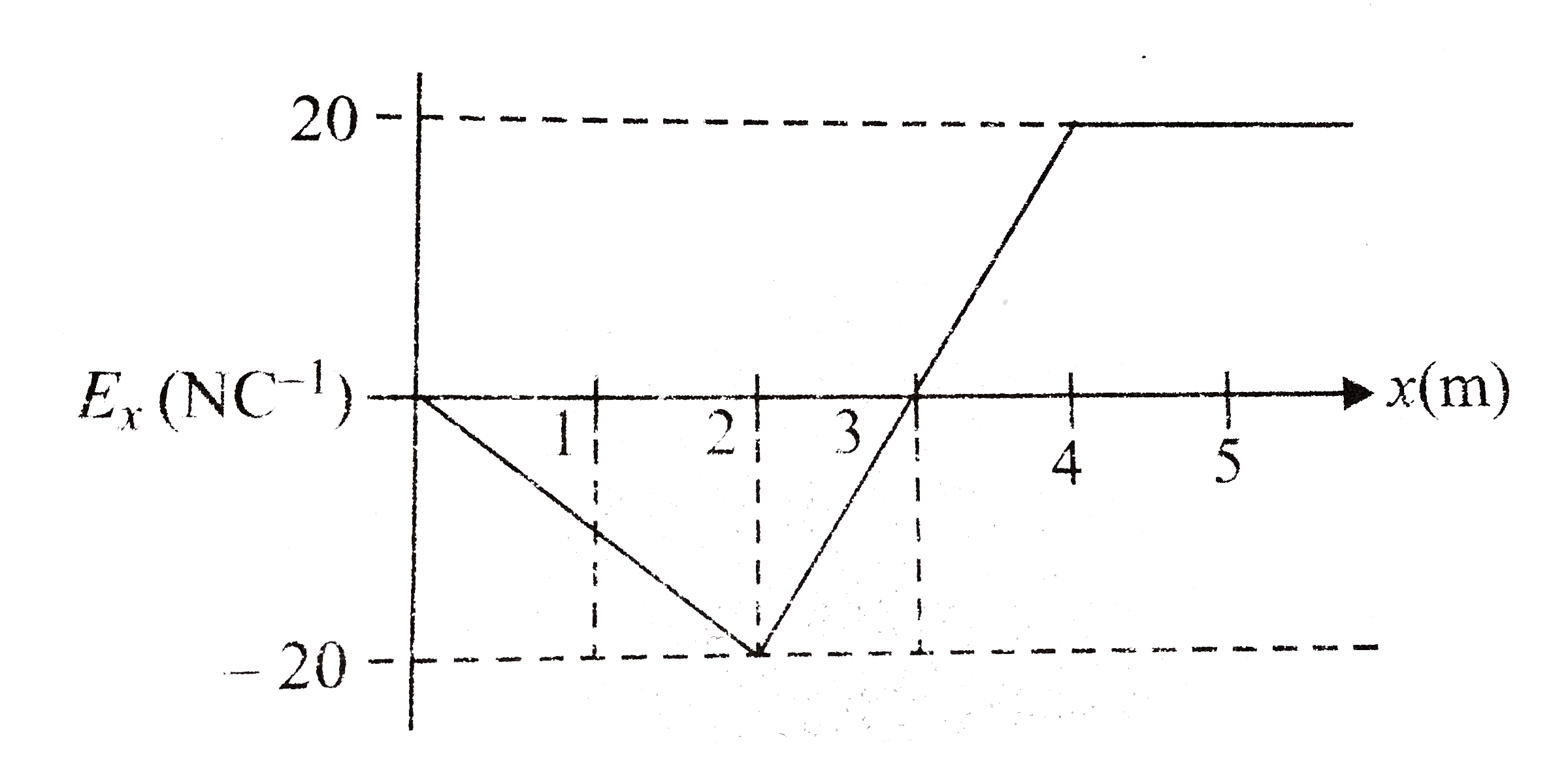
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y−andz−compo≠nts of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is

View SolutionA plane e.m. wave of frequency 30 MHz travels in free space along the x - direction. The electric field component of the wave at a particular point of space and time is E=6Vm−1 along y - direction. Its magnetic field component B at this point would be
View SolutionAn electromagnetic wave is propagating in vacuum along z-axis, the electric field component is given by Ex=E0sin(kz−ωt), then magnetic component is
View SolutionLet V0 be the potential at the origin in an electric field →E=Exˆi+Eyˆj. The potential at the point (x,y) is
View Solution
