Question

Consider the neutron capture reaction
${}^{109}Ag+n\to {}^{110}A>o{}^{110}Ag+\gamma$ (40-34)
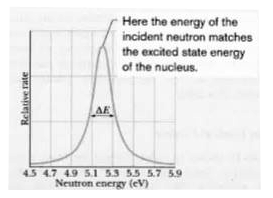
in which a compound nucleus $\left({}^{110}Ag\right)$ is formed. Figure 40-18 shows the relative rate at which such events take place, plotted against the energy of the incoming neutron. Find the mean lifetime of this compound nucleus by using the uncertainty principle in the form
$\Delta E.\Delta t\approx \hat{h}$. (40-35)
here $\Delta E$ is a mesure of the uncertainty with which the energy of a state can be defined. The quantity $\Delta t$ is a measure of the time available of measure this energy. In fact here $\Delta t$ is just $t_{\text{avg}}$, the average life of the compound nucleus befoe it decays to its ground state.
Reasoning: We see that the relative reaction rate peaks sharply at a neutron energy of about 5.2 eV.This suggests that we are dealing with a single excited energy level of the compund nucleus ${}^{110}Ag$. When the availabel energy(of the incoming neutron) just matches the energy of this level above the neutron) just matches the energy of this level above the ${}^{110}Ag$ ground state, we have resonance and the reaction of Eq. 40 -34 really goes.
However, the resonance peak is not infinitely sharp but has an approximate half peak is not infinitely shart but has an approximate half width ($\Delta E$ in the figue) of about 0.20 eV. We can account for this resonance peak width by saying that the excited level is not sharply defined in energy but has an energy uncertainty $\Delta E$ of about 0.20 eV.
Calculation : Subsitiuting that uncertainty of 0.20 2V into Eq. given us
$\Delta =t_{avg}\approx \frac{h}{\Delta E}\approx \frac{(4.14\times {10}^{-15}eV.s)/2\pi }{0.20eV}$
$\approx 3\times {10}^{-15}s$.
This is several hundraed times greater than the time a 5.2 eV neutron takes to cross the diameter of a ${}^{109}Ag$ nucleus . Therefore , the neutron is spending this time of $3\times {10}^{-15}$ s as part of the nucleus.

Explanation

Reasoning: We see that the relative reaction rate peaks sharply at a neutron energy of about 5.2 eV.This suggests that we are dealing with a single excited energy level of the compund nucleus `""^(110)Ag`. When the available energy(of the incoming neutron) just matches the energy of this level above the neutron) just matches the energy of this level above the `""^(110)Ag` ground state, we have resonance and the reaction of Eq. 40 -34 really goes.
However, the resonance peak is not infinitely sharp but has an approximate half peak is not infinitely shart but has an approximate half width (`DeltaE` in the figue) of about 0.20 eV. We can account for this resonance peak width by saying that the excited level is not sharply defined in energy but has an energy uncertainty `DeltaE` of about 0.20 eV.
Calculations: Substituting that uncertainty of 0.20 eV into Eq. 40-35 gives us
`Deltat=t_("avg")~~(hath)/(DeltAE)~~((4.14xx10^(15)eV.s)//2pi)/(0.20eV)`
`~~3xx10^(-15)s`
this is several hundred times greater than the time a 5.2 eV neutron takes to cross the diameter of a `""^(109)Ag` nucleus. Therefore, the neutron is spending this time of `3xx10^(-15)` as a part of the nucleus.