Consider the point P as the origin and time OP as the x-axis in the situation shown in the figure. Which of the following represents the coordinates of the image of the point object O. (Take OP=20cm)
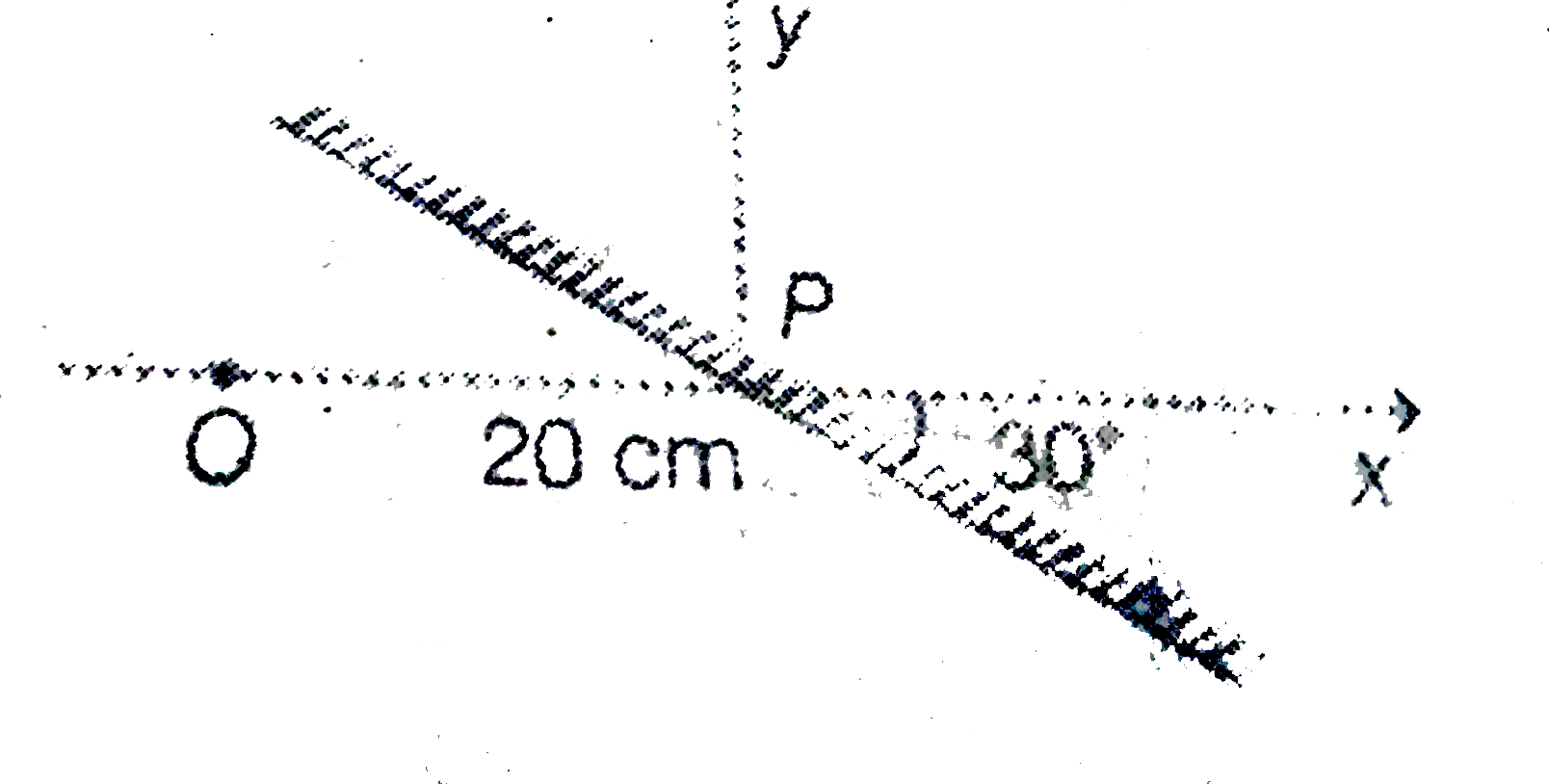
(20cm,0cm)
(10cm,10√3cm)
(−10cm,10√3cm)
(10cm,−10√3cm)
The correct Answer is:C
Step by step video, text & image solution for Consider the point P as the origin and time OP as the x-axis in the situation shown in the figure. Which of the following represents the coordinates of the image of the point object O. (Take OP = 20 cm) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - A. Only one option is correct (JEE Advance)
73 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct
20 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
Knowledge Check
A luminous point object is placed at O, whose image is formed at I as shown in the figure. AB is the optic axis. Which of the following statements are correct ?
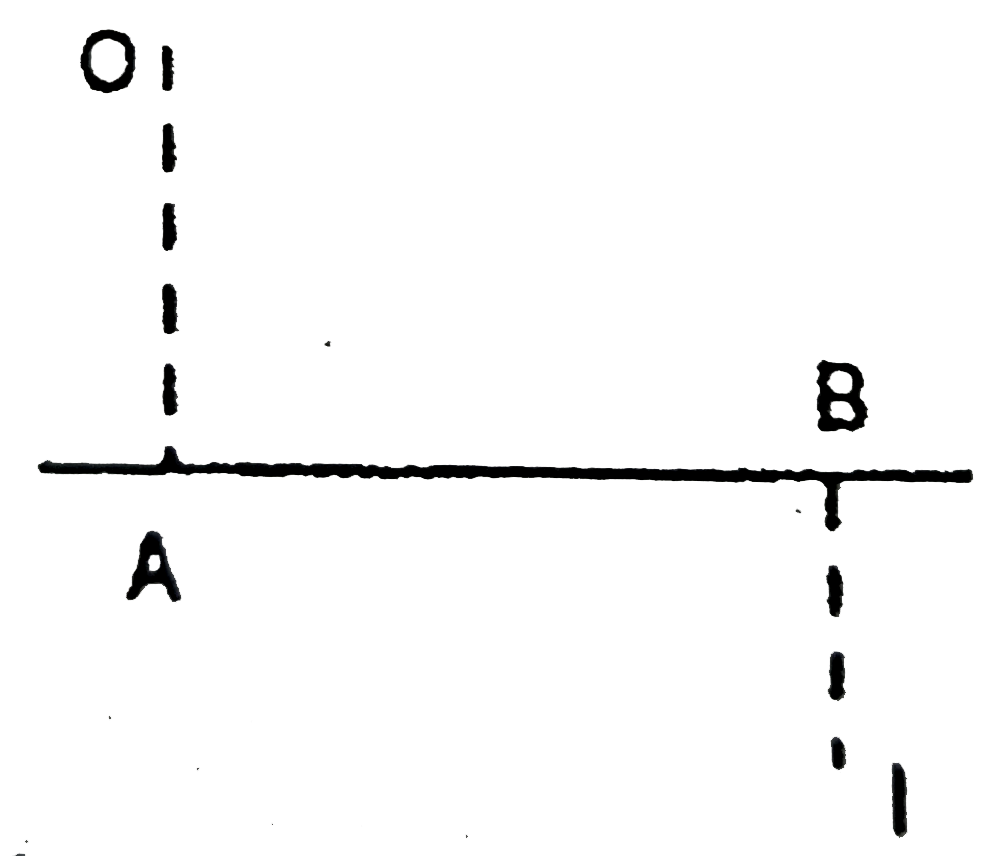 AIf a lens is used to obtain image, the lens must be converging.BIf a mirror is used to obtain image, the mirror must be a convex mirror having pole at the point of intersection of lines OI and AB.CPosition of principal focus of mirror cannot be found.DI is real image.
AIf a lens is used to obtain image, the lens must be converging.BIf a mirror is used to obtain image, the mirror must be a convex mirror having pole at the point of intersection of lines OI and AB.CPosition of principal focus of mirror cannot be found.DI is real image.If a line OP of length r (where, O is the origin) makes an angle α with X-axis and lies in the XZ-plane , then what are the coordinates of P?
A(rcosα,0,rsinα)B(0,0,rsinα)C(rcosα,0,0)D(0,0,rcosα)Let O be the origin and P be the point at a distance 3 units from origin. If direction ratios of OP are (1,-2,-2), then coordinates of P is given by
A(1,-2,-2)B(3,-6,-6)C(1/3,−2/3,−2/3)D(1/9,−2/9,−2/9)
If O is the origin, OP=3 with direction ratios −1,2,and−2, then find the coordinates of P.
View SolutionIn the figure,
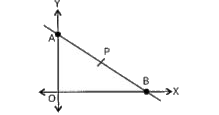
If P is the point (-cosθ,sinθ), then find the length of OP, where O is the origin.
View SolutionTwo large plane mirrors OM and ON are arranged at 150° as shown in the figure. P is a point object and SS' is a long line perpendicular to the line OP. Find the length of the part of the line SS' on which two images of the point object P can be seen.

View SolutionLet O be the origin and P be the point at a distance 3 units from origin. If direction ratios of OP are (1,−2,−2), then coordinates of P is given by
View SolutionConsider the rays shown in figure, as paraxial. The image of the virtual point object O formed by the lens LL is

View Solution
