Consider two heavy right circular rollers of the radii R and r respectively and rest on a rough horizontal plane a shown in figure. The larger roller has a string wound around it to which a horizontal force P can be applied as shown. Assuming that the coefficient of friction m has the same value for all surfaces of contact, determine the necessary condition under which the larger roller can be pulled over the smaller one. Assume the smaller cylinder should neither roll nor slide.

Figure shows the forces acting on the smaller cylinder. N1 is reaction between the two cylinders and N2 the normal reaction between the smaller cylinder and the horizontal surface.

The conditions of equlibrium are
∑Fx=N1cosα−μN2=μN1cos(90−α)=0.....i
Taking torque about O2 centre of smaller sphere
∑τ=μN1r−μN2r=0
N1=N2..........ii
On substituting equatiuons ii in i, we obtain
μN1+μN1sinα=N1cosα
μ(1+sinα)=cosα............iii
From figure b. sinα=√R−rR+r,cosα=2√RrR+r
Now equation iii becomes: μ(1+R−rR+r)=2√RrR+r
μ=√rR
Hence the required condition is μ≥√rR
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.2
17 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
Knowledge Check
A cubical box of side L rests on a rough horizontal surface with coefficient of friction p. A horizontal force F is a applied on the block as shown in Fig. 15.4.6. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
 AinfinitesimalBmg/4Cmg/2Dmg (−1μ)
AinfinitesimalBmg/4Cmg/2Dmg (−1μ)
A weight W rests on a rough horizontal plane,If the angle of friction is θ,the least force that can move the body along the plane will be
View SolutionA block of mass 20kg is placed on a rough horizontal plane and a horizontal force of 12N is applied. If coefficient of friction is 0.1 the frictional force acting on it is,
View Solution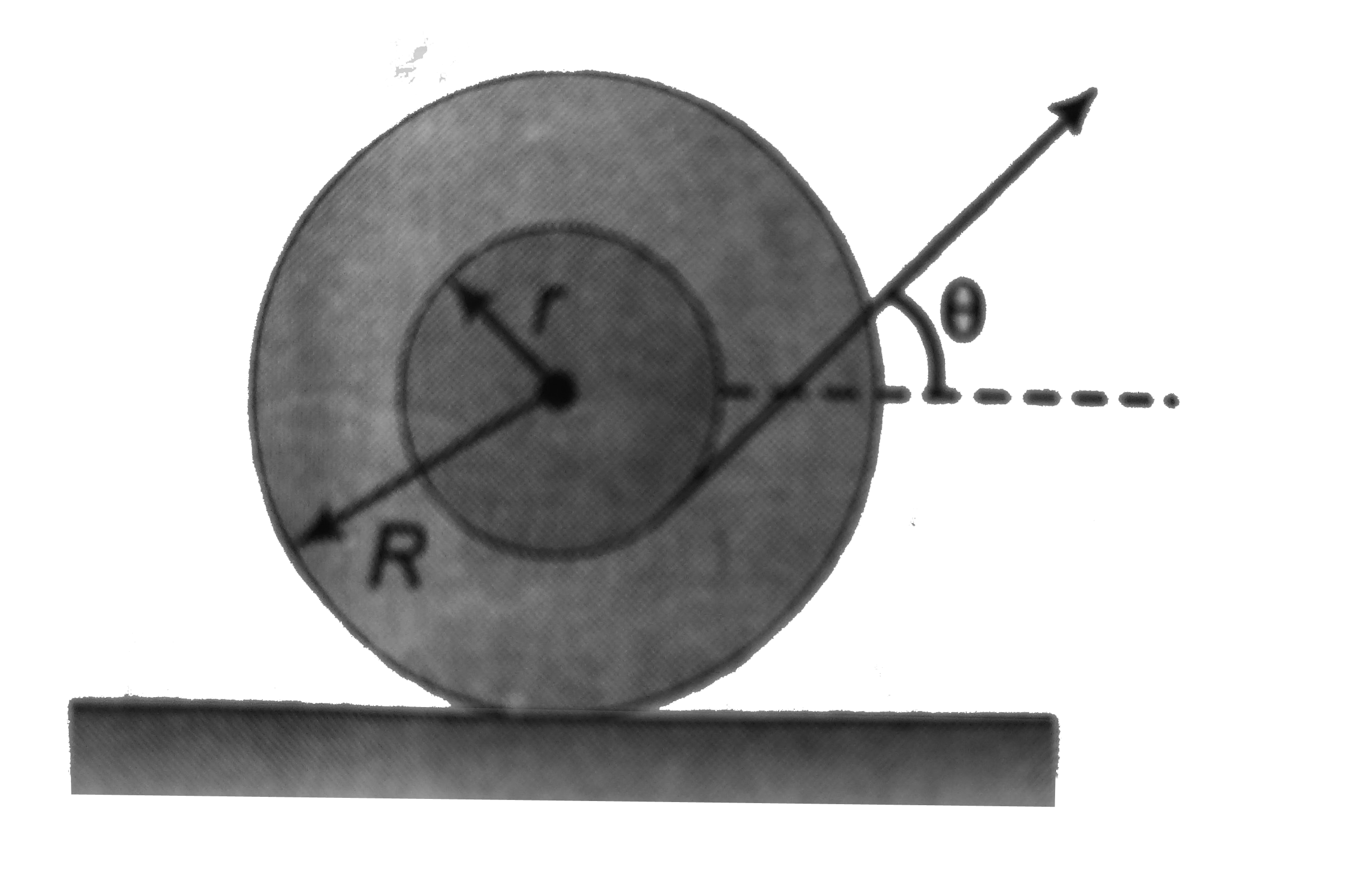
A spool is pulled at an angle θ with the horizontal on a rough horizontal surface as shown in the figure. If the spool remains at rest, the angle θ is equal to
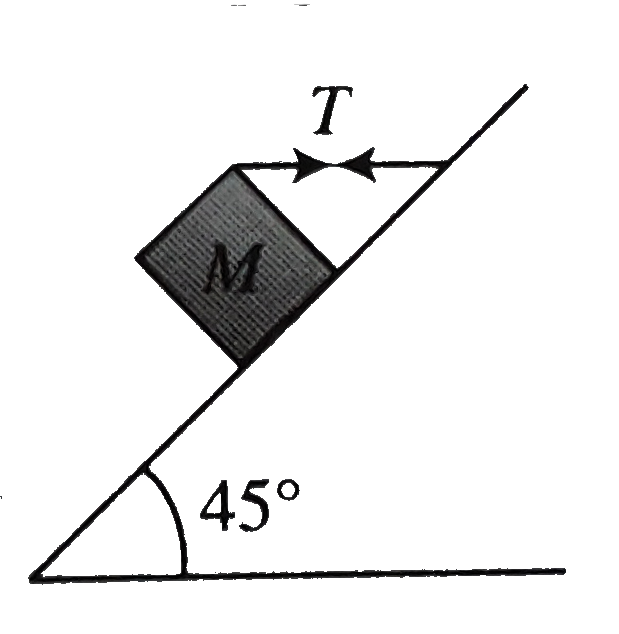
View SolutionA block of mass 15kg is resting on a rough inclined plane as shown in figure ,The block is tied by a horizontal string which has a tension 50N The coefficient of contact is
View SolutionTwo masses m1 and m2 are placed on a smooth horizontal surface and are connected by a string of negligible mass. A horizontal force F is applied on the mass m2 as shown in the figure. The tension in the string is

View SolutionTwo block A and B of masses 6kg and 3kg rest on a smooth horizontal surface as shown in figure If coefficient of friction between A and Bb is 0.4 the maximum horizontal force which can make them move without separation is

View SolutionTwo block A and B of masses 6kg and 3kg rest on a smooth horizontal surface as shown in figure If coefficient of friction between A and Bb is 0.4 the maximum horizontal force which can make them move without separation is

View Solution
