Consider two waves passing through the same string. Principle of superposition for displacement says that the net displacement of a particle on the string is sum of the displacements produced by the two waves individually. Suppose we state similar principles for the net velocity of the particle and the net kinetic energy of the particle. Such a principle willl be valid for
both the velocity and the kinetic energy
the velocity but not for the kinetic energy
the kinetic energy but not for the velocity
neither the velocity nor the kinetic energy.
The correct Answer is:B
Step by step video, text & image solution for Consider two waves passing through the same string. Principle of superposition for displacement says that the net displacement of a particle on the string is sum of the displacements produced by the two waves individually. Suppose we state similar principles for the net velocity of the particle and the net kinetic energy of the particle. Such a principle willl be valid for by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMACHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Objective 2
9 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMACHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Objective -2
1 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMACHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Short Answer
7 Videos
- THE FORCESBOOK - HC VERMACHAPTER - THE FORCESEXERCISE - Exercises
12 Videos
- WORK AND ENERGYBOOK - HC VERMACHAPTER - WORK AND ENERGYEXERCISE - Exercises
64 Videos
Similar Questions
A series of pulses, each of amplitude 0.150m, are sent on a string that is attached to a wall at one end. The pulses are reflected at the wall and travel back along the string without loss of amplitude. When two waves are present on the same string. The net displacement of a given point is the sum of the displacement of the individuals waves at the point. What is the net displacement at point on the spring where two pulses am crossing, (a) if the string is rigidly attached to the post? (b) if the end at which reflection occurs is free is slide up and down ?
View SolutionFind the net displacement of a particle from its starting point if it undergoes two sucessive displacement given by →S1=20m,37∘ North of West , →S2=50m,53∘ North of East.
View Solution
Knowledge Check
A transverse wave passes through a medium, the maximum speed of the vibrating particle when the displacement of the particle from the mean position is
AzeroBequal to the amplitudeChalf of the amplitudeDmidway between mean and extreme positionFor a sine wave passing through a medium, let y be the displacement of a particle, v be its velocity and a be its acceleration :-
Ay,v and a are always in the same phaseBy and a are always in opposite phaseCPhase difference between y and v is π2DPhase difference between v and a is π2Assertion: Standing waves are formed when amplitudes of two constituent waves are equal.
Reason: At any point net displacement at a given time is resultant of displacement of constituent waves.AIf both Assertion and Reason are true and the Reason is correct explanation of the Assertion.BIf both Assertion and Reason are true but Reason is not the correct explanation of Assertion.CIf Assertion is true, but the Reason is false.DIf Assertion is false but the Reason is true.
When a sound wave of frequency 300 Hz passes through a medium the maximum displacement of a particle of the medium is 0.1 cm . The maximum velocity of the particle is equal to
View SolutionFigure (i) and (i) show the displacement-time graphs of two particles moving along the x-axis. We can say that
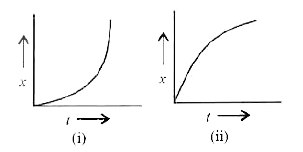
View SolutionThe displacement of a particle of a string carrying a travelling wave is given by y = (3 cm) sin 6.28 (0.50 x – 50 t) where x is in centimeter and t is in second. The velocity of the wave is-
View SolutionThe displacement y (in cm ) produced by a simple harmonic wave is
y=10πsin(2000πt−πx17) . The periodic time and maximum velocity of the particles in the medium will respectively be
View SolutionStatement-1: Two particles acted by same net force for same time always have same kinetic energy
Statement-2: Two particles acted by same net force having same displacement always have same kinetic energy.
View Solution
