Cosmic rays are charged particles that strike out atmosphere from some external source. We find that more low-energy cosmic rays reach the earth at the north and south magnetic poles than at the (magnetic) equator. Why it is so?
The earth.s magnetic field is vertical at the poles, which implies that it is parallel to the velocity of the charged particles in cosmic rays. So, no force will act on the charged particles. At the equator, however, the earth.s magnetic field is horizontal, which implies that it is perpendicular to the velocity of the charged particles. Maximum force will act on the charged particles in this case. For this reason, the low energy particles are deflected sideways and only the high-energy particles are able to reach equator.
Topper's Solved these Questions
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - TOUGH AND TRICKY PROBLEM
5 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - NCERT FILE (NCERT TEXTBOOK EXERCISE)
26 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - PRACTICE PROBLEM
28 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Chapter Practice Test
9 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - CHAPTER PRACTICE TEST
13 Videos
Similar Questions
A bar magnet of magnetic moment 2.0Am2 is free to rotate about a vertical axis through its centre. The magnet is released from rest from the east-west position. Find the kinetic energy of the magnet as it takes the north-south position. The horizontal component of the earth's magnetic field is B=25μT.
View SolutionA bar of magnetic moment 2.5Am2 is free to rotate about a vertical axis through its centre . The magnet is released from the rest from the east - west direction . Find the kinetic energy of the magnet as it aligns itself in the north - south direction . The horizontal component of earth's magnetic field is 0.3G
View Solution
Knowledge Check
Due to the earth's magnetic field, charged cosmic ray particles
ACan nevar reach the poleBCan never reach the equatorCRequired greeter kinetic energy to reach the equalor than poleDRequir less kinetic energy to reach the equator than poleA bar magnet of magnetic moment 2.0 A−m2 is free to rotate about a vertical axis through its centre. The magnet is released from rest from the east west position. Find the kinetic energy of the magnet as it takes the north south position. The horizontal component of the earth's magnetic field as B=25μT. Earth's magnetic field is from south to north.
A40μJB50μJC60μJD70μJThe fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.
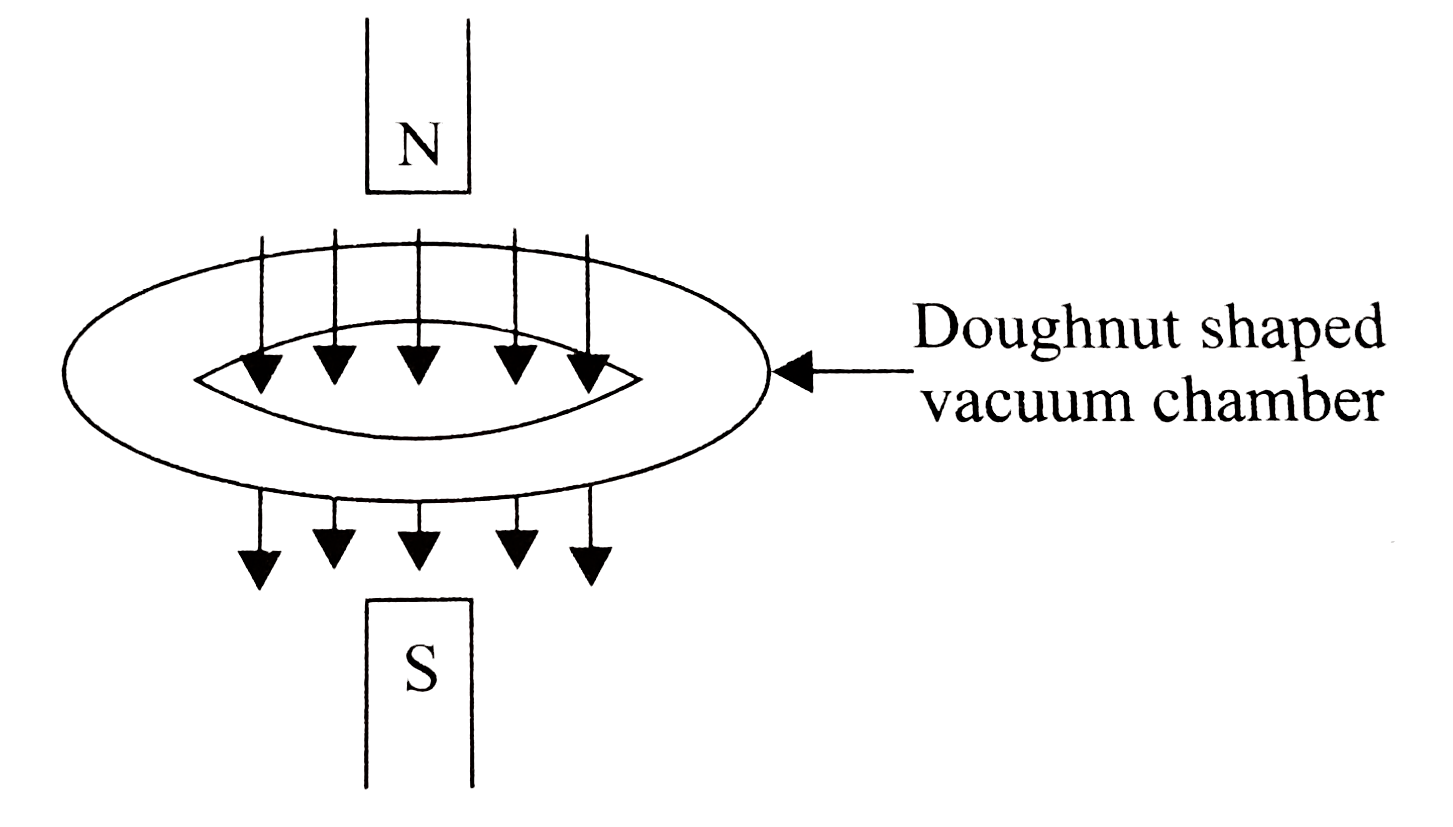
An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Variable magnetic fluxAcan chane sinusoidallyBshould either increase or decrease all the timeCmust becomes zero when induced field is maximumDnone of these
One charged particle with +2e charge is projected from west to east with a speed of 2×106 m/s. A magnetic field of 2 T exists in the direction south to north. Find the magnetic force acting on the charged particle. In which direction the particle is going to get deviated? Neglect gravity and other forces.
View SolutionThe fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.
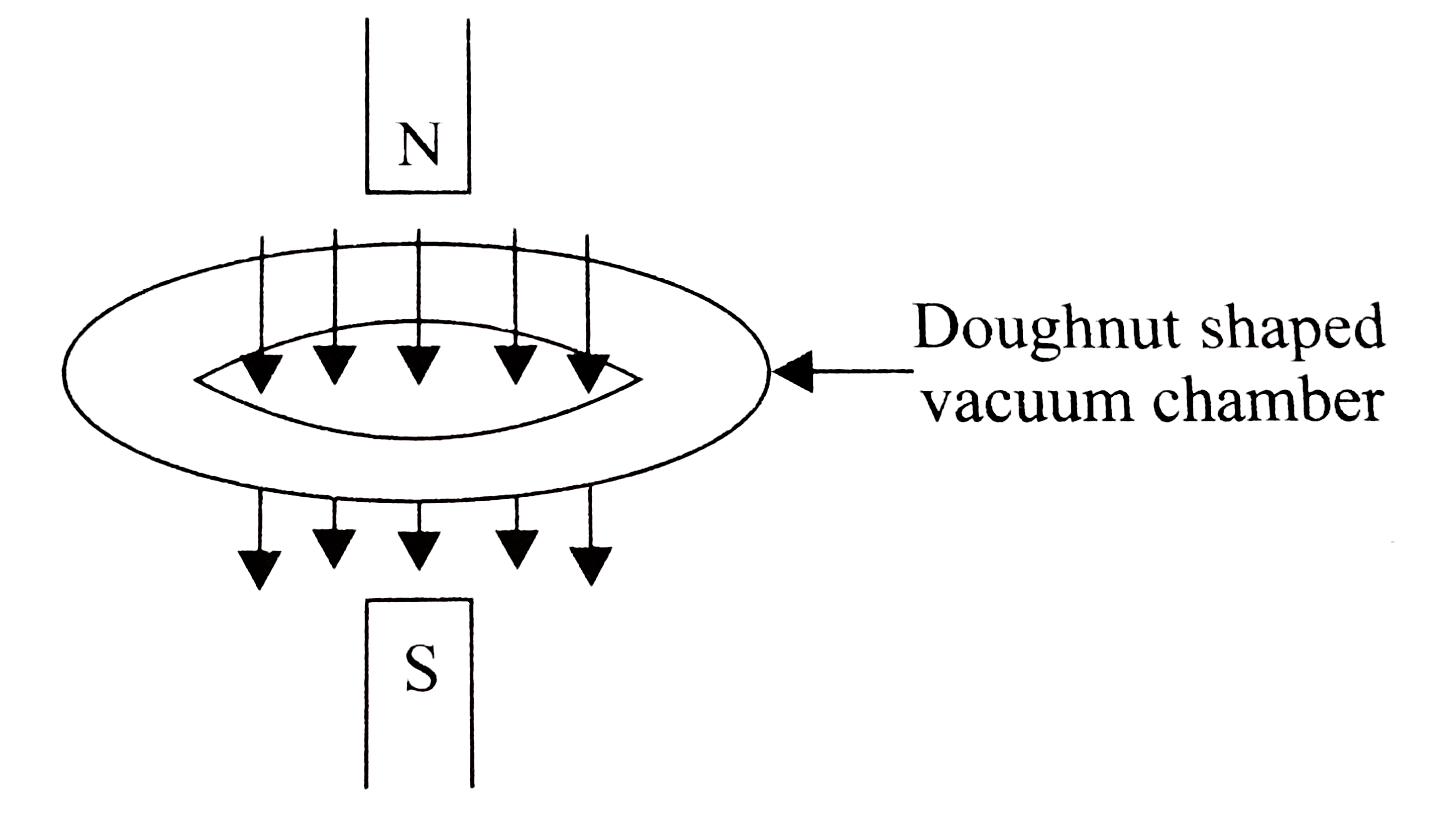
An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Magnetic field which keeps the particles in circular path must
View SolutionThe fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.
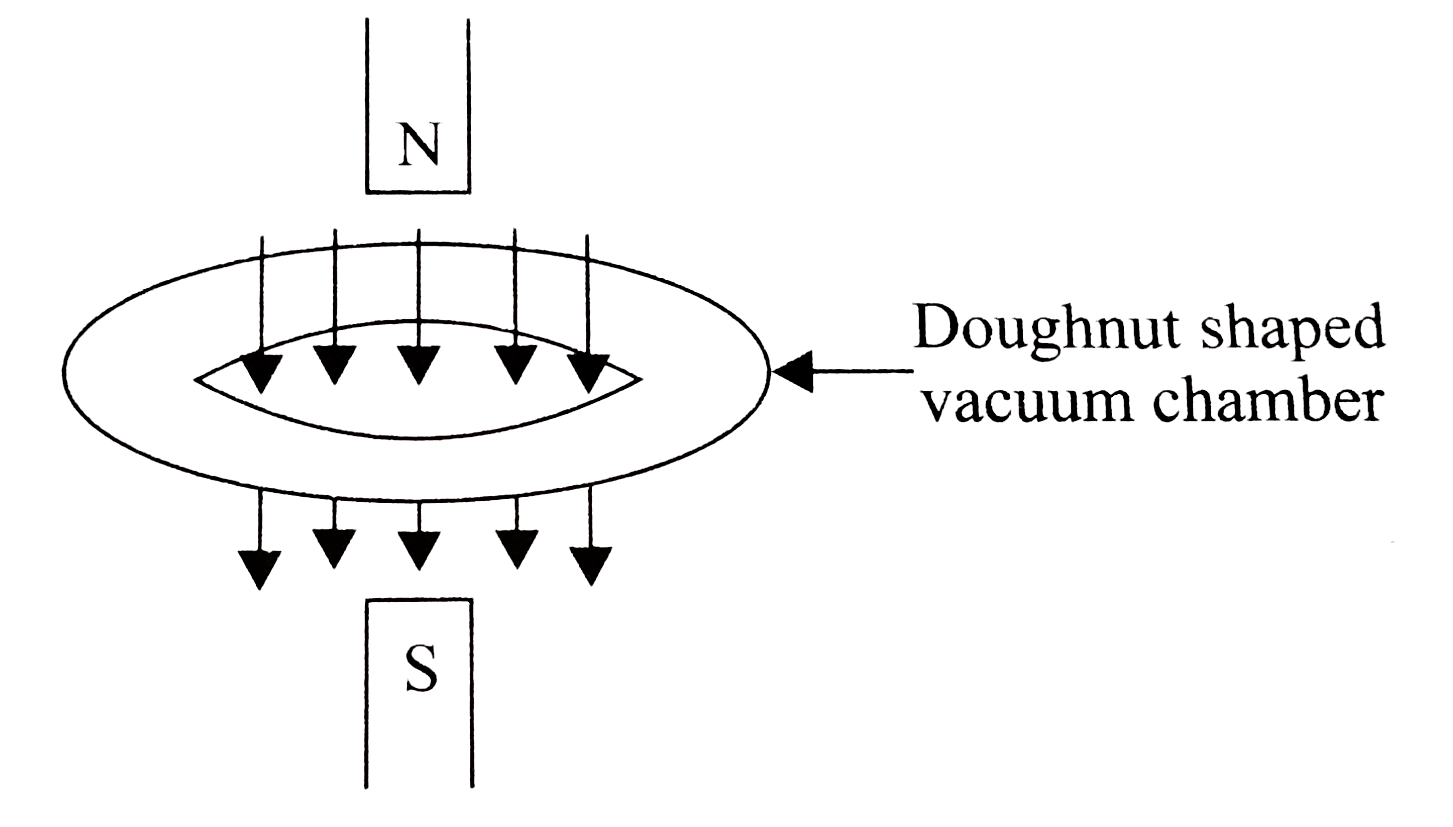
An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Working of betatron is not based upon which of the following theories?
View SolutionRead the following text and answer the following questions on the basis of the same:
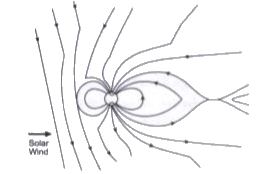
If we move into space and study the Earth's invisible magnetic field, it wouldn't really look like a bar magnet at all. Earth's magnetic field gets stretched out into a comet-like shape with a tail of magnetism that stretches millions of miles behind the earth, opposite to the Sun. The Sun has a wind of gas that pushes the earths field from the left to the right in the picture.
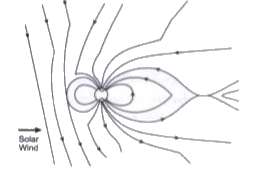
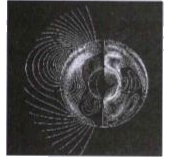
The core of the Earth is an electromagnet. Although the crust is solid, the core of the Earth is surrounded by a mixture of molten iron and nickle. The magnetic field of Earth is caused by currents of electricity that flow in the molten core. These currents are hundreds of miles wide and flow at thousands of miles per hour as the Earth rotates. The powerful magnetic field passes out through the core of the Earth, passes through the crust and enters space. This picture shows the solid inner core region (inner circle) surrounded by a molten outer core (the area between the two circles). The currents flow in the outer core, travel outwards through the rest of the earth's interior. If the Earth rotated faster, it would have a stronger magnetic field.
By the time the field has reached the surface of Earth, it has weakened a lot, but it is still strong enough to keep your compass needles pointed towards one of its poles. All magnets have two poles: a North Pole and a South Pole. The magnetic poles of earth are not fixed on the surface, but wander quite a bit. The pole in the Northern Hemisphere seems to be moving northwards in geographic latitude by about 10 kilometres per year by an average.
The magnetic poles of Earth are:
View SolutionRead the following text and answer the following questions on the basis of the same:
If we move into space and study the Earth's invisible magnetic field, it wouldn't really look like a bar magnet at all. Earth's magnetic field gets stretched out into a comet-like shape with a tail of magnetism that stretches millions of miles behind the earth, opposite to the Sun. The Sun has a wind of gas that pushes the earths field from the left to the right in the picture.
The core of the Earth is an electromagnet. Although the crust is solid, the core of the Earth is surrounded by a mixture of molten iron and nickle. The magnetic field of Earth is caused by currents of electricity that flow in the molten core. These currents are hundreds of miles wide and flow at thousands of miles per hour as the Earth rotates. The powerful magnetic field passes out through the core of the Earth, passes through the crust and enters space. This picture shows the solid inner core region (inner circle) surrounded by a molten outer core (the area between the two circles). The currents flow in the outer core, travel outwards through the rest of the earth's interior. If the Earth rotated faster, it would have a stronger magnetic field.

By the time the field has reached the surface of Earth, it has weakened a lot, but it is still strong enough to keep your compass needles pointed towards one of its poles. All magnets have two poles: a North Pole and a South Pole. The magnetic poles of earth are not fixed on the surface, but wander quite a bit. The pole in the Northern Hemisphere seems to be moving northwards in geographic latitude by about 10 kilometres per year by an average.
Earth's magnetic field may increase if:
View Solution
