Current in a long current carrying wire is I=2t
A conducting loop is placed to the right of this wire. Find

a. magnetic flux ϕB passing through the loop.
b. induced emf|e| prodced in the loop.
c. if total resistance of the loop is R, then find induced current Iin in the loop.
Here no conductor is in motion. So we can apply only method -1. Further, magnetic field of straight wire is non uniform. Therefore, magnetic flux can be obtained by integration.
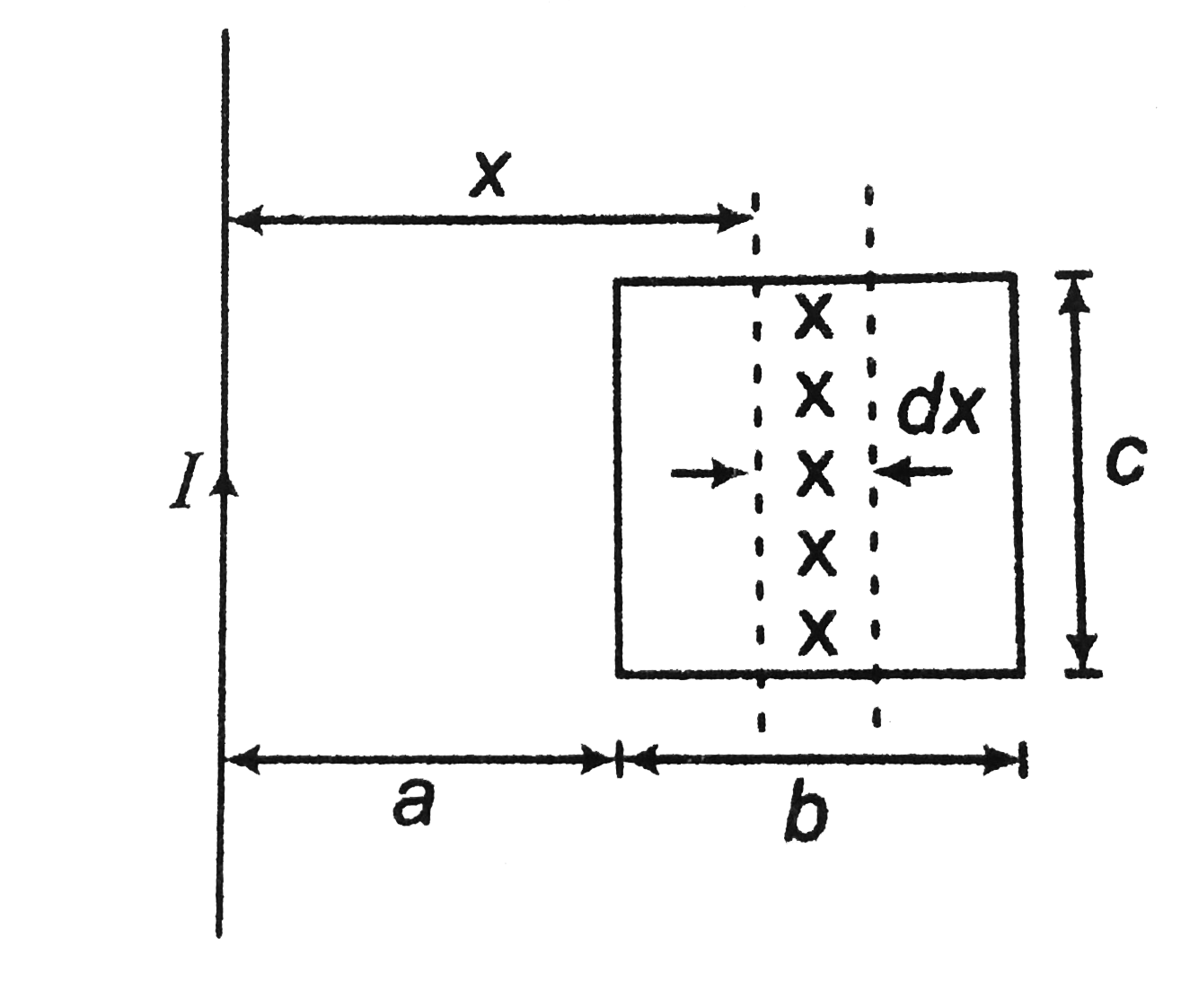
a. At a distance x from the staight wire magnetic field is
B=μ02πIx [in ⊗ direction]
Let us take a smal strip of width dx.
∴ Area of this strip is
dS=c(dx)
Now, dS can also be assumed inwards. or, angle between B and dS may be assumed to be 0∘
Therefore, small magnetic flux passing through the loop is
dϕB=BdScos0∘
μ02πIxcdx
Total magnetic flux is
ϕB=∫x=a+bx=adϕB
=∫a+ba(μ0IC2π)dxx
=μ0IC2πln(a+ba)
Substituting the value of I we get
ϕB=μ0ctπln(a+ba)
b. |e|=∣∣∣dϕBdt∣∣∣=ddt[μ0ctπln(a+ba)]
=μ0cπln(a+ba)
c. Induced current
Iin=|e|R=μ0CπRln(a+ba)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 2
2 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 3
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A constant current I flows through a long straight wire as shown in figure. A square loop starts moving towards righ with as constant speed v.

a Find induced emf produced i the loop as a function x
b. If total resistance of the loop is R, then find induced current in the loop,
View SolutionAn electron is moving near to a conducting loop then the induced current in the loop is-
View SolutionA circular loop is placed in magnetic field B=2t. Find the direction of induced current produced in the loop.

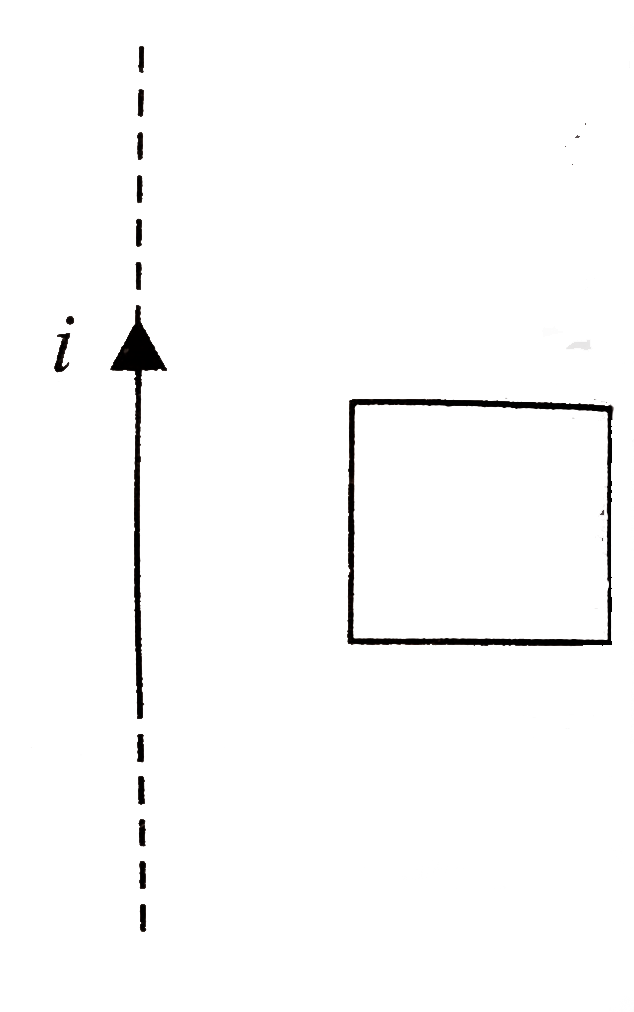
View SolutionA square conducting loop is placed in the neighbourhood of a coplaner long straight wire carrying a current i.
View SolutionShows a long current carrying wire and two rectangular loops moving with of velocity v. Find the direction of current in each loop.
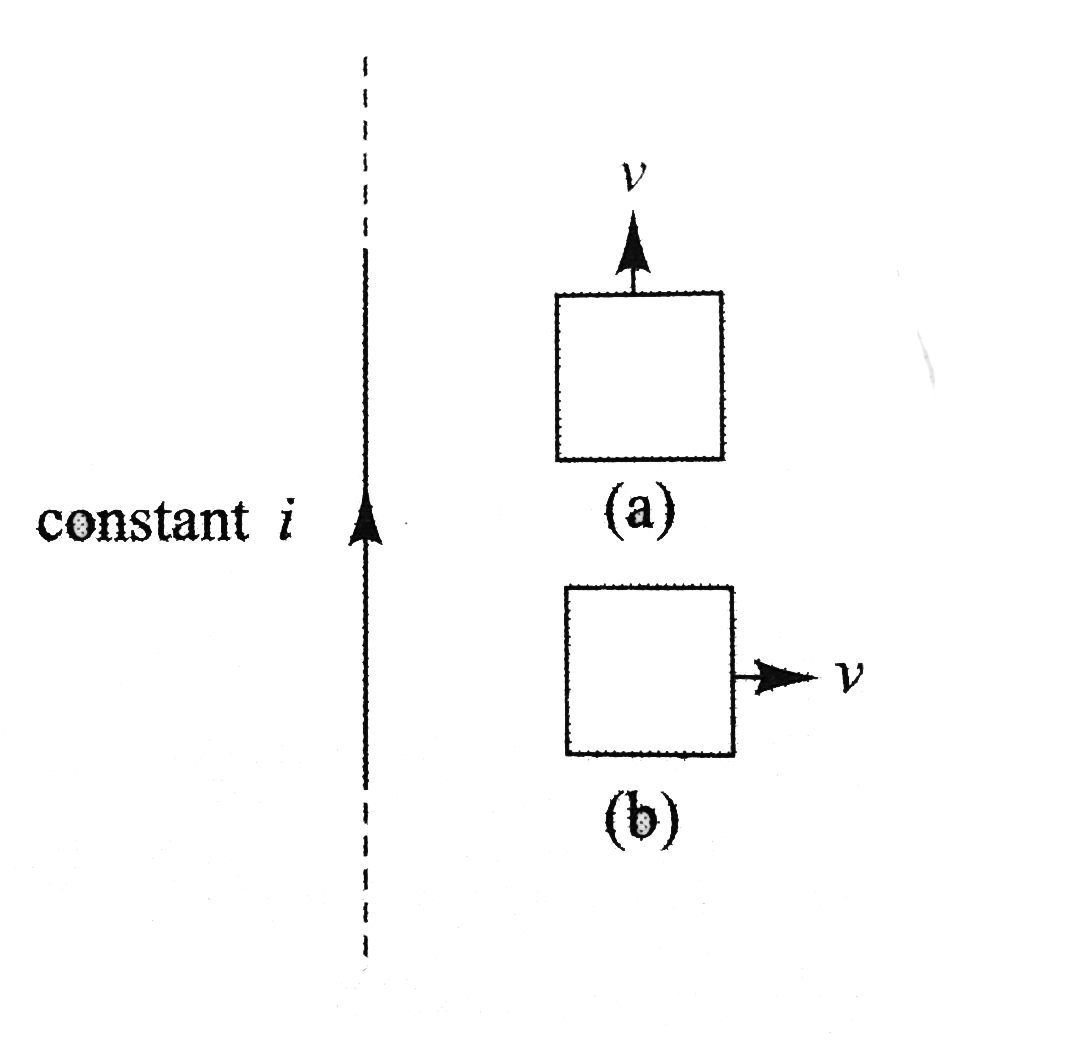
View SolutionShows a long current carrying wire and two rectangular loops moving with of velocity v. Find the direction of current in each loop.

View SolutionShows a long current carrying wire and two rectangular loops moving with of velocity v. Find the direction of current in each loop.

View SolutionA rectangular loop is placed near a current carrying straight wire as shown in the figure. If the loop is rotated about an axis passing throught one of its sides find the direction of induced current in the loop.
View SolutionA long wire carrying a steady current I lies in the plane of circular conducting loop placed at a certain distance from the wire. There will be an induced current in the loop if it is
View SolutionFigure shows a conducting loop placed near a long straight wire carrying a current i as shown, if the current increases continuously, find the direction of the induced current in the loop.

View Solution
