A potentiometer wire is 100cm long hand a constant potential difference is maintained across it. Two cells are connected in series first to support one another and then in opposite direction. The balance points are obatined at 50cm and 10cm from the positive end of the wire in the two cases. The ratio of emfs is:
5:4
3:4
3:2
5:1
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the Setup
We have a potentiometer wire of length 100cm with a constant potential difference across it. Two cells are connected in two different configurations: first in series supporting each other and then in opposite directions.
Step 2: Define the First Case
In the first case, when the cells are connected in series supporting each other, the total EMF E is given by:
E=E1+E2
The balance point is obtained at 50cm from the positive end of the wire. According to the potentiometer principle, the EMF is proportional to the length of the wire:
E∝L1(where L1=50cm)
Thus, we can write:
E1+E2∝50(Equation 1)
Step 3: Define the Second Case
In the second case, when the cells are connected in opposite directions, the total EMF E is given by:
E=E1−E2
The balance point is obtained at 10cm from the positive end of the wire:
E∝L2(where L2=10cm)
Thus, we can write:
E1−E2∝10(Equation 2)
Step 4: Set Up the Ratios
From Equations 1 and 2, we can express the relationships as:
E1+E2E1−E2=5010
This simplifies to:
E1+E2E1−E2=5
Step 5: Cross Multiply and Rearrange
Cross-multiplying gives:
E1+E2=5(E1−E2)
Expanding this, we have:
E1+E2=5E1−5E2
Rearranging terms leads to:
E1+E2+5E2=5E1
This simplifies to:
6E2=4E1
Step 6: Solve for the Ratio of EMFs
Dividing both sides by E2 and E1 gives:
E1E2=64=32
Conclusion
Thus, the ratio of the EMFs E1 and E2 is:
E1E2=32
We have a potentiometer wire of length 100cm with a constant potential difference across it. Two cells are connected in two different configurations: first in series supporting each other and then in opposite directions.
In the first case, when the cells are connected in series supporting each other, the total EMF E is given by:
E=E1+E2
The balance point is obtained at 50cm from the positive end of the wire. According to the potentiometer principle, the EMF is proportional to the length of the wire:
E∝L1(where L1=50cm)
Thus, we can write:
E1+E2∝50(Equation 1)
In the second case, when the cells are connected in opposite directions, the total EMF E is given by:
E=E1−E2
The balance point is obtained at 10cm from the positive end of the wire:
E∝L2(where L2=10cm)
Thus, we can write:
E1−E2∝10(Equation 2)
From Equations 1 and 2, we can express the relationships as:
E1+E2E1−E2=5010
This simplifies to:
E1+E2E1−E2=5
Cross-multiplying gives:
E1+E2=5(E1−E2)
Expanding this, we have:
E1+E2=5E1−5E2
Rearranging terms leads to:
E1+E2+5E2=5E1
This simplifies to:
6E2=4E1
Dividing both sides by E2 and E1 gives:
E1E2=64=32
Thus, the ratio of the EMFs E1 and E2 is:
E1E2=32
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
A potentiometer wire is 5 m long and a potential difference of 6V is maintained between its ends. Find the emf of a cell which balance against a length of 180 cm of the potentiometer wire.
View SolutionThere is a definite potential difference between the two ends of a potentiometer. Two cells are connected in such a way that first time help each other, and second time they oppose each other. They are balanced on the potentiometer wire at 120cm and 60cm length respectively. compare the electromotive force of the cells. potentiometer wire at 120cm and 60cm length respectively. Compare the electromotive force of the cells.
View Solution
Knowledge Check
A potentiometer wire of length 100 cm has a resistance of 100Ω it is connected in series with a resistance and a battery of emf 2 V and of negligible internal resistance. A source of emf 10 mV is balanced against a length of 40 cm of the potentiometer wire. what is the value of the external resistance?
A790ΩB890ΩC990ΩD1090Ω
The length of a wire of a potentiometer is 100 cm, and the e.m.f. of its standard cell is E volt. It is employed to measure the e.m.f. of a battery whose internal resistance is 0.5Ω. If the balance point is obtained at I = 30 cm from the positive end, the e.m.f. of the battery is .
where i is the current in the potentiometer wire.
View SolutionIn a metre bridge, the length of the wire is 100 cm. At what position will the balance point be obtained if the two resistances are in the ratio 2 : 3?
View SolutionTwo long parallel current carrying conductors 30 cm apart having current each of 10 A in opposite direction, then value of magentic field at a point of 10 cm between them, from any of the wire.
View SolutionIn the figure a long uniform potentiometer wire AB is having a constant potential gradient along its length. The null points for the two primary cells of emfs ε1 and ε2 connected in the manner shown are obtained at a distance of 120 cm and 300 cm from the end A. Find (i) ε1/ε2 and (ii) position of null point for the cell ε1.
How is the sensitivity of a potentiometer increased ?
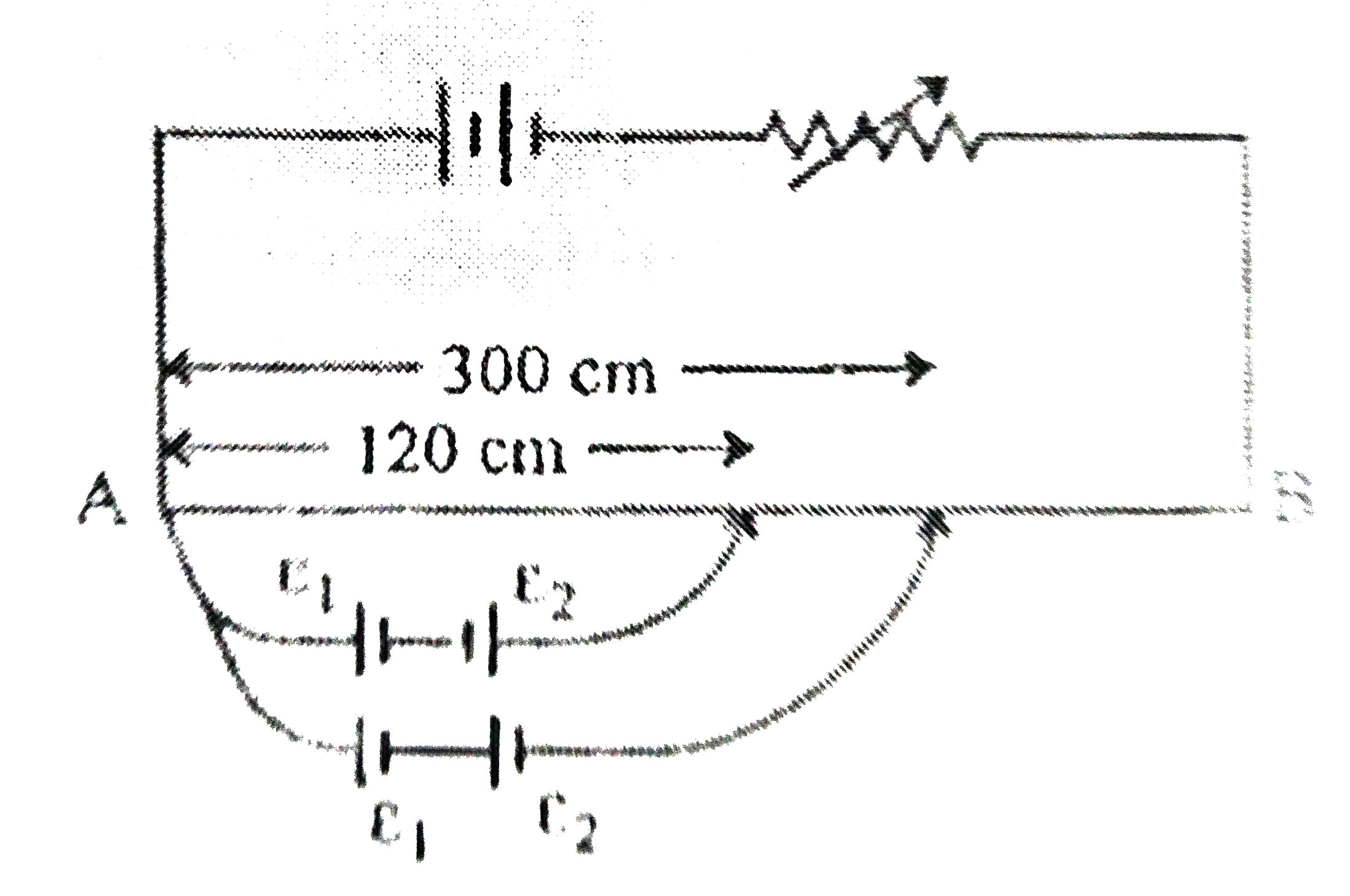
View SolutionTwo cells when connected in series are balanced on 6 m on a potentiometer. If the polarity one of these cell is reversed, they balance on 2m. The ratio of e.m.f of the two cells.
View SolutionIn a potentiometer, a uniform potential gradient of 0.8Vm−1 is maintained across its 10 m wire . The potential difference across two points on the wire located at 65 cm and 2.45 m is
View SolutionAB is a potentiometer wire of length 100 cm and its resistance is 10Ω. It is connected in series with a resistance R = 40 Ω and a battery of emf 2 V and negligible internal resistance. If a source of unknown emf E is balanced by 40 cm length of the potentiometer wire, the value of E is
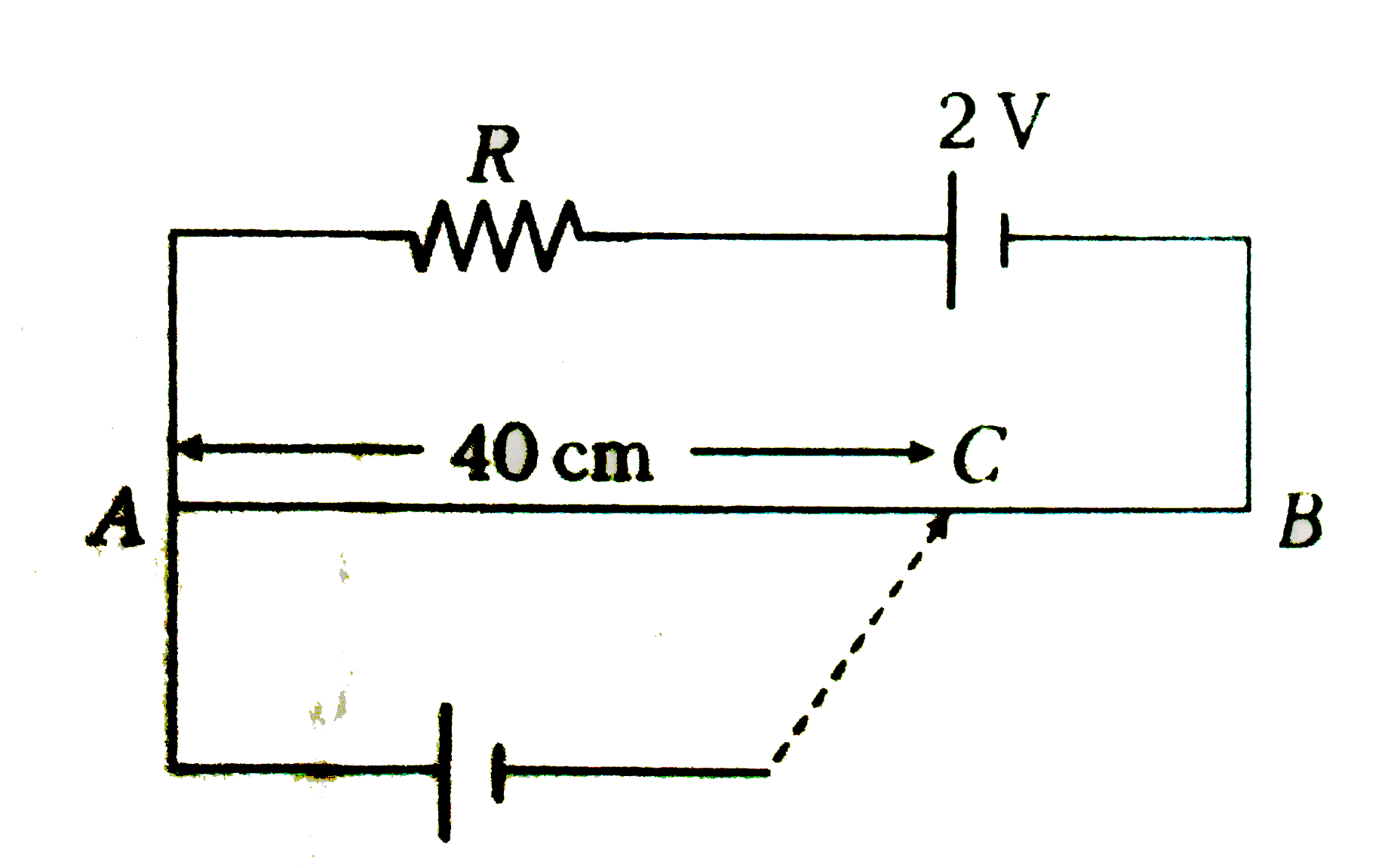
View Solution
