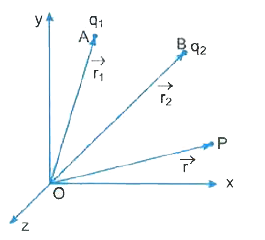
Deduce the expression for the electric filed $\to E$ due to a system of two charges $q_{1} and q_{2}$ with position vectors $\to r_{1} and \to r_{2}$ at a point P having position vector $\to ®$ .

Text Solution

Verified by Experts

Let as shown two point charges $q_{1} and q_{2}$ be situated at points A and B respectively with positions vectors $\to r_{1} and \to r_{2}$ . Let P be a point having position vector $\to ®$ . Electric field at P due to charge $q_{1}$
$- \to E_{1} = \frac{1}{4 π \in_{0}} . \frac{q_{1}}{{∣ ∣ \to r - \to r_{1} ∣ ∣}^{3}} . (\to r - \to r_{1})$
and field at P due to charge $q_{2}, - \to E_{2} = \frac{1}{4 π \in_{0}} . \frac{q_{2}}{∣ ∣ \to r - \to r_{2} ∣ ∣} (\to r - \to r_{1})$
$∴$ Total electric field at point P is
$\to E = - \to E_{1} + - \to E_{2} = \frac{1}{4 π \in_{0}} ⎡ ⎢ ⎢ ⎣ \frac{q_{1}}{{∣ ∣ \to r - \to r_{1} ∣ ∣}^{3}} . (\to r - \to r_{1}) + \frac{q_{2}}{∣ ∣ \to r - \to r_{2} ∣ ∣} ⎤ ⎥ ⎥ ⎦$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

U-LIKE SERIES-ELECTRIC CHARGES AND FIELDS -SHORT ANSWER QUESTIONS

Home
Ask Doubt
Profile