A simple pendulum consists of a small sphere of mass m suspended by a thread of length l. The sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically downwards. Finds the period of oscillation of the pendulum due to the electrostatic force acting on the sphere, neglecting the effect of the gravitational force.
Let the pendulum be be displaced from its equilibrium position A to position B through a small angle θ and then released. Forces acting on pendulum are (i) force F= qE in vertical downward direction due to the electrical field, and (ii ) the tension T0 and hence unbalanced restoring force is qE sinθ
if θ is small then sinθ=θ=arcAB1
∴ Restoring force =−qEθ=−qEl(areAB)
obviously the motion of pendulum is SHM ,whose time period is given as:
T=2π√inertia factor spring factor =2π√mqE/l=2π√mlqE
(##U_LIK_SP_PHY_XII_C01_E09_020_S01.png" width="80%">
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - LONG ANSWER QUESTIONS -I
30 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - LONG ANSWER QUESTIONS -II
9 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - VERY SHORT ANSWER QUESTIONS
39 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - U-LIKE SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - SELF ASSESSMENT TEST SECTION-C (VERY SHORT ANSWER QUESTIONS)
3 Videos
- ELECTROMAGNETIC WAVESBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SELF ASSESSMENT TEST (SECTION C)
1 Videos
Similar Questions
A simple pendulum consists of a small sphere of mass m suspended by a thread of length l. the sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically upwards. With what period will the pendulum oscillate if the electrostatic force acting on the sphere is less than the gravitational force?
View SolutionA simple pendulum consists of a small sphere of mass m suspended by a thread of length l. the sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically upwards. With what period will pendulum oscillate if the electrostatic force acting on the sphere is less than the gravitational force ?
View Solution
Knowledge Check
A Pendulum bob of mass m and charge q is suspended by a thread of length l. The pendulum is placed in a region of a uniform electric field E directed vertically upward. If the electristatic force acting on the sphere is les than that of gravitational fore, calculate the period with which the pendulum oscillates (Assumes small oscillation)
AT=2π ⎷lg+qEmBT=2π ⎷lg−qEmCT=π ⎷lg−qEmDT=π ⎷lg+qEmA simple pendulum has a length l & mass of bob m. The bob is given a charge q coulomb. The pendulum is suspended in a uniform horizontal electric field of strength E as shown in figure, then calculate the time period of oscillation when bob is slightly displaced from its mean position.
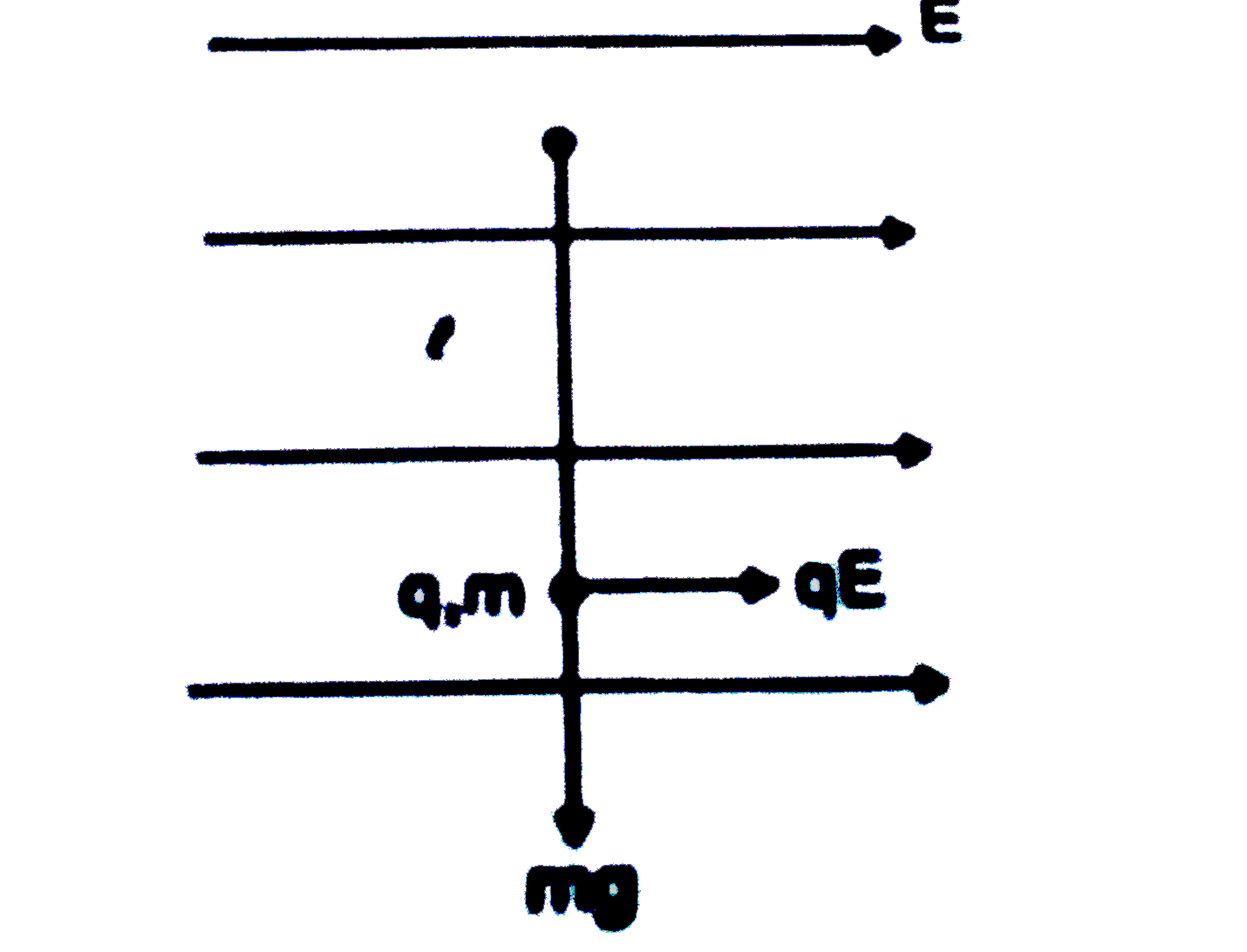 A2π√lgB2π ⎷⎧⎨⎩lg+qEm⎫⎬⎭C2π ⎷⎧⎨⎩lg−qEm⎫⎬⎭D2π ⎷l√g2+(qEm)2
A2π√lgB2π ⎷⎧⎨⎩lg+qEm⎫⎬⎭C2π ⎷⎧⎨⎩lg−qEm⎫⎬⎭D2π ⎷l√g2+(qEm)2A simple pendulum of mass m and charge +q is suspended vertically by a massless thread of length l. At the point of suspension, a point charge +q is also fixed. If the pendulum is displaced slightly from equilibrium position, its time period will be
AT=2π ⎷lg+kq2ml2BT=2πCT=2π√lgDwill be greater then 2π√lg
A simple pendulum consists of a small sphere of mass m suspended by a thread of length l. the sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically upwards. With what period will pendulum oscillate if the electrostatic force acting on the sphere is less than the gravitational force ?
View SolutionA simple pendulum has a length l & mass of bob m. The bob is given a charge q coulomb. The pendulum is suspended in a uniform horizontal electric field of strength E as shown in figure, then calculate the time period of oscillation when bob is slightly displaced from its mean position.

View SolutionA simple pendulum having caharge q1 mass ma and effective length 1, is suspended from a rigid support between the plates of charged horizontal capacitor. Electric field in the capacitor is perpendicular to the plates and directed vertically downwards .
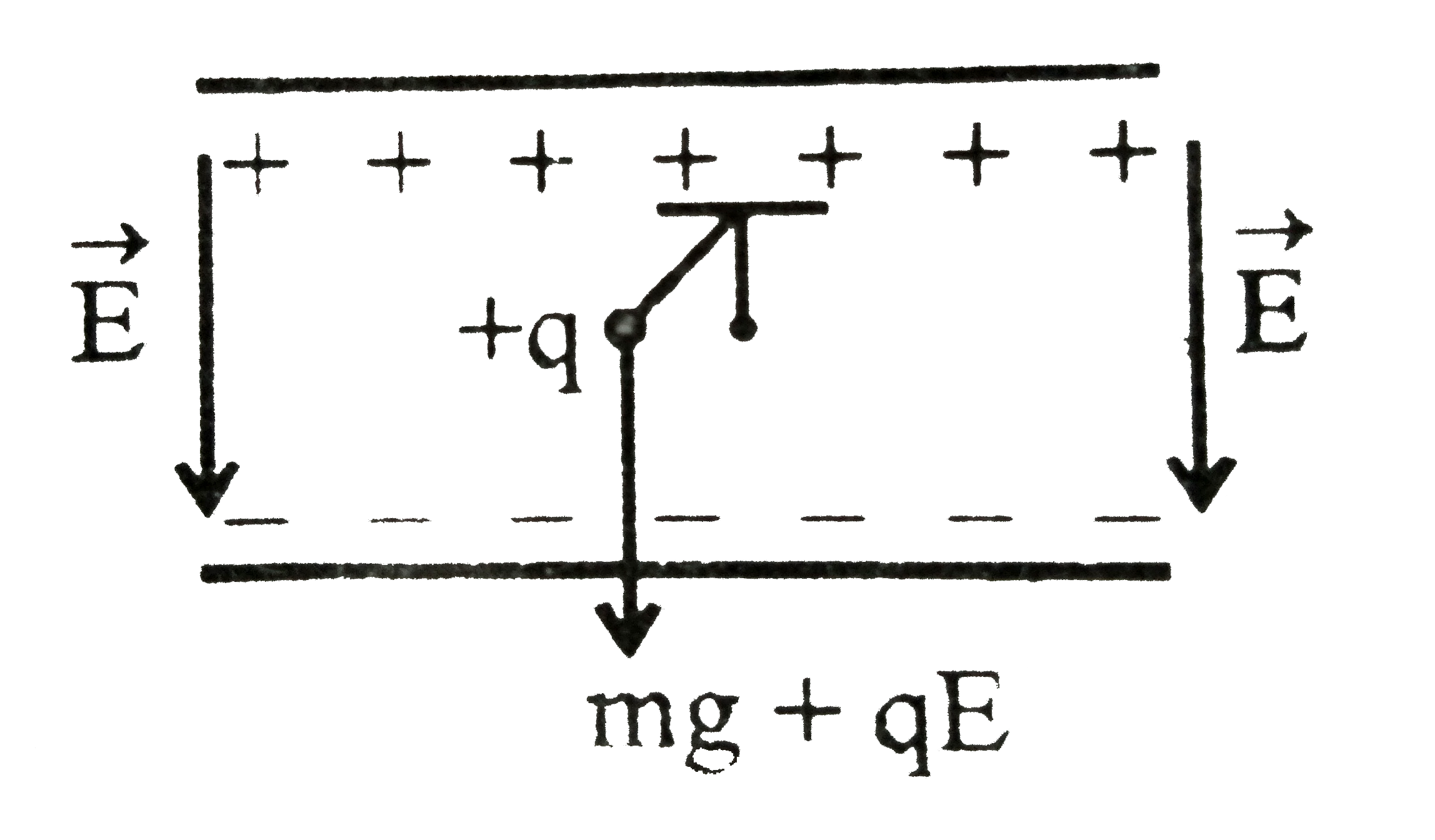
The time period of oscillation of the pendulum. if plates are held vertically , is given by :
View SolutionThe bob of a simple pendulum of length /has a positive charge q on it. The pendulum is fixed to a horizontally oriented positively charged sheet as shown in the figure. The time period of the small oscillations of simple pendulum is
View SolutionA simple pendulum having caharge q1 mass ma and effective length 1, is suspended from a rigid support between the plates of charged horizontal capacitor. Electric field in the capacitor is perpendicular to the plates and directed vertically downwards .
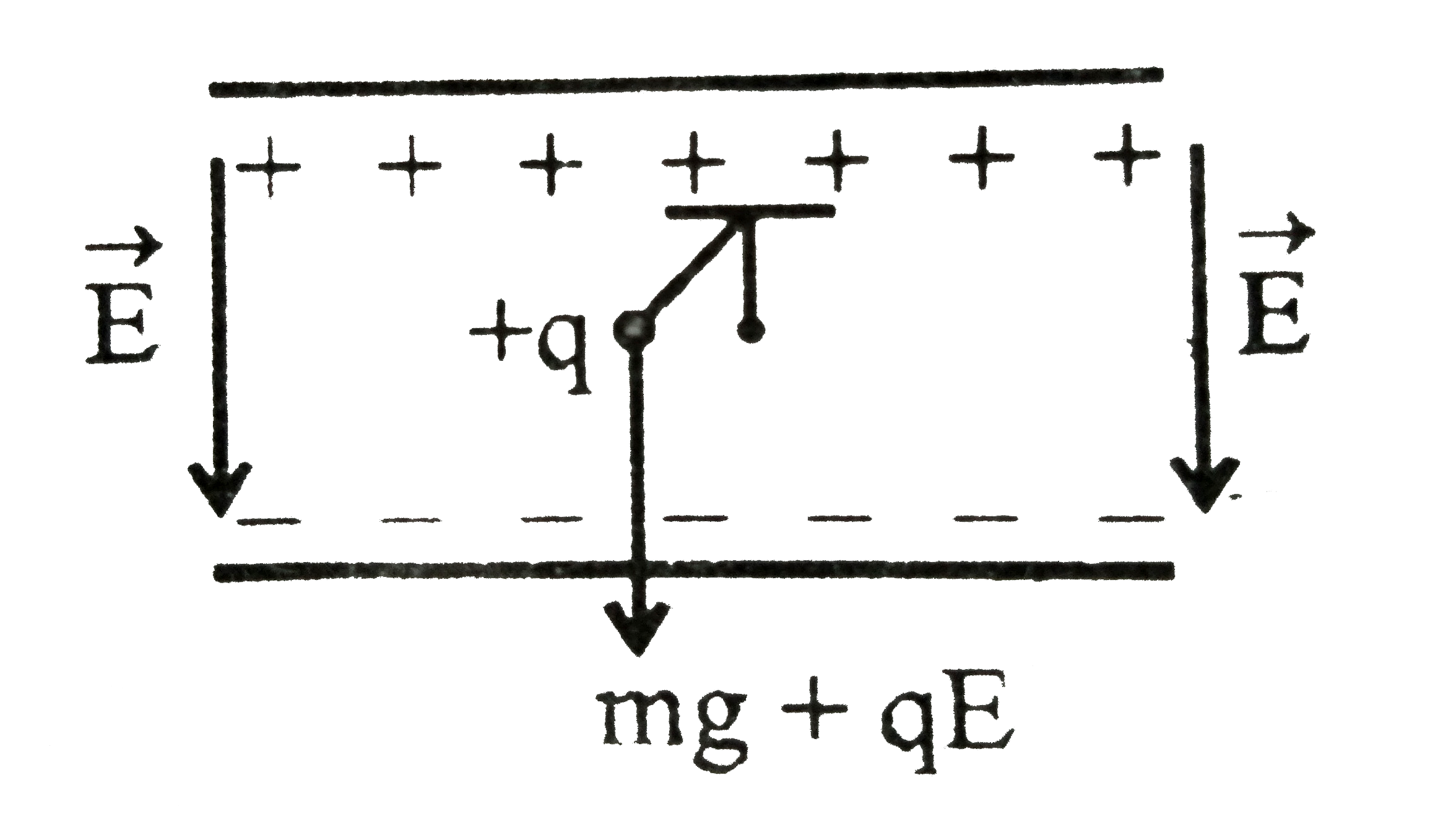
The time period of socillattion of the pendulum is given by :
View Solution
