Define vector product. Explain the properties of a vector product with two examples.
Text Solution
Vector product or cross product : If the product of two vectors (say ¯¯¯Aand¯¯¯B) gives a vector then that multiplication of vectors is cross product or vector product of vectors.
Mathematically ¯¯¯Aׯ¯¯B=∣∣¯¯¯A∣∣∣∣¯¯¯B∣∣sinθ.ˆn
Vector product is a unit vector perpendicular to both ¯¯¯Aand¯¯¯B or perpendicular to the plane of ¯¯¯Aand¯¯¯B.
Properties of cross product :
1. Cross product is not commutative i.e. ¯¯¯Aׯ¯¯B≠¯¯¯Bׯ¯¯A. But ¯¯¯Aׯ¯¯B=−¯¯¯Bׯ¯¯A
2. Cross product obeys distributive law i.e. ¯¯¯A×(¯¯¯B+¯¯¯C)=(¯¯¯Aׯ¯¯B)+(¯¯¯Aׯ¯¯C)
3. If any vector is represented by the combination of ¯i,¯jand¯k then cross product will obey right hand screw rule.
4. The product of two coplanar perpendicular unit vectors will generate a unit vector perpendicular to that plane i.e., ¯iׯj=¯k,¯jׯk=¯iand¯kׯi=¯j
5. Cross product of parallel vectors is zero i.e. ¯iׯi=¯jׯj=¯kׯk=0
Examples of cross product :
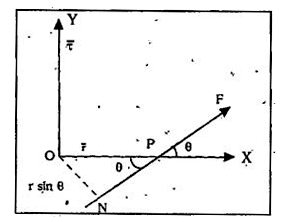
1. Torque or moment of force (¯τ) : Torque is defined as the product of force and perpendicular distance from the point of application.
Let a force ¯¯¯F act on a point P which is at a distance .r. from .O.. Let the Force ¯¯¯F act with some angle .θ.on¯¯¯¯¯¯OP
The perpendicular distance ON = ¯rsinθ
∴ Torque τ=¯rׯ¯¯F
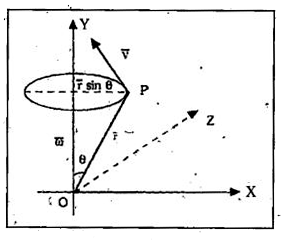
2. Angular momentum and angular velocity : Let a rigid body is rotating about the Y-axis with a constant angular velocity .ω. Consider a point .P. in the body which is at a distance ¯r from origin.
The velocity ¯v is perpendicular to both ¯¯ωand¯¯¯P
Velocity ¯v=→ω¯rsinθ
∴ Velocity ¯v=¯¯ωׯr
(OR) Angular momentum (¯¯¯L) = radius (¯r)× momentum (¯¯¯P)
∴ Angular momentum (¯¯¯L)=¯r×(m¯v)=m(¯rׯv)
|
Topper's Solved these Questions
- MODEL PAPER 5BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 5EXERCISE - SECTION - C
3 Videos
- MODEL PAPER 5BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 5EXERCISE - SECTION - C
3 Videos
- MODEL PAPER 4 BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 4 EXERCISE - SECTION -C
3 Videos
- MODEL PAPER 6BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 6EXERCISE - SECTION - C
3 Videos
Similar Questions
Write any three properties of vector product of two vectors .
View SolutionProperties Of Vector Cross Product
View SolutionDefine vector product of two vectors.
View SolutionDefine vector product of two vectors.
View SolutionDefine vector product. Describe vector product of two vectors with at least two examples. Mention the properties of vector product.
View SolutionScalar product OF vector & properties
View SolutionDefine scalar product Describe the scalar product with two examples. Also mention the properties of scalar product.
View SolutionWhat is vector product of two vectors ? Give two examples .
View SolutionWhat is scalar product of two vectors ? Give two examples .
View SolutionCross product of two vectors is called vector product .Why?
View Solution
