Define wavefront of a travelling wave. Using Huygens principle, obtain the law of refraction at a plane interface when light passes from rarer to a denser medium.

Text Solution

Verified by Experts

A wavefront is a surface of constant phase.
Consider a plane surface XY separating a rarer medium of refractive index $n_{1}$ from a denser medium of refractive index $n_{2}$ . Let $c_{1} and c_{2}$ be the values of speed of light in the two media. AB is a plane wavefront incident on XY at an angle i. Let at a given instant the end of wavefront just strikes the surface XY but the other end B has still to cover a path BC. If it takes time t, then $B C = c_{1} t .$
According to Huygen.s principle, point A meanwhile begins to emit secondary wavelength which will cover a distance $c_{2} t$ in second medium in time t. Draw a circular arc with A as centre and $c_{2} t$ at as radius and draw a tangent CD from point C on this arc. Then CD is the refracted wavefront, which subtends an angle r from surface XY.

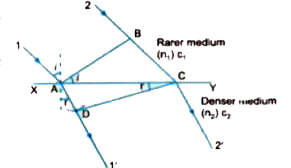
Now in $△ A B C sin i = \frac{B C}{A C} = \frac{c_{1} t}{A C}$
and in $△ A D C sin r = \frac{A D}{A C} = \frac{c_{2} t}{A C}$
$\frac{sin i}{sin r} = \frac{c_{1} t / A C}{c_{2} t / A C} = \frac{c_{1}}{c_{2}} = a constant = \frac{n_{2}}{n_{1}} = n_{21}$
Which is Snell.s law of refraction.

Updated on:21/07/2023

When light passes from a denser medium to a rarer medium
AVelocity of light increases
BVelocity of light decreases
CVelocity of light remains unchanged
DVelocity of light becomes infinity
When light travels from a rarer medium to a denser medium, it ________
Aspeed remains the same
Bspeeds down then up
Cspeeds down
Dspeeds up