Question

Using Huygen.s principle, verify Snell.s law of refraction of plane wave propagating from denser medium to rarer medium.

Explanation

To verify Snell's law of refraction using Huygens' principle, we will follow these steps:

Step 1: Understanding Huygens' Principle
Huygens' principle states that every point on a wavefront can be considered as a source of secondary wavelets, and the new wavefront is the envelope of these wavelets.

Step 2: Setting Up the Problem
Consider two media: a denser medium (medium 1) with refractive index \( \mu_1 \) and a rarer medium (medium 2) with refractive index \( \mu_2 \). According to the problem, \( \mu_1 > \mu_2 \). We will analyze the wavefronts and rays at the interface between these two media.

Step 3: Drawing the Incident Wavefront and Rays
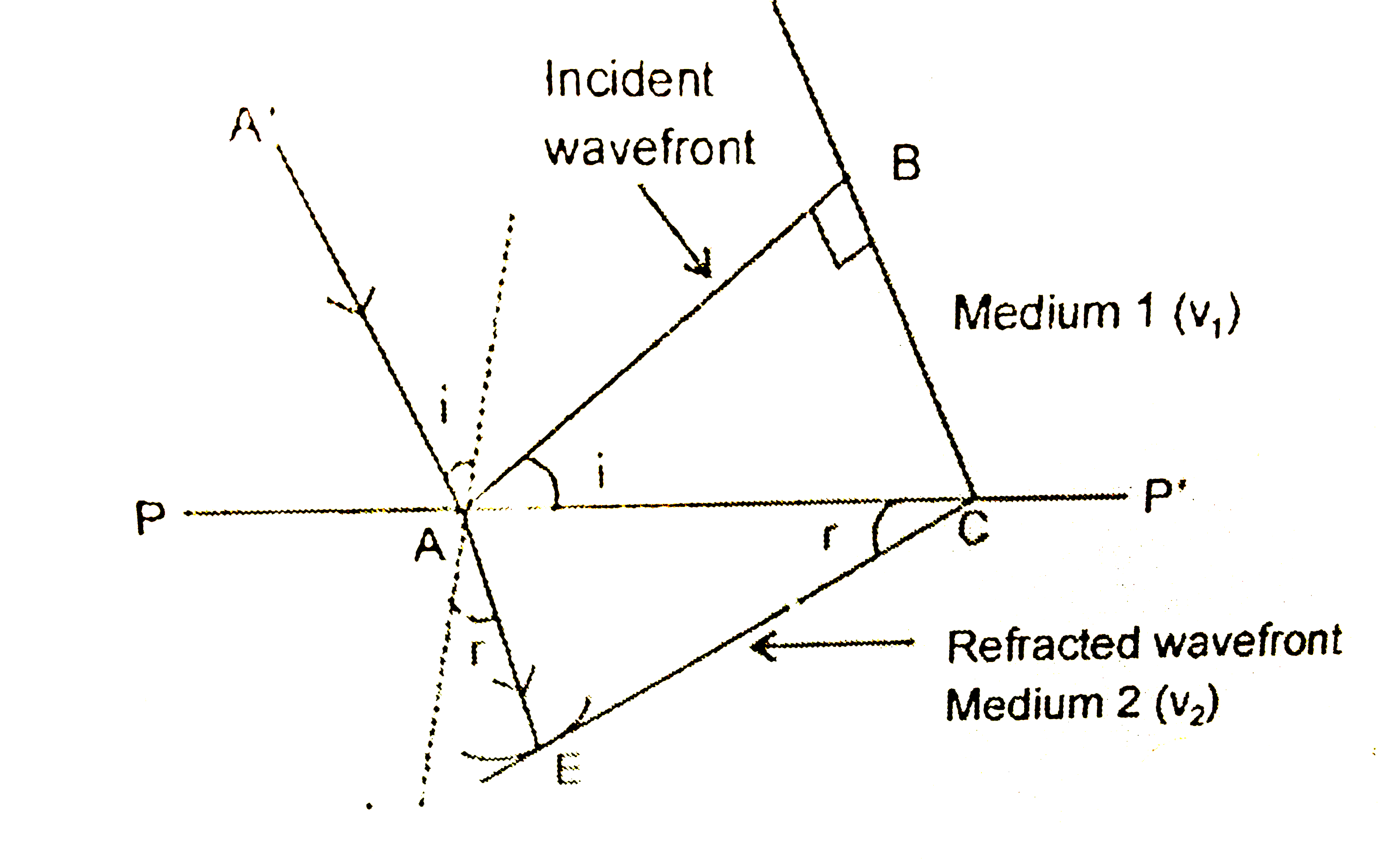
- Draw the interface between the two media.
- Draw an incident ray from the denser medium making an angle of incidence \( I \) with the normal to the interface.
- Draw the corresponding incident wavefront perpendicular to the incident ray.

Step 4: Identifying the Refraction
As the wave travels from the denser medium to the rarer medium, it bends away from the normal. Draw the refracted ray making an angle of refraction \( R \) with the normal.

Step 5: Constructing the Wavefronts
- Draw the incident wavefronts parallel to each other, and label them.
- Draw the refracted wavefronts, which will also be parallel to each other and perpendicular to the refracted rays.

Step 6: Time Calculation
Using the wavefronts, we can analyze the time taken for the wave to travel from point A (on the incident wavefront) to point F (on the refracted wavefront) and compare it to the time taken to travel from point D to point B and from point E to point C.

Step 7: Expressing Time in Terms of Distance and Velocity
The time taken to travel a distance is given by:
\( T = \frac{\text{Distance}}{\text{Velocity}} \)
For the first medium:
\( T_{AF} = \frac{AF}{V_1} \)
For the second medium:
\( T_{EC} = \frac{EC}{V_2} \)

Step 8: Relating Distances to Angles
Using trigonometric relationships in the triangles formed by the rays and the normals:
- For the triangle AEC:
\( \sin I = \frac{AC}{AE} \)
- For the triangle FBC:
\( \sin R = \frac{AF}{AC} \)

Step 9: Setting Up the Equation
From the above relationships, we can express:
\( AF = AC \cdot \sin R \)
\( EC = AC \cdot \sin I \)

Step 10: Equating the Times
Since the time taken is the same, we can set:
\( \frac{AC \cdot \sin R}{V_1} = \frac{AC \cdot \sin I}{V_2} \)

Step 11: Simplifying the Equation
Canceling \( AC \) from both sides gives:
\( \frac{\sin I}{\sin R} = \frac{V_1}{V_2} \)

Step 12: Relating Velocities to Refractive Indices
Using the relationship between velocity and refractive index:
\( V_1 = \frac{C}{\mu_1} \quad \text{and} \quad V_2 = \frac{C}{\mu_2} \)
Substituting these into the equation gives:
\( \frac{\sin I}{\sin R} = \frac{\mu_2}{\mu_1} \)

Step 13: Conclusion
This is Snell's law of refraction, which states:
\( \mu_1 \sin I = \mu_2 \sin R \)
Thus, we have verified Snell's law using Huygens' principle.

---