Derive an expression for capacitance of a parallel plate capacitor. Solution in Punjabi
Capacitor : An arrangement of two metallic conductors separated by some non conducting medium which can store large amount of charge in small space is called a capacitor.
Capacitor is also known as a condenser.
,
Di-electrics : Those non-conducting materials in which equal and opposite induced charges are produced on their opposite faces, when electric field is applied, are called dielectrics.
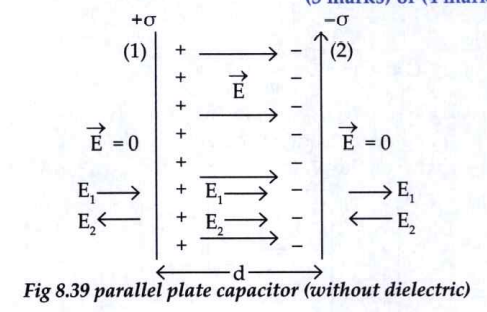
Capacitance of a parallel plate capacitor having vacuum (or air) between the plates of the capacitor is given by-
,
where A - Area of each plate
d = Distance or separation between the plates of a capacitor
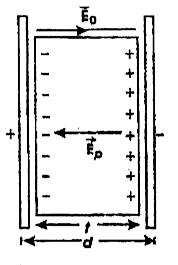
Now, let us introduce a dielectric slab of thickness .t. between the plates of the capacitor.
Due to polarization, equal and opposite induced charges appear on the two faces of the dielectric slab. These induced charges give rise to induced electric field () which is in a direction opposite to the applied field . The reduced
value of the electric field in the dielectric, .
Now, exists in a region of thickness .t. and field exists in a region of thickness (d - t).
Potential difference between the two plates of the capacitor
is given by:
Since, or
......(2)
We know, [
Eqn (2) becomes ......(3)
Now, Capacitance of the capacitor
or
Clearly,
So when a dielectric slab is introduced.between the plates of a parallel plate capacitor, then its capacity increases.
If the dielectric fills the whole space between the plates of a capacitor i.e., t = d
Then
The capacity of a capacitor increases by dielectric constant (K) times.
Topper's Solved these Questions
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - CAPACITANCE EXERCISE - LONG ANSWERTYPE QUESTIONS (5/6 Marks Questions)16videos
CAPACITANCE
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - CAPACITANCE EXERCISE - NUMERICAL PROBLEMS21videos
CAPACITANCE
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - CAPACITANCE EXERCISE - SHORT ANSWERTYPE QUESTIONS (2 Marks Questions)5videos
CAPACITANCE
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ALTERNATING CURRENTS EXERCISE - MOST EXPECTED QUESTIONS11videos
ALTERNATING CURRENTS
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - CLASSIFICATION OF MATERIALSEXERCISE - Most expected question (2 marks)3videos
CLASSIFICATION OF MATERIALS
Similar Questions
Derive an expression for capacitance of a parallel plate capacitor.
03:35View SolutionA parallel plate capacitor with air between the plates has a capacitance of 8 pF. The separation between the plates is now reduced by half and the space between them is filled with a medium of dielectric constant K. Calculate the value of the capacitance of the capacitor in the second case.
12:22View SolutionFind an expression for the capacity of a metallic sphere.
03:51View SolutionWhat is a phasor?
View SolutionDoes the magnetisation of a paramagnetic salt dependon temperature ? Give reason for your answer.
02:48View SolutionDerive an expression for the capacitance of a parallel-plate capacitor filled with a dielectric.
04:34View Solutionसंधारित्र की धारिता की परिभाष लिखिए। समांतर-प्लेट संधारित्र की धारिता का व्यंजक व्युत्पादित कीजिए। इसकी धारिता कैसे बड़े जा सकती है?
05:39View SolutionDerive an expression for the capacitance of a parallel plate capacitor.
06:08View SolutionDerive an expression for the capacitance of a parallel plate capacitor. Explain the effect of dielectrics on capacitance of this capacitor. Or. Derive expression for capacitance of a parallel plate capacitor. Explain the effect of dielectrics on its capacitance.
06:00View SolutionObtain the expression for capacitance for capacitance for a parallel plate capacitor .
10:03View SolutionDerive an expression for capacitance of a paralle plate capacitor
04:16View SolutionDerive expression for the capacitance of the parallel plate capacitor,
02:43View SolutionDerive an expression for the capacitance of a parallel plate capacitor with dielectric as the medium between the plates.
05:48View SolutionWhat is a capacitor? Derive an expression for capacitance of a parallel plate capacitor.
06:08View SolutionDefine the capacitance of capacitor. Derive an expression for the capacity of parallel plate capacitor with a dielectric slab placed in between the plates of capacitor.
View SolutionDerive an expression for capacitance of a parallel plate capacitor without a dielectric.
 View Solution
View Solution

