Question

Derive an expression for the acceleartion of the body sliding down a frictionless surface

Explanation

When an object of mass m slides on a frictional surface inclined at an angle `theta` as shown in the figure the forces acting on it decides the acceleration of the object (b) speed of the object when it reaches the bottom .

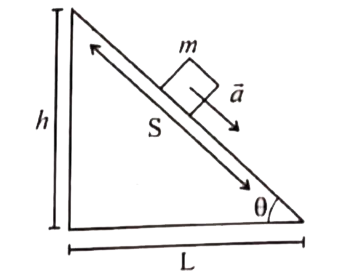
The force acting on the object is
(i) Downward gravitational force (mg)
(ii) Normal force perpendicular to inclined surface (N)
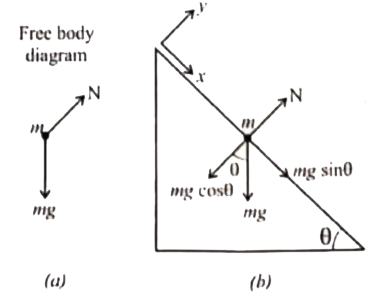
the block is assumed to be a point mass [In order to draw the free body diagram in figure (a)]. Since the motion is on the inclined surface the coordinate system parallel to teh inclined surface is chosen as shown in the figure (b) It is noted that the angle made by the gravitational force with the perpendicular to the surface si equal to the angle of inclination `theta` as shown in in figure
`-mg cos theta hat(j) + N hat(j) = 0` (No acceleration )
By comparing the components on both sides N- mg cos `theta = 0`
`N= mg cos theta`
The magnitude of normal force (N) exerted by tghe surface is equivalent to mg cos `theta` . The object slides along the x direction .
By comparing the components on both sides we can equate
`mg sin theta = ma `
The acceleration of the slinding object is


Note that the acceleratin depends on the angle inclination `theta`