Derive an expression for the magnetic induction at a point on the axial line of a bar magnet.
To derive the expression for the magnetic induction at a point on the axial line of a bar magnet, we will follow these steps:
1. Understanding the Setup:
- Consider a bar magnet with a north pole (N) and a south pole (S). Let the length of the magnet be L.
- Let the distance from the center of the magnet to the point P on the axial line be r.
2. Defining Pole Strength:
- Let the pole strength of both the north and south poles be m.
3. Magnetic Field Due to the North Pole:
- The magnetic field BN at point P due to the north pole is given by:
BN=μ04π⋅m(r−L2)2
- Here, (r−L2) is the distance from the north pole to point P.
4. Magnetic Field Due to the South Pole:
- The magnetic field BS at point P due to the south pole is given by:
BS=μ04π⋅m(r+L2)2
- Here, (r+L2) is the distance from the south pole to point P.
5. Net Magnetic Field:
- The net magnetic field B at point P is the difference between the fields due to the north and south poles:
B=BN−BS
- Substituting the expressions for BN and BS:
B=μ04π⎛⎝m(r−L2)2−m(r+L2)2⎞⎠
6. Finding a Common Denominator:
- To simplify the expression, find a common denominator:
B=μ0m4π⎛⎝(r+L2)2−(r−L2)2(r−L2)2(r+L2)2⎞⎠
7. Expanding the Numerator:
- Expanding the numerator using the difference of squares:
(r+L2)2−(r−L2)2=4r⋅L2=2rL
8. Final Expression:
- Substitute back into the equation for B:
B=μ0m4π⋅2rL(r−L2)2(r+L2)2
- For large r (where r≫L), we can approximate:
B≈μ0⋅2m4πr3
Final Result:
The expression for the magnetic induction at a point on the axial line of a bar magnet is:
B=μ0⋅m2πr3
- Consider a bar magnet with a north pole (N) and a south pole (S). Let the length of the magnet be L.
- Let the distance from the center of the magnet to the point P on the axial line be r.
- Let the pole strength of both the north and south poles be m.
- The magnetic field BN at point P due to the north pole is given by:
BN=μ04π⋅m(r−L2)2
- Here, (r−L2) is the distance from the north pole to point P.
- The magnetic field BS at point P due to the south pole is given by:
BS=μ04π⋅m(r+L2)2
- Here, (r+L2) is the distance from the south pole to point P.
- The net magnetic field B at point P is the difference between the fields due to the north and south poles:
B=BN−BS
- Substituting the expressions for BN and BS:
B=μ04π⎛⎝m(r−L2)2−m(r+L2)2⎞⎠
- To simplify the expression, find a common denominator:
B=μ0m4π⎛⎝(r+L2)2−(r−L2)2(r−L2)2(r+L2)2⎞⎠
- Expanding the numerator using the difference of squares:
(r+L2)2−(r−L2)2=4r⋅L2=2rL
- Substitute back into the equation for B:
B=μ0m4π⋅2rL(r−L2)2(r+L2)2
- For large r (where r≫L), we can approximate:
B≈μ0⋅2m4πr3
The expression for the magnetic induction at a point on the axial line of a bar magnet is:
B=μ0⋅m2πr3
Topper's Solved these Questions
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - EXERCISE (VERY SHORT ANSWER QUESTIONS)
25 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - PROBLEMS (LEVEL-I)
21 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - EXERCISE (LONG ANSWER QUESTIONS )
6 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)
7 Videos
Similar Questions
Derive an expression for the magnetic field at a point on the axis located at a distance x from the centre of a magnetic dipole of length 2l and magnetic moment M.
View SolutionMatch the following :

View Solution(a) Draw the equipotential surfaces corresponding to a uniform electric field in the z-direction.
(b) Derive an expression for the electric potential at any point along the axial line of an electric dipole
View SolutionDerive the expression for the electric potential at any point along the axial line of an electric dipole.
View SolutionUsing Biot-Savart’s law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
View SolutionThe magnetic induction at centre O Fig.
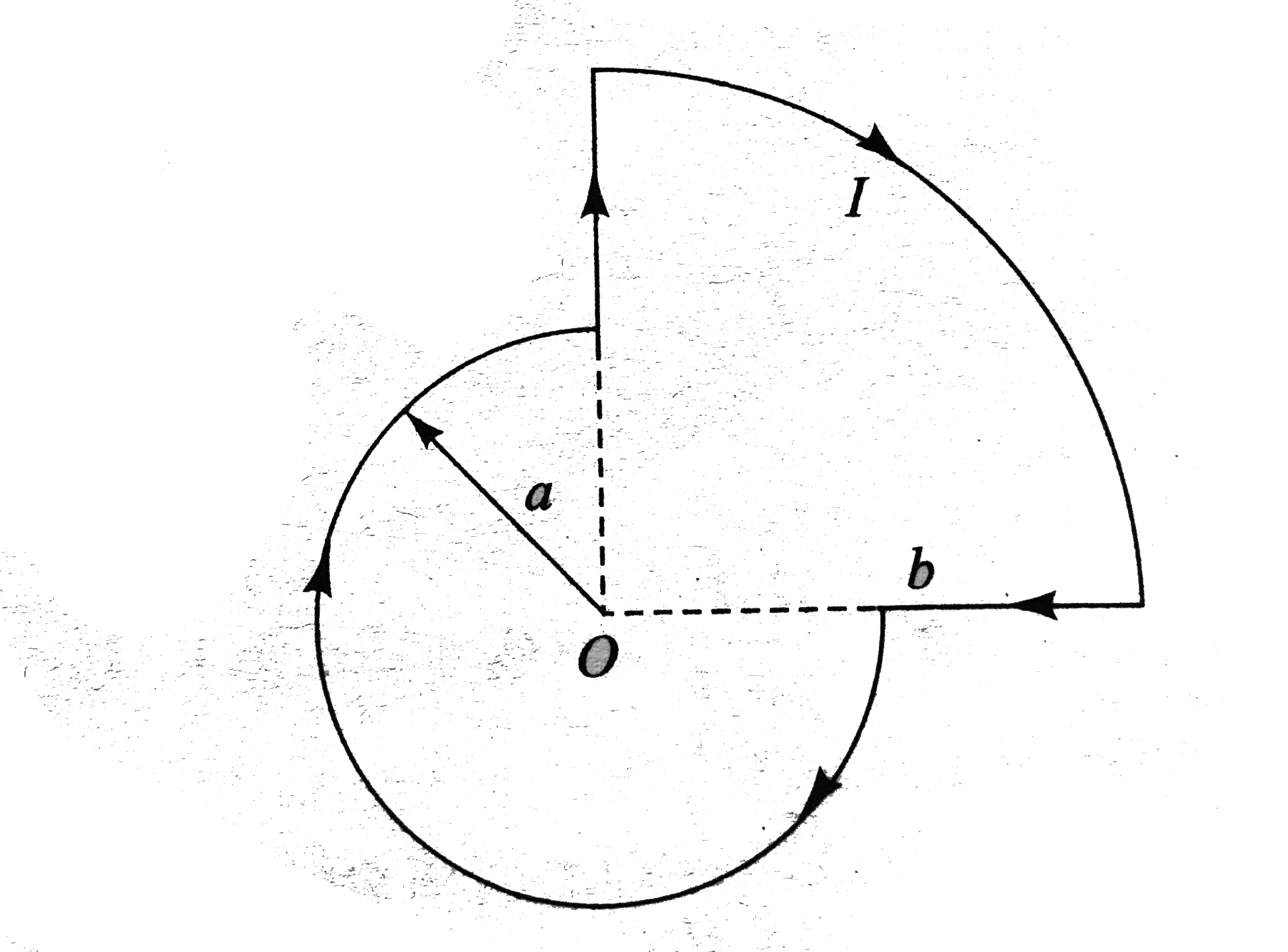
View SolutionMagnetic induction at the point O in the adjacent figure is
View SolutionMagnetic length of a bar magnet is
View SolutionUnit of magnetic induction field B is
View SolutionThe magnetic induction at the point O, if the wire carries a current I, is

View Solution
