Derive an expression for the pressure of an ideal gas in a container from Kinetic Theory and hence give Kinetic Interpretation of Temperature.
Text Solution
Consider a cube of side .l. and an ideal gas is filled in it. Let the co-ordinates, X, Y and Z will coincide with the sides of the cube. Let velocities of gas molecules along these directions are Vx,VyandVz. Consider a gas molecule moving along X-axis with a velocity Vx. Its motion is perpendicular to Y-Z plane. Let the gas molecule suffered elastic collision with Y-Z plane and bounced back. In this case the velocities VyandVz are not considered because collision is along X-direction only.
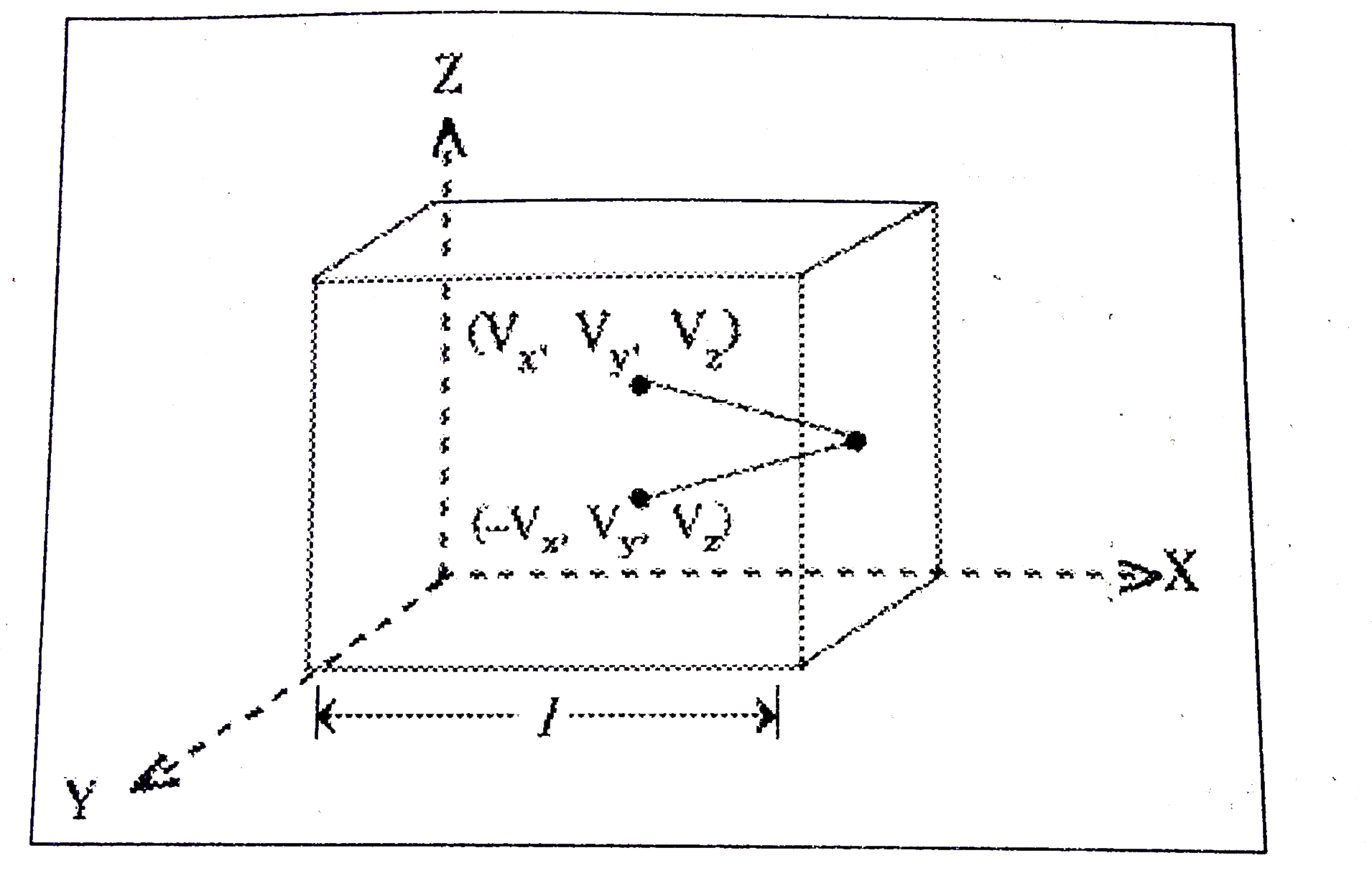
Change in momentum along X-direction is final momentum (−mVx) - initial momentum (mVx)=−2mVx ...........(1)
Let area of one side of the cube is A. Then during the time Δt only the molecules at a distance of VxΔt will collide with the walls. Let number of gas molecules in the volume AVΔt are say.n.. In these molecules half of the molecules will move towards the wall and remaining will move away from the wall.
∴ Amount of momentum transferred to the wall = Q
=2mVx× number of molecules collided with wall
∴Q=2mVx(12nAVxΔt)
Pressure on Y - Z plane =
Px=Rate of change in momentumArea
∴P=ForceArea=Q/ΔtA
=2mVx.12nAVxΔtAΔt=nmV2x
If behaviour of gas is isotropic that is equal in all directions then Vx=Vy=Vz
∴ Root mean square velocity of gas
=V2x+V2y+V2z3=13¯¯¯V2
Where ¯¯¯V2=V2x+V2y+V2z
∴ Pressure of gas P=13nm¯¯¯V2
From Pascal.s law pressure is same throught the container so pressure in any direaction (say x,y or z) is same.
Kinetic interpretation of temperature :
From gas equation
PV=13nm¯¯¯V2.V=23N(12)m¯¯¯V2)
Where N=nV and 12m¯¯¯V2 = kinetic energy
for ideal gas internal energy is purely kinetic energy.
∴E=n12m¯¯¯V2∴PV=32E
But P=KBNT
∴E=32PV=32KBN.T
But EN=12mV2andEN=32KBT
∴ENαT is the average kinetic energy of gas molecule is proportional to absolute temperature of gas. But it does not depend on volume of container.

|
Topper's Solved these Questions
- KINETIC THEORYBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - KINETIC THEORYEXERCISE - Additional Problems
5 Videos
- KINETIC THEORYBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - KINETIC THEORYEXERCISE - Short Answer Questions
10 Videos
- HUMAN EYE AND COLOURFUL WORLDBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - HUMAN EYE AND COLOURFUL WORLDEXERCISE - CREATIVE QUESTIONS FOR NEW MODEL EXAMINATION (SECTION-IV) (APPLICATION TO DAILY LIFE, CONCERN TO BIODIVERSITY)
1 Video
- LAWA OF MOTIONBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - LAWA OF MOTIONEXERCISE - ADDITIONAL PROBLEMS
22 Videos
Similar Questions
Knowledge Check
Kinetic theory of an ideal gas gives the relation
A13nmV2B12nm¯v2CPV=μRTDNone of theseAn ideal gas obeying the kinetic theory of gases can be liquefied if
AIts temperature is more than its critical temperature (Tc)BIts pressure is more than its critical pressure (Pc)CIts pressure is more than Pc at a temperature less than TcDIt cannot be liquefied at any value of P and TAn ideal gas obeying the kinetic theory of gases can be liquefied if
AIts temperature is more than its critical temperature (Tc)BIts pressure is more than its critical pressure (Pc)CIts pressure is more than Pc at a temperature less than TcDIt cannot be liquefied at any value of P and T
Explain the kinetic interpretation of temperature
View SolutionWhat is the kinetic interpretation of temperature?
View SolutionWhat is the kinetic interpretation of temperature?
View SolutionAn ideal gas obeying the kinetic theory of gases can be liquefied if
View SolutionAn ideal gas obeying the kinetic theory of gases can be liquefied if
View Solution
