Question

Derive th lens maker's formula.

Explanation

Lens maker.s formula,
Let `r_1` and `r_2` be the radii of curvature of the thin lens.
Let O be the point object at a distance u from the pole of the first curved surface of the lens. Real image is formed at I., at a distance v from the pole `P_1`. This image is formed in the denser medium.

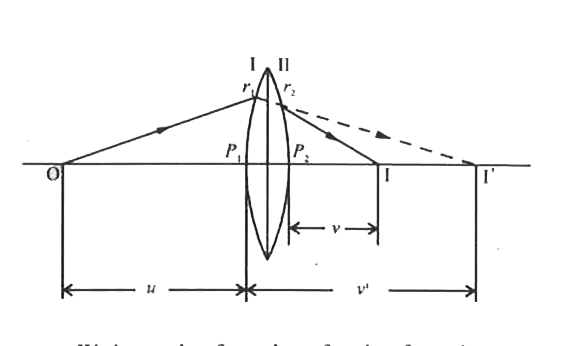
We know that from the refraction formula,
`n_1/(-u) + n_2/v = (n_2-n_1)/r`
i.e., `n_1/(-u) + n_2/(v.) =(n_2-n_1)/r_1` ....(1)
where `n_1` is the refractive index of rarer medium and `n_2` that of the denser medium `(n_2 > n_1)`. For the second surface, real image at I will serve as a virtual object and the distance is taken as -of. The object space is the lens medium for refraction through the second curved surface.
Final image is formed in air at I and at a distance of .v. from `P_2` .

`n_1/(-u) + n_2/v = (n_2-n_1)/ r`
i.e. , `n_2/(-v.)+ n_1/v =(n_2-n_1)/(-r_2)`...(2)
Adding (1) and (2) we get
`n_1/(-u) + n_1 /v = (n_2-n_1) (1/r_1 -1/r_2)`
or `1/(-u)+1/v =(n_2-n_1)/n_1 (1/r_1 -1/r_2)` ....(3)
when `u=oo , v=f `,
when u=f , v=`oo`
`therefore ` The term on the L.H.S. can be replaced by `1/f`
where f is the focal length of lens .
i.e., `1/f =((n_2-n_1)/n_1) (1/r_1 -1/r_2)` ...(4)
The equation (4) is called the lens maker.s formula.
Note:
(1) Using the equation (4), it can be shown that
`._1n_2 = 1-[(r_1r_2)/(f(r_1-r_2))]`
where, `._1n_2 =n_2/n_1 `
(2) For radius of curvature the letter .R. may be used.