Derive the expression for the power dissipated by an ideal resistor in an AC circuit .
To derive the expression for the power dissipated by an ideal resistor in an AC circuit, we can follow these steps:
Step 1: Define Instantaneous Power
The instantaneous power (P) in an AC circuit is given by the product of instantaneous voltage (V) and instantaneous current (I):
P(t)=V(t)⋅I(t)
Step 2: Express Voltage and Current
For an AC circuit, the instantaneous voltage and current can be expressed as:
V(t)=V0sin(ωt)
I(t)=I0sin(ωt+ϕ)
where V0 is the peak voltage, I0 is the peak current, ω is the angular frequency, and ϕ is the phase difference between the voltage and current.
Step 3: Substitute Voltage and Current into Power Equation
Substituting the expressions for voltage and current into the power equation gives:
P(t)=V0sin(ωt)⋅I0sin(ωt+ϕ)
Step 4: Use Trigonometric Identity
Using the trigonometric identity for the product of sines:
sinAsinB=12(cos(A−B)−cos(A+B))
we can rewrite the power equation:
P(t)=V0I02(cos(ϕ)−cos(2ωt+ϕ))
Step 5: Average Power Over a Complete Cycle
To find the average power over a complete cycle, we need to average P(t) over one complete cycle (T):
Pavg=1T∫T0P(t)dt
The term cos(2ωt+ϕ) averages to zero over one complete cycle, leaving:
Pavg=V0I02cos(ϕ)
Step 6: Express in Terms of RMS Values
The RMS (Root Mean Square) values of voltage and current are defined as:
Vrms=V0√2
Irms=I0√2
Substituting these into the average power expression gives:
Pavg=VrmsIrmscos(ϕ)
Step 7: Special Case for an Ideal Resistor
For an ideal resistor, the phase difference ϕ=0 (voltage and current are in phase). Therefore, cos(0)=1:
Pavg=VrmsIrms
Final Expression
Thus, the power dissipated by an ideal resistor in an AC circuit is:
P=VrmsIrms
The instantaneous power (P) in an AC circuit is given by the product of instantaneous voltage (V) and instantaneous current (I):
P(t)=V(t)⋅I(t)
For an AC circuit, the instantaneous voltage and current can be expressed as:
V(t)=V0sin(ωt)
I(t)=I0sin(ωt+ϕ)
where V0 is the peak voltage, I0 is the peak current, ω is the angular frequency, and ϕ is the phase difference between the voltage and current.
Substituting the expressions for voltage and current into the power equation gives:
P(t)=V0sin(ωt)⋅I0sin(ωt+ϕ)
Using the trigonometric identity for the product of sines:
sinAsinB=12(cos(A−B)−cos(A+B))
we can rewrite the power equation:
P(t)=V0I02(cos(ϕ)−cos(2ωt+ϕ))
To find the average power over a complete cycle, we need to average P(t) over one complete cycle (T):
Pavg=1T∫T0P(t)dt
The term cos(2ωt+ϕ) averages to zero over one complete cycle, leaving:
Pavg=V0I02cos(ϕ)
The RMS (Root Mean Square) values of voltage and current are defined as:
Vrms=V0√2
Irms=I0√2
Substituting these into the average power expression gives:
Pavg=VrmsIrmscos(ϕ)
For an ideal resistor, the phase difference ϕ=0 (voltage and current are in phase). Therefore, cos(0)=1:
Pavg=VrmsIrms
Thus, the power dissipated by an ideal resistor in an AC circuit is:
P=VrmsIrms
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Revision Exercises (Long Answer Questions )
10 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Revision Exercises (Nuumerical problems )
18 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Revision Exercises (Fill in the Blanks )
10 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
Similar Questions
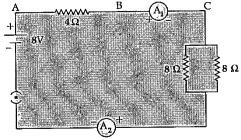
Power dissipated in 4Ω resistor is :
View SolutionA voltage V=Vmsinωt is applied to a series L-C-R circuit. Derive the expression for the average power dissipated over a cycle. Under what condition (i) no power is dissipated even though the current flows through the circuit, (ii) maximum power is dissipated in the circuit ?
View Solution
Knowledge Check
The power dissipated 6Ω resistor is
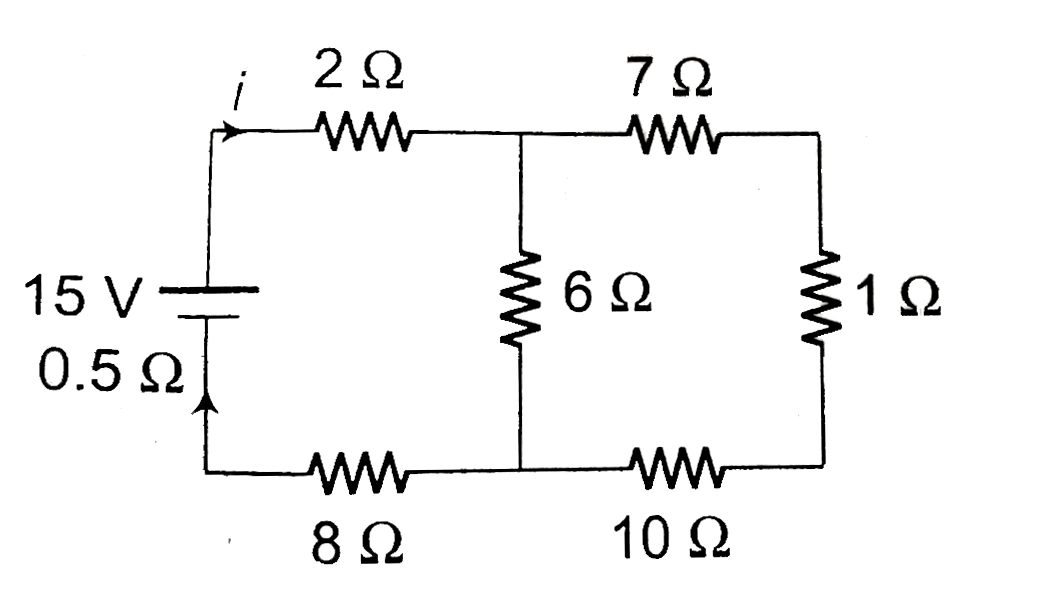 A278WB916WC616WD316W
A278WB916WC616WD316WThe average power dissipation in a pure capacitance in AC circuit is
A12CV2BCV2C14CV2DZero
The average power in LCR series circuit is
View SolutionA voltage V=V0sinωt is applied to a series LCR circuit. Derive expression for the average power dissipated over a cycle.
Under What condition (i) no power is dissipated even though the current flows through the circuit?
(ii) Maximum power is dissipated in the circuit?
View SolutionThe power dissipated in the adjacent circuit is -
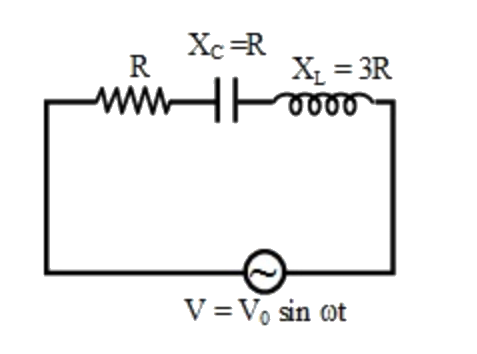
View SolutionDerive an expression for the impedance of an a.c. circuit consisting of an inductor and a resistor.
View SolutionDerive an expression for the impedance of an a.c. circuit consisting of an inductor and a resistor.
View SolutionThe power dissipated in the following circuit is
View Solution
