A voltage is applied to a series LCR circuit. Derive expression for the average power dissipated over a cycle.
Under What condition (i) no power is dissipated even though the current flows through the circuit?
(ii) Maximum power is dissipated in the circuit?
Video Solution
Text Solution
Voltage is applied to a series LCR circuit.
Current is
Instantaneous power supplied by the source is
The average power over a cycle is average of the two terms on the R.H.S of the above equation. The second term is time dependent, so, its average is zero.
is called the power factor.
Case I : For pure inductive circuit or pure capacitive circuit, the phase difference between current and voltage is
Therefore no power is dissipated. This current is sometimes referred to as wattless current.
Case II : For power dissipated at resonance in an LCR circuit,
" "therefore Cosphi=1
So, maximum power is dissipated.
|
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET-II
35 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET-III
25 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET III
9 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
A voltage V=Vmsinωt is applied to a series L-C-R circuit. Derive the expression for the average power dissipated over a cycle. Under what condition (i) no power is dissipated even though the current flows through the circuit, (ii) maximum power is dissipated in the circuit ?
View SolutionThe power dissipated in the following circuit is
View Solution
Knowledge Check
When a voltage V=V0 cos ωt is applied across a resistor of resistance R, the average power dissipated per cycle in the resistor is given by
AV0√2RBV0√2ωRCV202RDV202ωRIn the series LCR circuit, the power dissipation is through
ARBLCCDBoth L and CThe average power dissipated in an AC circuit containing a resistance along is
AermsIrmsBermsIrmscosϕC0Dnone of these
The power dissipated in the adjacent circuit is -
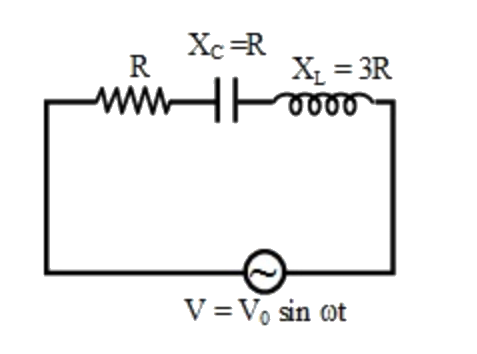
View SolutionDerive the expression for the power dissipated by an ideal resistor in an AC circuit .
View SolutionThe average power in LCR series circuit is
View SolutionThe average power dissipation in a pure capacitance in AC circuit is
View SolutionIf the current through a resistor in a circuit increases by 3%, the power dissipated by the resistor
View Solution
