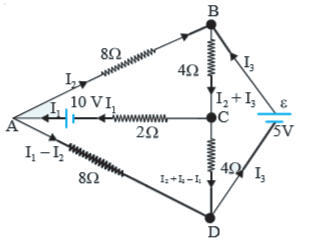
Determine current in each branch of the network shown in figure 

In the closed circuit ABCA,
(I1−I34+(I1+I2−I3)2+I1×1=10
or 7I1+2I2−6I3=10
In the closed circuit ADCA,
I3×4+(I3−I2)2+I1×1=10
or I1−2I2+6I3=10
In the closed current ABEDA
(I1−I3)4−I3×4=−5
or 4I1−8I3=−5
On solving (i), (ii) and (iii), we get
I1=2.5A
I2=1.875A=I3
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Conceptual Problems
3 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Very short Q/A
7 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
Similar Questions
Determine the current in each branch of the network shown in figure.
View Solution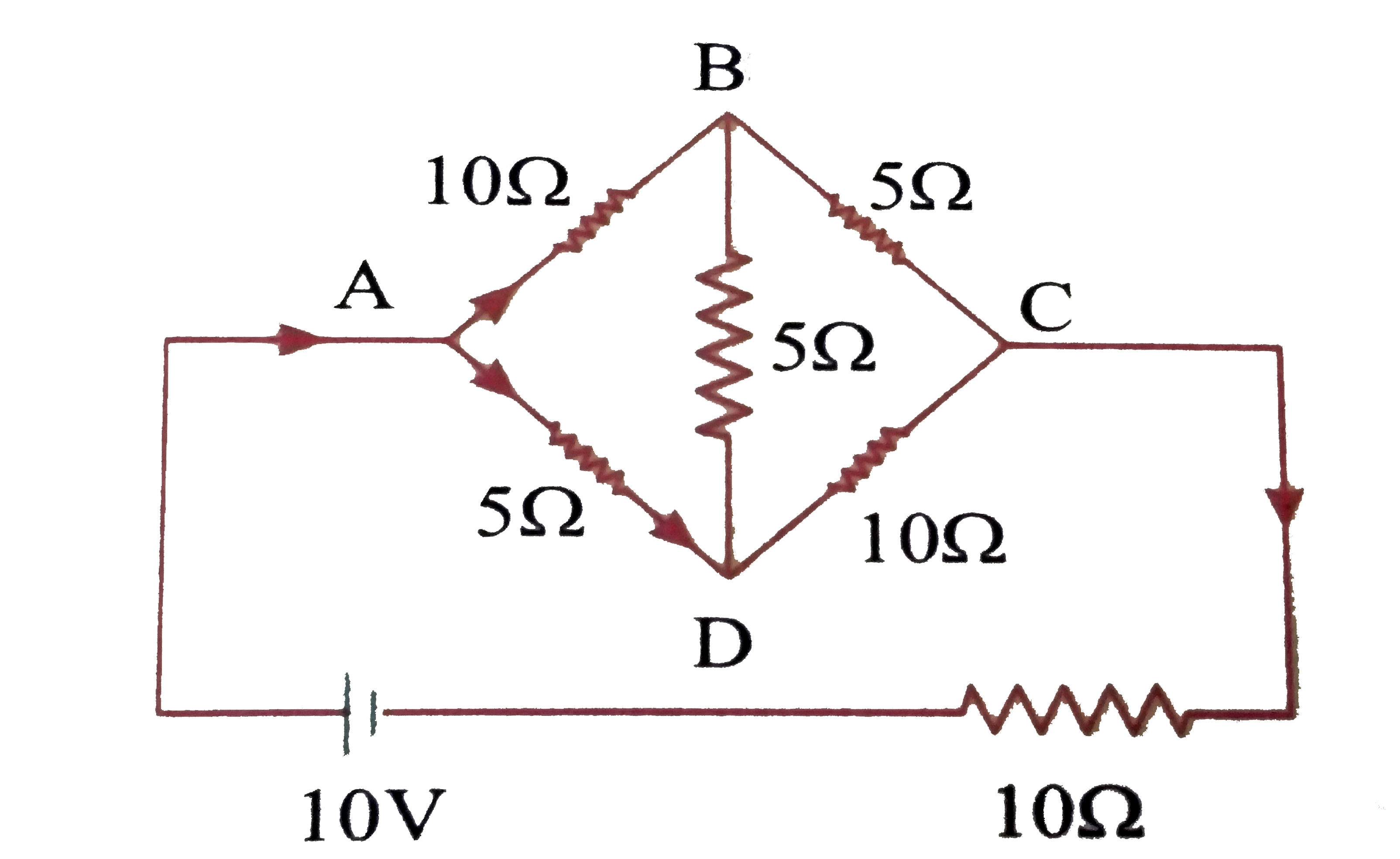
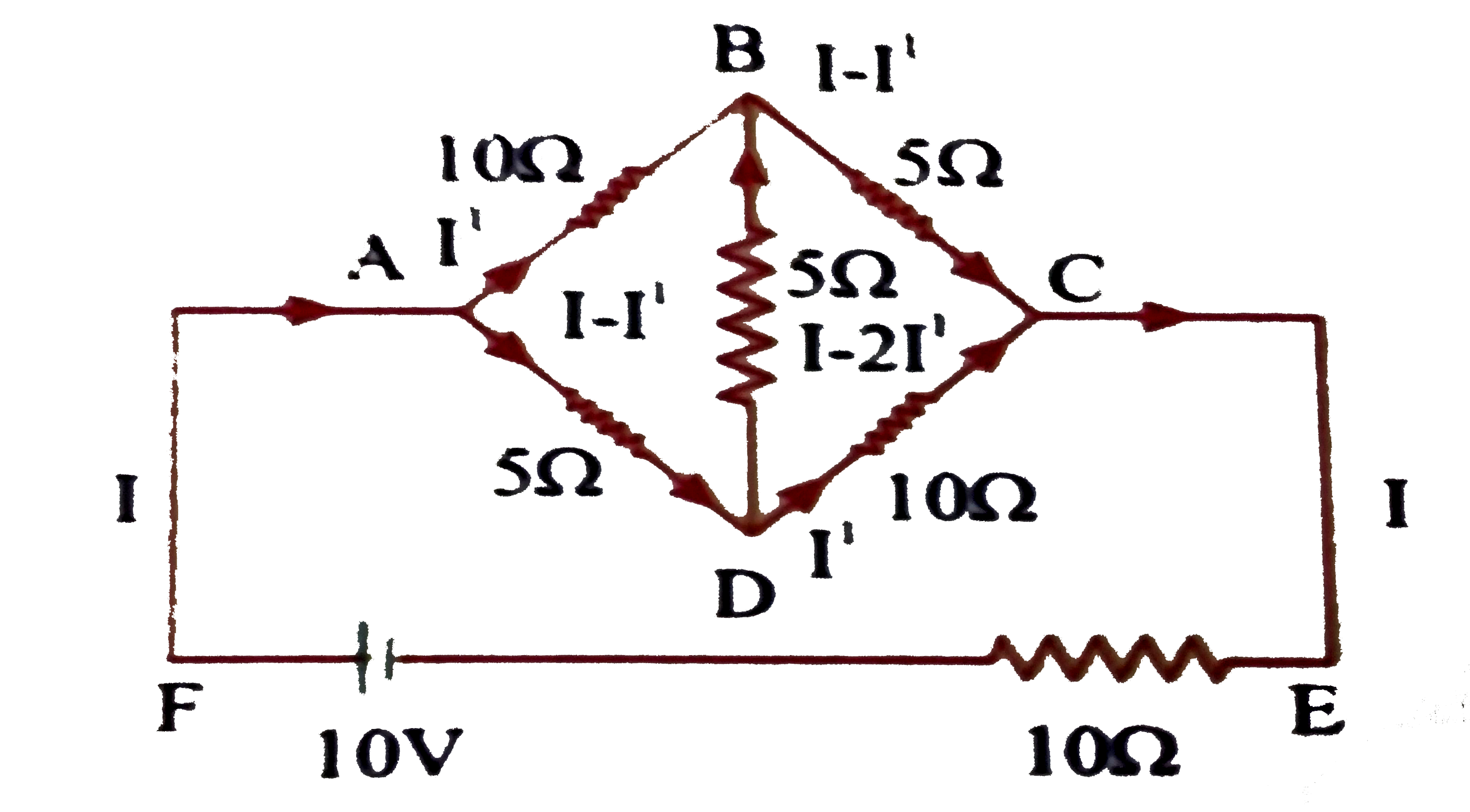
Determine the current in each branch of the network shown in fig.
View SolutionDetermine the current in each branch of the network shown in Fig.
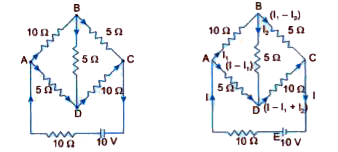
View SolutionDetermine the current in each branch of the network shown in Fig. 3.24

View SolutionFind the current in each branch of the cirucit shown in figure
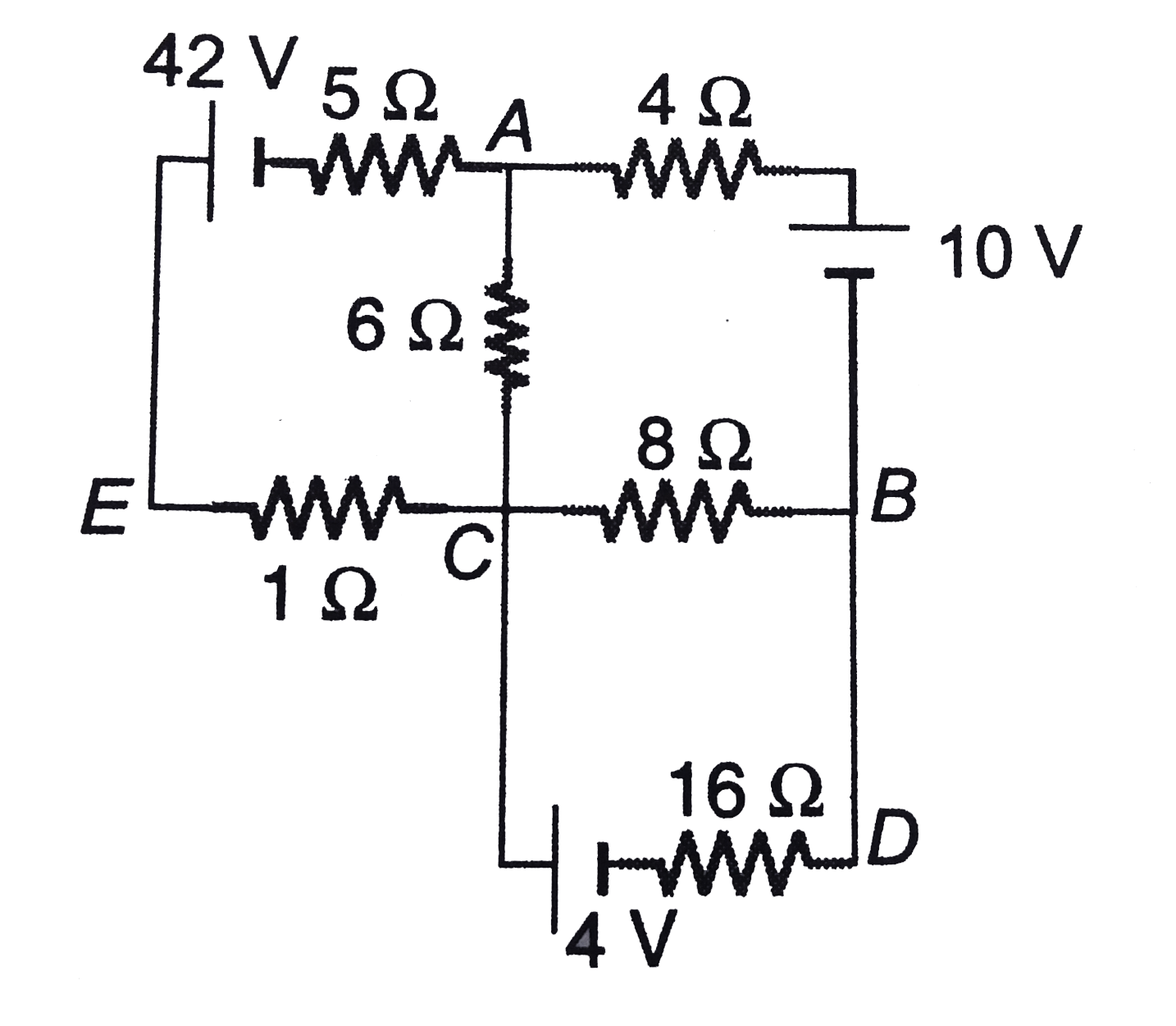
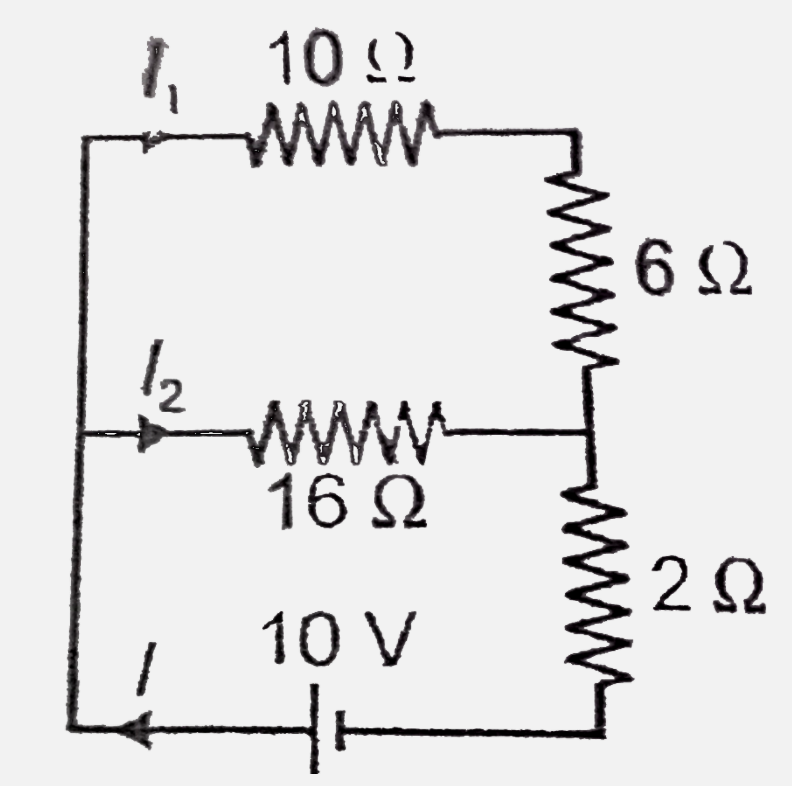
View SolutionCurrent l in the network shown in figure is
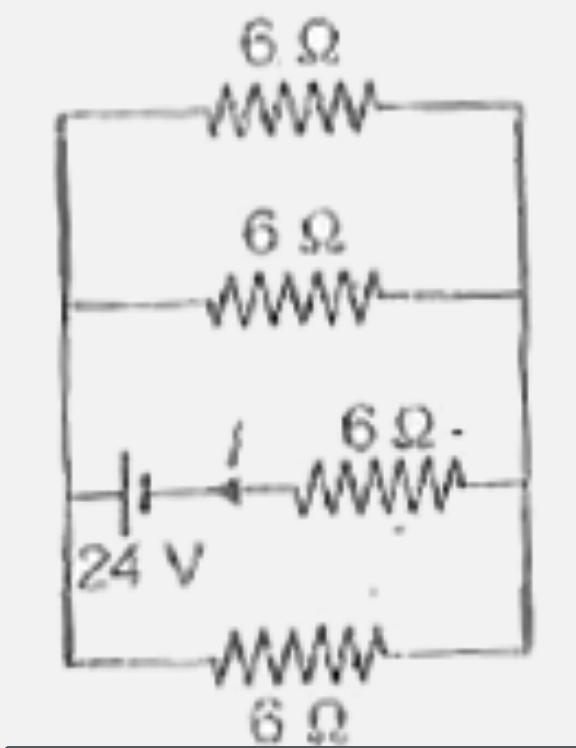
View SolutionCurrent l in the network shown is figure is
View Solution
calculate the current flowing in each of the resistances of the network shown in figure. The internal resistance of each cell is negligible.
View SolutionCalculate battery current and equivalent resistance of the network shown in figure.
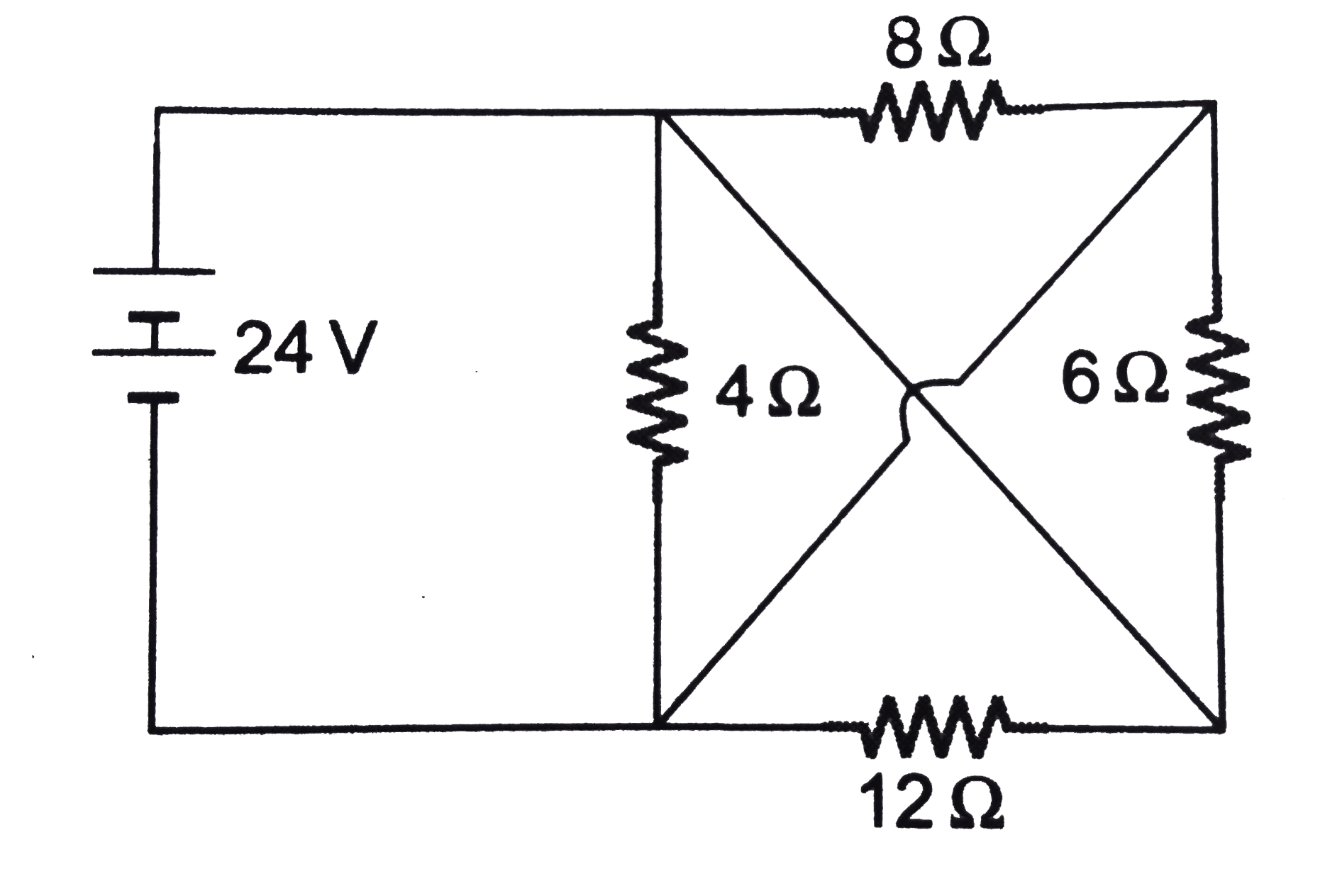
View SolutionFind the equivalent resistances between the points a and c of the network shown in figure. Each resistance is equal to r.
View Solution
