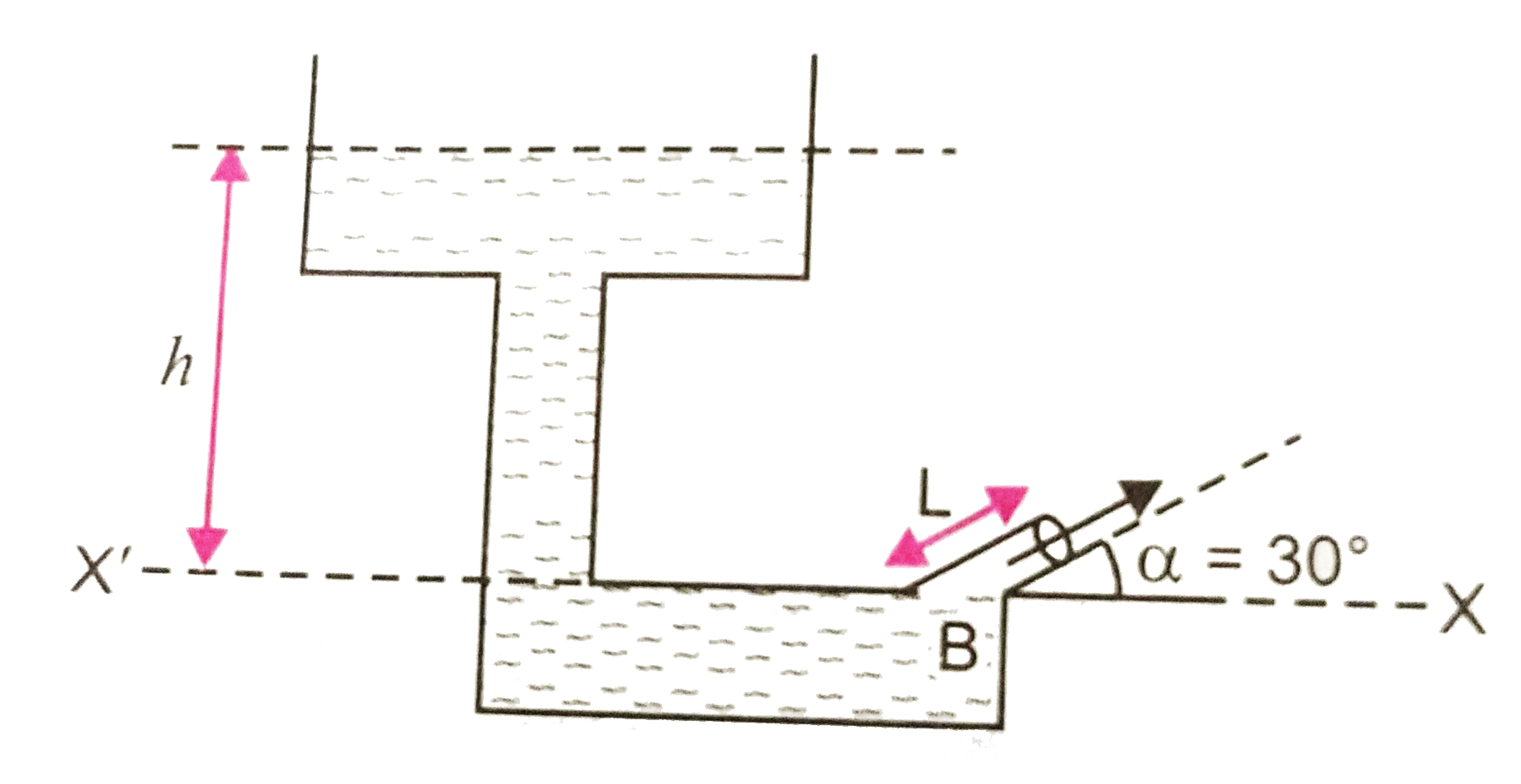
Determine the hight above the dashed line XX' attained by the water stream coming out through the hole is situtade at point B in the diagram given below. Given that h=10m,L=2m and α=30∘.
10 m
7.1 m
5 m
3.2 m
The correct Answer is:D
Let vB be the velocity of water coming out from the hole at B. Vertical height of tube of length L at B =Lsinα From law of conservation of total mechanical energy, we have
mg(h−Lsinα)=12mv2B
or v2B=2g(h−Lsinα)
=2g[10−2×1/2]=18g
Let H be the maximum height attained by stream of water coming out of hole, then
H=Lsinα+v2Bsin2α2g
=2×1/2+18g×(1/2)22g=1+94=3.25m
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Integer Type Questions
12 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Asseration - Reason Type Question
18 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions-II
14 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
Find the slope of the lines passing through the given points
L(−2,−3)andM(−6,−8)
View SolutionShows a large closed cylindrical tank containing water, Initially the air trapped above the water surface has a height h0and pressure2p0where p0is the atmospheric pressure. There is a hole in the wall of tank at a depth h1below the top from which water comes out. A long vertical tube is connected as shown. (a) Find the height h2 of the water in the long tube above the top initially. (b) Find the speed with which water comes out of hole.(c)Find the height of the water in the long tube above the top when the water stops coming out of the hole.

View Solution
Knowledge Check
A person in a lift is holding a water jar, which has a small hole at the lower end of its side. When the lift is at rest, the water jet coming out of the hole hits the floor of the lift at a distance d of 1.2 m from the person. In the following, state of the lift's motion is given in List I and the distance where the water jet hits the floor of the lift is given in List II. Match the statements from List I with those in List II and select the correct answer using the code given below the lists.
 APQRS2324BPQRS2314CPQRS1114DPQRS2311
APQRS2324BPQRS2314CPQRS1114DPQRS2311Consider the line ←→PQ given below and find whether the given statements are true or false
L , M and N are points on line segment ¯¯¯¯¯¯LN.
 ATrueBFalseCCannot be determinedDNone of the above
ATrueBFalseCCannot be determinedDNone of the aboveA block of mass M and cylindrical tank which contains water having small hole at bottom, which is closed initially (total mass of cylinder + water is also M), are attached at two ends of an ideal string which passes over an ideal pulley as shown. At t=0 hole is opened such that water starts coming out of the hole with a constant rate μkg/s and constant velocity Ve relative to the cyliender. aSccleration of the block at any time t will be : (Given that string always remains taut.)
 Aμ(Ve+gt)(2M−μt)BμVe(2M−μt)Cμgt(2M−μt)D2μVe(2M−μt)
Aμ(Ve+gt)(2M−μt)BμVe(2M−μt)Cμgt(2M−μt)D2μVe(2M−μt)
Water leaks out from an open tank through a hole of area 2mm2 in the bottom. Suppose water is filled up to a height of 80 cm and the area of cross section of the tankis 0.4m2. The pressure at the open surface and the hole are equal to the atmospheric pressure. Neglect the small velocity of the water near the open surface in the tank. a. Find the initial speed of water coming out of the hole. b. Findteh speed of water coming out when half of water has leaked out. c. Find the volume of water leaked out during a time interval dt after the height remained is h. Thus find the decrease in height dh in term of h and dt.
d. From the result of part c. find the time required for half of the water to leak out.
View SolutionThe U-tube acts as a water siphon. The bend in the tube is 1m above the water surface. The tube outlet is 7m below the water surface. The water issues from the bottom of the siphon as a free jet at atmospheric pressure. Determine the speed of the free jet and the minimum absolute pressure of the water in the bend. Given atmospheric pressure =1.01×105N/m2,g=9.8m/s2 and density of water =103kg/m3
 .
.
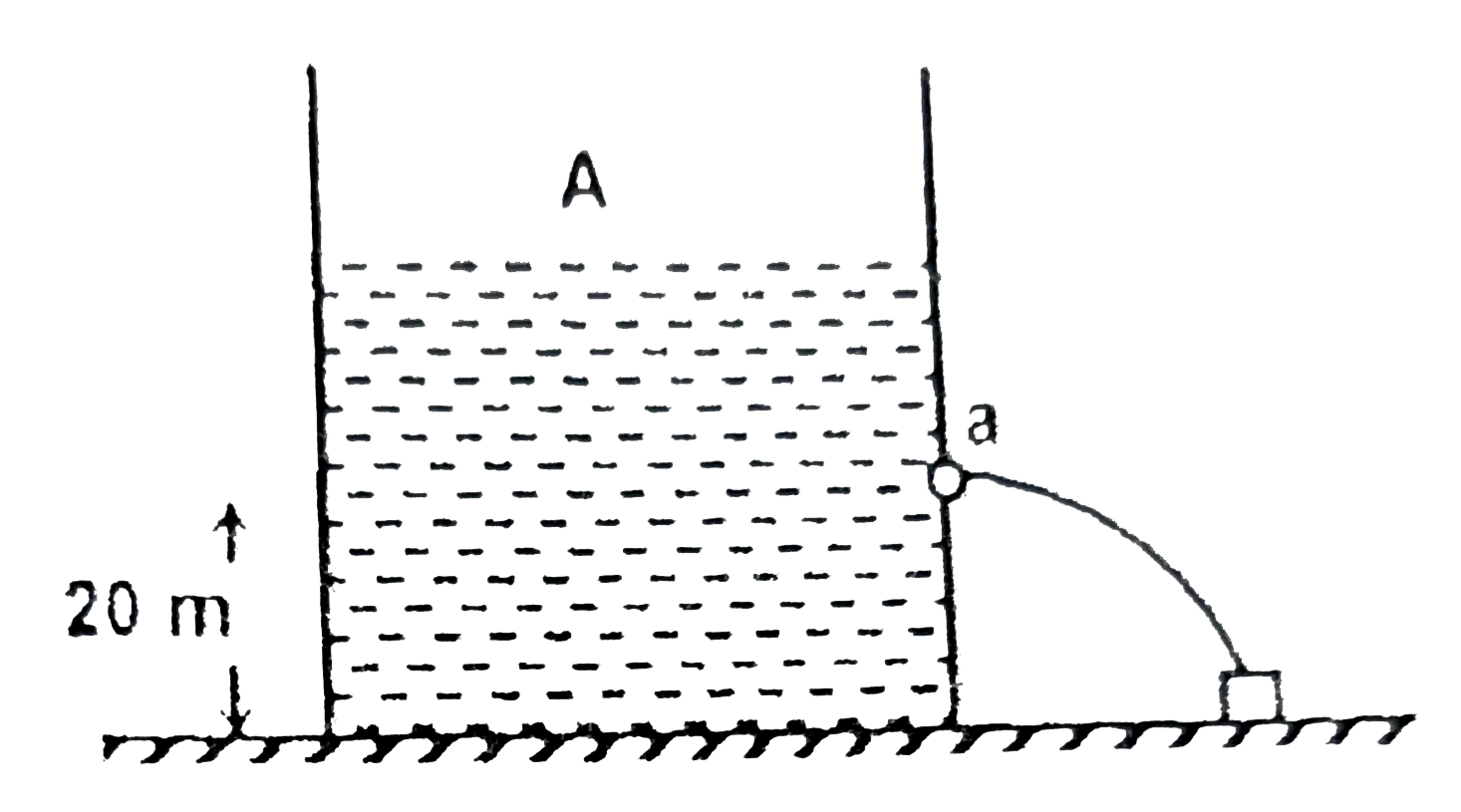
View SolutionWater is filled in a uniform container of area of cross section A. A hole of cross section area a (<<A) is made in the container at a height of 20m above the base. Water streams out and hits a small block on surface at some distance from container. Block is moved on surface in such a way that stream always hits the block. The initial velocity of the block (in m/s) is (Given aA=120). (Take g=10ms−2)
View SolutionThe range of water flowing out of a small hole made at a depth 10m below water surface in a large tank is R. Find the extra pressure (in atm) applied on the water surface so that range becomes 2R. Take 1atm=105Pa.

View SolutionA large tank is filled waith water (density =103kg/m3). A small hole is made at a depth 10 m below water surface. The range of water issuing out of the hole is R on ground. Approximately what extra pressure must be applied on the water surface so that the range becomes 2R
(take 1atm=105Pa and g=10m/s2)

View Solution
