Determine the minimum coefficient of friction μmin between a thin homogeneous rod and a floor at which a person can slowly lift the rod from the floor without slippage to the vertical position, applying to its end a force perpendicualr to it.
Step by step video & image solution for Determine the minimum coefficient of friction mu_(min) between a thin homogeneous rod and a floor at which a person can slowly lift the rod from the floor without slippage to the vertical position, applying to its end a force perpendicualr to it. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Determine the minimum coefficient of friction between a thin rod and a floor at which a person can slowly lift the rod from the floor, without slipping, to the vertical position applying at its end a force always perpendicular to its length.
View SolutionA block of mass m slips on a rough horizontal table under the action of horiozontal force applied to it. The coefficient of friction between the block and the table is μ. The table does not move on the floor. Find the total frictional force aplied by the floor on the legs of the table. Do you need the friction coefficient between the table and the floor or the mass of the table ?
View Solution
Knowledge Check
A body of mass M is applying horizontal force to slide a box of mass M1 on a rough horizontal surface The coefficient of friction between the shoe of the boy and the floor is μ and that between the box and the floor is 'μ1' In which of the following cases is it certainly not possible to slide the box ? .
Aμ<μ1,M<M1Bμ>μ1,M>M1Cμ<μ1,M>M1Dμ1>μ1,M<M1A body of mass M is applying horizontal force to slide a box of mass M1 on a rough horizontal surface The coefficient of friction between the shoe of the boy and the floor is μ and that between the box and the floor is 'μ1' In which of the following cases is it certainly not possible to slide the box ? .
Aμ<μ,M<M'Bμ>μ',M<M'Cμ<μ',M>M'Dμ>μ'M>M'A boy of mass M is applying a horizontal force to slide a box of mass M1 on rough horizontal surface. The coefficient of friction between the shoe of the boy and the floor is μ and that between the box and the floor is ‘μ1’ In which of the following cases is it certainly not possible to slide the box ?
Aμ<μ1,M<M1Bμ>μ3,M>M1Cμ<μ1,M>M1Dμ>μ1,M<M1
The friction coefficient between the board and the floor shown in figure is μ Find the maximum force that the man can exert on the rope so that the board does not slip on the floor

View SolutionA uniform rod is made to lean between a rough vertical wall and the ground. The coefficient of friction between the rod and the ground is μ1 and between the rod and the wall is μ2. Find the angle at which the rod can he leaned without slipping.
View SolutionA uniform beam of mass m is inclined at an angle θ to the horizontal. Its upper end produces a ninety degree bend in a very rough rope tied to a wall, and its lower end rests on a rough floor (a) If the coefficient of static friction between beam and floor is μs determine an expression for the maximum mass M that can be suspended from the top before the beam slips. (b) Determine the magnitude of the reaction force at the floor and the magnitude of the force exerted by the beam on the rope at P in terms of m,M and μs
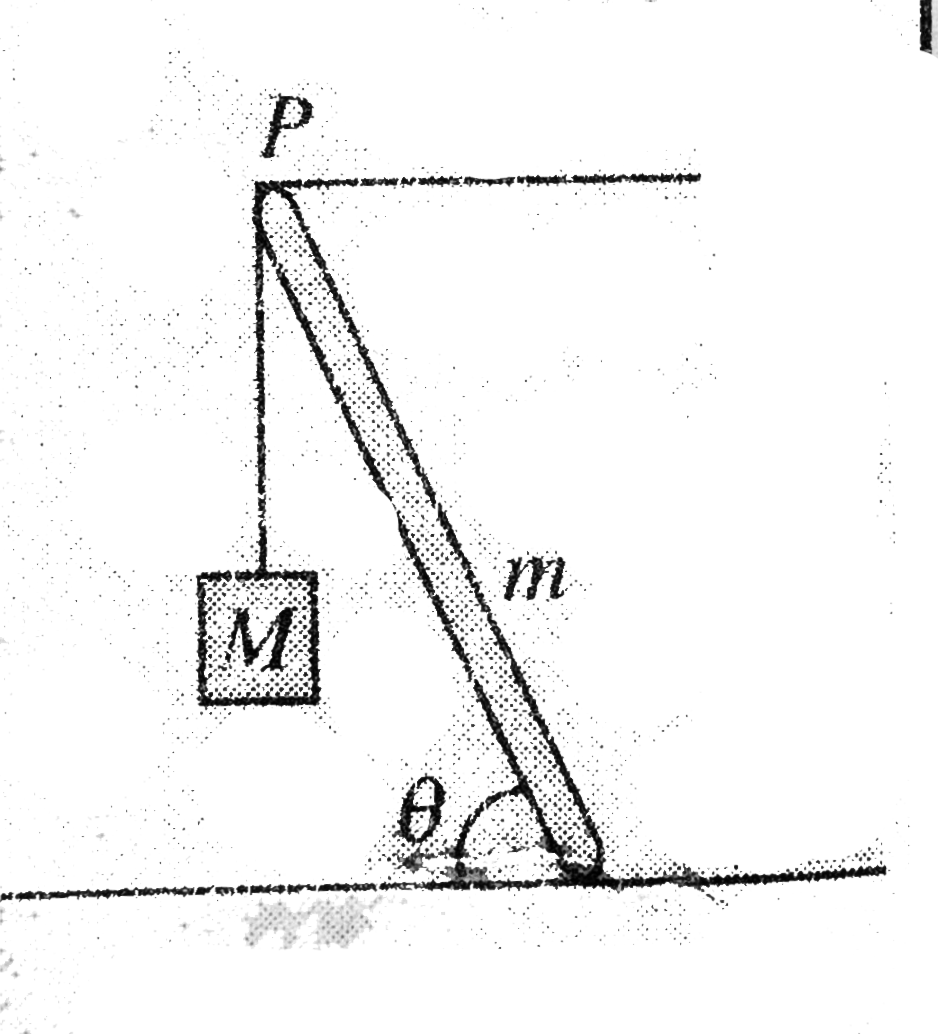 .
.
View SolutionA uniform rod ABC of mass M is placed vertically on a rough horizontal surface. The coefficient of kinetic friction between the rod and the surface is μ.A force F (>μmg) is applied on the rod at point B at distance l/3 below centre of the rod as shown in figure. The initial acceleration of point A is
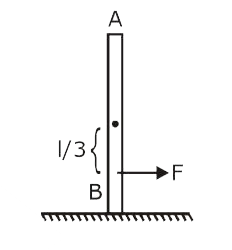
View SolutionA horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.
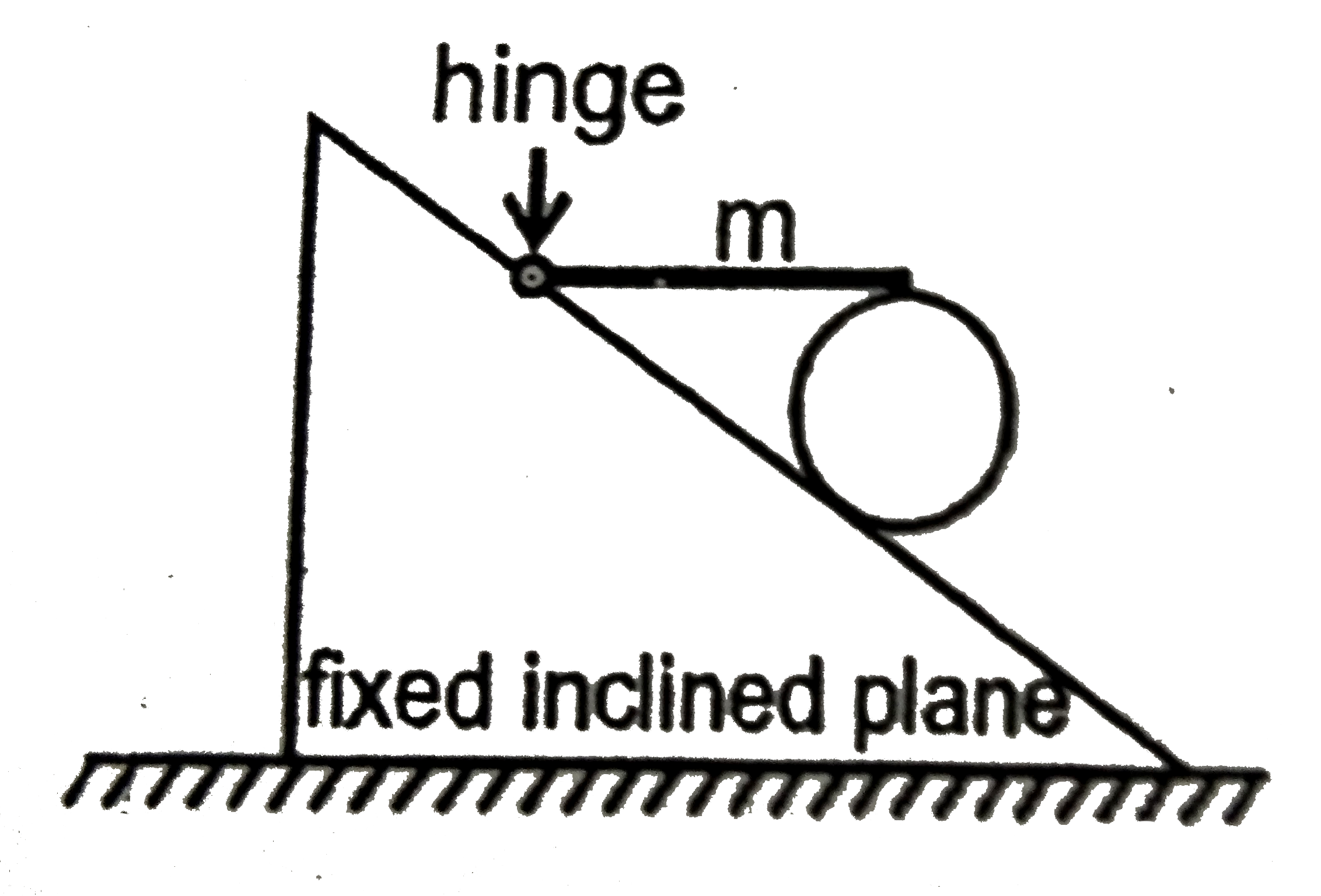
The ratio of magnitude of frictional force on the cylinder due to the rod and the magnitude of frictional force on the cylinder due to the inclined plane is :
View Solution
