Diameter of a planet is 10d∘, its mean density is ρ∘4 and mass of its atmosphere is 10m∘ where d∘, ρ∘ and m∘ are diameter, mean density and mass of atmosphere respectively for the earth. Assume that mean density of atmosphere is same on the planet and the earth and height of atmosphere on both the planets is very small compared to their radius. Find the ratio of atmospheric pressure on the surface of the planet to that on the earth. If a mercury barometer reads 76 cm on the surface of the earth, find its reading on the surface of the planet.
The correct Answer is:(a) 52
(b) 7.6cm
Step by step video, text & image solution for Diameter of a planet is 10d_(@), its mean density is (rho_(@))/(4) and mass of its atmosphere is 10m_(@) where d^(@), rho^(@) and m^(@) are diameter, mean density and mass of atmosphere respectively for the earth. Assume that mean density of atmosphere is same on the planet and the earth and height of atmosphere on both the planets is very small compared to their radius. Find the ratio of atmospheric pressure on the surface of the planet to that on the earth. If a mercury barometer reads 76 cm on the surface of the earth, find its reading on the surface of the planet. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
We know that the atmospheric pressure on the surface of the earth is because of weight, of the air. The radius of the earth is 6400 km and atmospheric pressure on the sruface of earth is 1×105N/m2. Estimate the mass of the earth's atmosphere assuming that acceleration due to gravity remains constant at 10m/s2 over the entrie height of the atmospehre.
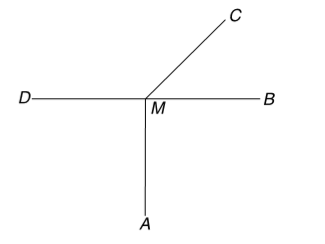
View SolutionFour metal rods each of length L and cross sectional area A are joined at point M. Thermal conductivities of MA, MB and MD are equal and that of MC is thrice that of MA. The end points A, B, C and D are kept in large reservoirs. Heat folws into the junction from B at a rate of P(Js−1) and C from at a rate of 3P. Heat flows out of D at a rate of 5P.
(a) Find the relation between temperatures of points A, B and C.
(b) Find temperature of D if temperature of A and M and TA and TM respectively.
View SolutionSuppose that the acceleration of a free fall at the surface of a distant planet was found to be equal to that at the surface of the earth. If the diameter of the planet were twice the diameter of the earth, then the ratio of mean density of the planet to that of the earth would be
View SolutionIf the density of a small planet is the same as that of earth while the radius of the planet is 0.2 times that of the earth the gravitational on the surface of that planet is :
View SolutionA planet is a homogeneous ball of radius R having mass M. It is surrounded by a dense atmosphere having density ρ=σ∘r where simga∘ is a constant and r is distance from the centre of the planet. It is found that acceleration due to gravity is constant throughout the atmosphere of the planet. Find simga∘in terms of M and R.
View SolutionAtmosphere of a planet contains only an ideal gas of molar mass M0. The temperature of the atmosphere varies with height such that the density of atmosphere remains same throughout. The planet is a uniform sphere of mass M and radius ‘a’. Thickness of atmosphere is small compared to ‘a’ so that acceleration due to gravity can be assumed to be uniform throughout the atmosphere.
(a) Find the temperature difference between the surface of the planet and a point at height H in its atmosphere
(b) If the rms speed of gas molecules near the surface of the planet is half the escape speed, calculate the temperature of the atmosphere at a height H above the surface. Assume CpCV=γ for the atmospheric gas
View SolutionThe diameter of a planet is four times that of the earth. Find the time period of pendulum on the planet, if it is a second pendulum on the earth. Take the mean density of the planet equal to the earth,
View SolutionThe diameters of two planets are in the ratio 4 : 1 and their mean densities in the ratio 1 : 2. The acceleration due to gravity on the planets will be in ratio
View SolutionA planet has twice the radius but the mean density is 14 th as compared to earth. What is the ratio of escape velocity from earth to that from the planet
View SolutionThe diameter of a planet is four times that of the earth. Find the time period of a pendulum on the planet, if it is a second pendulum on the earth. Take the mean density of the planet equal to that of the earth,
View Solutionपृथ्वी तल पर पलायन चाल ve है । एक ग्रह की त्रिज्या पृथ्वी की त्रिज्या से 4 गुनी है । ग्रह के तल पर पलायन चाल क्या होगा यदि - (i) ग्रह का द्रव्यमान पृथ्वी के द्रव्यमान के बराबर है (ii) ग्रह का घनत्व पृथ्वी के घनत्व के बराबर है ?
View SolutionThe ratio of the weight of a body on the Earth’s surface to that on the surface of a planet is 9 : 4. The mass of the planet is 19 of that of the Earth. If ‘R’ is the radius of the Earth, then the radius of the planet is where n is ___________ . (Take the planets to have the same mass density)
View SolutionA planet of mass M and radius a is surrounding by an atmosphere of constant density consisting of a gas of molar mass mu . Find the temperature T of the atmosphere on the surface of the planet if the height of the atmosphere is h lt lt a.
View SolutionThe diameter and density of a planet are twice that of the earth. Assuming the earth and the planet to be of uniform density, find the ratio of the lengths of two simple pendulums, of equal time periods, on the surface of the planet and the earth.
View SolutionIf the density of small planet is that of the same as that of the earth while the radius of the planet is 0.2 times that of the Earth, the gravitational acceleration on the surface for the planet is........
View Solution
