Displacement-time equation of a particle moving along x-axis is x=20+t3−12t (SI units)
(a) Find, position and velocity of particle at time t=0.
(b) State whether the motion is uniformly accelerated or not.
(c) Find position of particle when velocity of particle is zero.
(i) Given, displacement-time equation of a particle P
x=20+t3−12t ….(i)
At t=0,x=20+0−0=20m
Velocity of particle at time t can be obtained by differentiating Eq. (i) w.r.t. time i.e.,
v=dxdt=3t2−12 ….(ii)
At t=0,v=0−12=−12m/s
(ii) Differentiating Eq. (ii) w.r.t. time t, we get the acceleration,
a=dvdt=6t
As acceleration is a function of time, the motion is non-uniformly accelerated.
(iii) Substituting v=0 in Eq. (ii), we have
0=3t2−12
Positive value of t comes out to be 2 s from this equation. Substituting t = 2 s in Eq. (i), we have,
x=20+(2)3−12(2) or x=4m
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.110videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.210videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery19videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
Similar Questions
Find the time t0 when x-coordinate of the particle is zero.
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View SolutionThe position of a particle moving along x-axis given by x=(−2t3−3t2+5)m. The acceleration of particle at the instant its velocity becomes zero is
View SolutionThe displacement x of a particle moving along x-axis at time t is given by x2=2t2+6t. The velocity at any time t is
View SolutionThe acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is −5m/s, the velocity at t = 8 s is
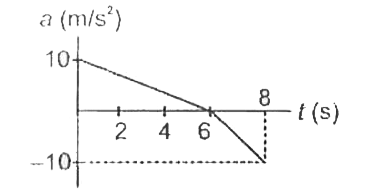 View Solution
View SolutionFigure shows the displacement-time graph of a particle moving in a straight line. Find the signs of velocity and acceleration of particle at time t=t1andt=t2.
 View Solution
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
 View Solution
View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.
 View Solution
View Solutionx-coordinate of a particle moving along this axis is x=(2+t2+2t3). Here, x is in meres and t in seconds. Find (a) position of particle from where it started its journey, (b) initial velocity of particle and (c) acceleration of particle at t=2s.
View SolutionThe position (x) of a particle moving along x - axis veries with time (t) as shown in figure. The average acceleration of particle in time interval t = 0 to t = 8 s is
 View Solution
View Solution
