Does it matter if one uses gauge instead of absolute pressures in applying Bernoulli's equation. Explain.
To determine whether it matters if one uses gauge pressure instead of absolute pressure when applying Bernoulli's equation, we can follow these steps:
Step 1: Understand the Definitions
- Gauge Pressure (Pg): This is the pressure measured relative to atmospheric pressure. It does not include the atmospheric pressure in its value.
- Absolute Pressure (Pa): This is the total pressure measured relative to a perfect vacuum. It includes atmospheric pressure.
Step 2: Relationship Between Gauge and Absolute Pressure
- The relationship between gauge pressure and absolute pressure can be expressed as:
Pa=Pg+Patm
where Patm is the atmospheric pressure.
Step 3: Write Bernoulli's Equation
- Bernoulli's equation states:
P+12ρV2+ρgh=constant
where P is the pressure at a point, ρ is the fluid density, V is the fluid velocity, and h is the height above a reference level.
Step 4: Apply Bernoulli's Equation Between Two Points
- When applying Bernoulli's equation between two points (1 and 2), we can write:
P1+12ρV21+ρgh1=P2+12ρV22+ρgh2
Step 5: Substitute Absolute Pressure with Gauge Pressure
- If we substitute absolute pressures P1 and P2 with gauge pressures, we have:
(Pg1+Patm)+12ρV21+ρgh1=(Pg2+Patm)+12ρV22+ρgh2
Step 6: Simplify the Equation
- Rearranging gives:
Pg1+Patm+12ρV21+ρgh1=Pg2+Patm+12ρV22+ρgh2
- Notice that Patm appears on both sides of the equation and can be canceled out:
Pg1+12ρV21+ρgh1=Pg2+12ρV22+ρgh2
Step 7: Conclusion
- Since the atmospheric pressure cancels out, it shows that using gauge pressure instead of absolute pressure does not affect the application of Bernoulli's equation. Therefore, it does not matter whether gauge or absolute pressure is used in this context.
- Gauge Pressure (Pg): This is the pressure measured relative to atmospheric pressure. It does not include the atmospheric pressure in its value.
- Absolute Pressure (Pa): This is the total pressure measured relative to a perfect vacuum. It includes atmospheric pressure.
- The relationship between gauge pressure and absolute pressure can be expressed as:
Pa=Pg+Patm
where Patm is the atmospheric pressure.
- Bernoulli's equation states:
P+12ρV2+ρgh=constant
where P is the pressure at a point, ρ is the fluid density, V is the fluid velocity, and h is the height above a reference level.
- When applying Bernoulli's equation between two points (1 and 2), we can write:
P1+12ρV21+ρgh1=P2+12ρV22+ρgh2
- If we substitute absolute pressures P1 and P2 with gauge pressures, we have:
(Pg1+Patm)+12ρV21+ρgh1=(Pg2+Patm)+12ρV22+ρgh2
- Rearranging gives:
Pg1+Patm+12ρV21+ρgh1=Pg2+Patm+12ρV22+ρgh2
- Notice that Patm appears on both sides of the equation and can be canceled out:
Pg1+12ρV21+ρgh1=Pg2+12ρV22+ρgh2
- Since the atmospheric pressure cancels out, it shows that using gauge pressure instead of absolute pressure does not affect the application of Bernoulli's equation. Therefore, it does not matter whether gauge or absolute pressure is used in this context.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Higher Order thinking skells17videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Value Based Question5videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Advanced problems for competitions21videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
Bernoulli's principle does not explain :
Acurved path of a spinning ball.Blift of a jet.Cworking of a point sprayer.Dautomatic blowing of 7 the roots of houses during lizard in hilly areas. - Question 2 - Select One
Statement-1 : Bernoullis equation is based on energy conservation.
Statement-2 : Bernoullis equation can only be applied if the flow is streamlined.
Statement-3 : Bernoullies equation can be applied evern if the flow is not streamlined as total energy is always conserved.AT T TBT F TCT T FDF F F - Question 3 - Select One
using the illustration when both surfaces 1 and 2 are exposed to the atmoshere, P1 and P2 are gauge pressure , and h1 and h2 are heights .
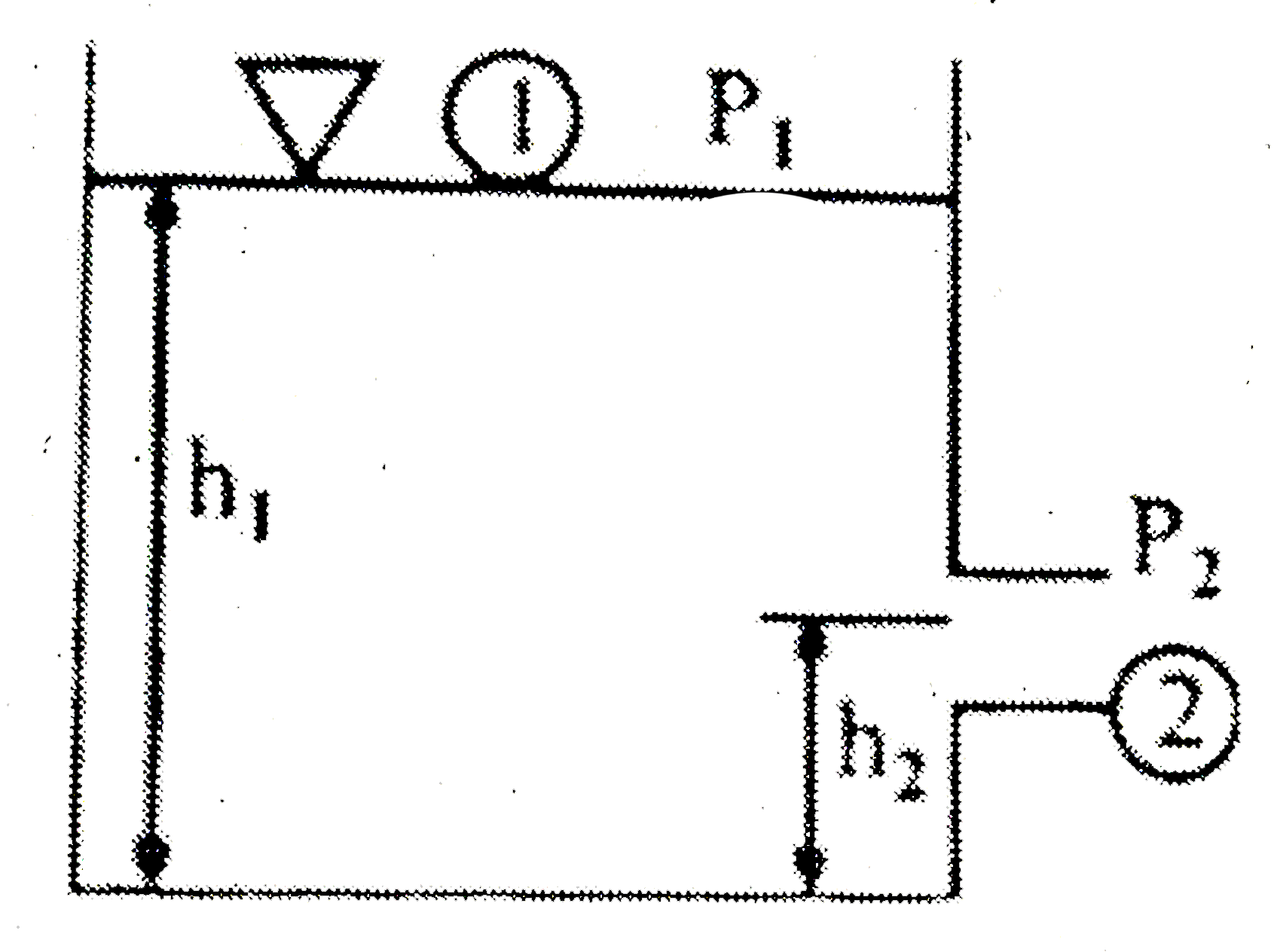
The Bernoulli equation for this situation is h1+P1W+V212a=h2+P2W+V222a
The velocity of the fluid leavening point (2) is constant and can be expressed asAV2=(P1/P2)V1BV2=(P1/P2)ahCV2=[(h1−h2)(2a)]1/2Dnone of the above
Problems based on Pressure Variation | Archimedes Principle and Bernoulli's Equation
View SolutionDesalination of seawater is done by using reverse osmosis. The pressure applied to the solution is
View SolutionAbsolute Pressure And Gauge Pressure
View SolutionExplain about the instruments used to measure atmospheric pressure.
View Solutionusing the illustration when both surfaces 1 and 2 are exposed to the atmoshere, P1 and P2 are gauge pressure , and h1 and h2 are heights .

The Bernoulli equation for this situation is h1+P1W+V212a=h2+P2W+V222a
The value of P1 and P2 are such thatView Solution

