Draw distance time graph of a body (i) at rest
(ii) in uniform motion and
(iii) in non uniform motion.
To solve the question of drawing distance-time graphs for a body at rest, in uniform motion, and in non-uniform motion, we will follow these steps:
Step 1: Distance-Time Graph for a Body at Rest
1. Understanding the Condition: When a body is at rest, it does not change its position over time. This means that the distance remains constant.
2. Graph Representation: On a graph where the x-axis represents time and the y-axis represents distance, the graph will be a horizontal line.
- Coordinates: For example, if the body is at a distance of 0 meters, the graph will be a horizontal line along the y-axis at 0 meters for all values of time.
Step 2: Distance-Time Graph for a Body in Uniform Motion
1. Understanding the Condition: In uniform motion, the body moves at a constant speed. This means that for equal intervals of time, the distance covered is the same.
2. Graph Representation: The graph will be a straight line with a constant slope.
- Slope Interpretation: The slope of the line represents the speed of the body. If the body moves 10 meters in 2 seconds, the slope will be 5 meters/second.
- Coordinates: For example, if the body moves from 0 meters to 10 meters in 2 seconds, the line will rise steadily from (0,0) to (2,10).
Step 3: Distance-Time Graph for a Body in Non-Uniform Motion
1. Understanding the Condition: In non-uniform motion, the body’s speed changes over time. This means that the distance covered in equal intervals of time is not the same.
2. Graph Representation: The graph will be a curve, typically a parabolic shape, indicating that the velocity is changing.
- Slope Interpretation: The slope of the curve changes at different points, indicating varying speeds. For instance, the body may accelerate at first and then decelerate.
- Coordinates: For example, the graph may start at (0,0), rise steeply at first, and then level off, showing that the body is speeding up and then slowing down.
Summary of Graphs
- At Rest: Horizontal line (e.g., y = 0).
- Uniform Motion: Straight line with constant slope (e.g., y = mx + c).
- Non-Uniform Motion: Curved line (e.g., a parabolic curve).
1. Understanding the Condition: When a body is at rest, it does not change its position over time. This means that the distance remains constant.
2. Graph Representation: On a graph where the x-axis represents time and the y-axis represents distance, the graph will be a horizontal line.
- Coordinates: For example, if the body is at a distance of 0 meters, the graph will be a horizontal line along the y-axis at 0 meters for all values of time.
1. Understanding the Condition: In uniform motion, the body moves at a constant speed. This means that for equal intervals of time, the distance covered is the same.
2. Graph Representation: The graph will be a straight line with a constant slope.
- Slope Interpretation: The slope of the line represents the speed of the body. If the body moves 10 meters in 2 seconds, the slope will be 5 meters/second.
- Coordinates: For example, if the body moves from 0 meters to 10 meters in 2 seconds, the line will rise steadily from (0,0) to (2,10).
1. Understanding the Condition: In non-uniform motion, the body’s speed changes over time. This means that the distance covered in equal intervals of time is not the same.
2. Graph Representation: The graph will be a curve, typically a parabolic shape, indicating that the velocity is changing.
- Slope Interpretation: The slope of the curve changes at different points, indicating varying speeds. For instance, the body may accelerate at first and then decelerate.
- Coordinates: For example, the graph may start at (0,0), rise steeply at first, and then level off, showing that the body is speeding up and then slowing down.
- At Rest: Horizontal line (e.g., y = 0).
- Uniform Motion: Straight line with constant slope (e.g., y = mx + c).
- Non-Uniform Motion: Curved line (e.g., a parabolic curve).
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The velocity -time graph for a body with non-uniform motion is a
Astraight lineBstraight line parallel to x-axisCstraight line parallel to y-axisDcurved line - Question 2 - Select One
In a non- uniform circular motion
ATangential acceleration (at) is zeroBRadial acceleration (aR) is zeroCBoth (1) & (2) are correctDBoth at&aR are non zero - Question 3 - Select One
PASSAGE-I : A body is said to be in motion when its position changes continuously with respect to a stationary object taken as reference point. A body has a uniform motion if it travels equal distance in equal intervals of time, no matter how small these time intervals may be. The distance-time graph for uniform motion is a straight line. A body has a non-uniform motion if it travels unequal distance in equal intervals of time. The distance-time graph for a body having non-uniform motion is a curved line.
The distance-time graph for a uniform motion isA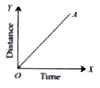 B
B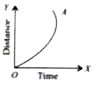 C
C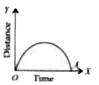 D
D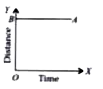
What is non-uniform motion ?
View SolutionHow is non-uniform motion different from uniform motion?
View SolutionExplain the terms : uniform motion and non-uniform motion with examples.
View SolutionUniform And Non Uniform Motion
View Solution(a) Draw distance time graph when a body is at rest. How is the graph modified when the body is moving with a uniform velocity ?
(b) A car moving at 36km/h is brought to rest in 0.1km. What is the retardation ?View Solution

