During blood transfusion the needle is inserted in a vein where gauge pressure is pg and atmospheric pressure is p. At what height must the blood container be placed so that blood may just enter the vein. Given density of blood is p.
To solve the problem of determining the height at which the blood container must be placed for blood to enter the vein during a transfusion, we can follow these steps:
1. Understand the Pressure Conditions:
- The gauge pressure in the vein is denoted as pg.
- The atmospheric pressure is denoted as p.
- The total pressure at the level of the vein must be equal to the pressure exerted by the blood column from the container.
2. Relate the Pressures:
- The pressure at the bottom of the blood container can be expressed as the sum of the atmospheric pressure and the gauge pressure:
Ptotal=p+pg
3. Use Hydrostatic Pressure Equation:
- The pressure due to a column of fluid (blood in this case) of height h is given by:
Pblood=ρgh
where ρ is the density of the blood, g is the acceleration due to gravity, and h is the height of the blood column.
4. Set the Pressures Equal:
- For the blood to just enter the vein, the pressure at the level of the vein must equal the pressure due to the blood column:
p+pg=ρgh
5. Solve for Height h:
- Rearranging the equation to solve for h:
h=p+pgρg
Final Expression:
The height h at which the blood container must be placed is given by:
h=p+pgρg
- The gauge pressure in the vein is denoted as pg.
- The atmospheric pressure is denoted as p.
- The total pressure at the level of the vein must be equal to the pressure exerted by the blood column from the container.
- The pressure at the bottom of the blood container can be expressed as the sum of the atmospheric pressure and the gauge pressure:
Ptotal=p+pg
- The pressure due to a column of fluid (blood in this case) of height h is given by:
Pblood=ρgh
where ρ is the density of the blood, g is the acceleration due to gravity, and h is the height of the blood column.
- For the blood to just enter the vein, the pressure at the level of the vein must equal the pressure due to the blood column:
p+pg=ρgh
- Rearranging the equation to solve for h:
h=p+pgρg
The height h at which the blood container must be placed is given by:
h=p+pgρg
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROPERTIES OF MATTEREXERCISE - Short Answer Type Questions (3 Marks)
24 Videos
- PROPERTIES OF MATTERBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROPERTIES OF MATTEREXERCISE - Long Answer Type Questions (5 Marks)
1 Videos
- PROPERTIES OF MATTERBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROPERTIES OF MATTEREXERCISE - MULTIPLE CHOICE QUESTIONS (MCQs)
20 Videos
- NEWTON'S LAWS OF MOTIONBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Laws Of Motion
20 Videos
- ROTATIONAL MOTION BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ROTATIONAL MOTION EXERCISE - MULTIPLE CHOICE QUESTIONS
20 Videos
Similar Questions
During blood transfusion the needle is inserted in a vein where the gauge pressure is 2000Pa . At what height must the blood container be placed so that blood may just enter the vein? Density of whole blood = 1.06×103Kg/m3.
View SolutionDuring blood transfusion the needle is inserted in a vein where the gauge pressure is 2000Pa . At what height must the blood container be placed so that blood may just enter the vein? Density of whole blood = 1.06×103Kg/m3.
View Solution
Knowledge Check
Figure shows a crude type of atomizer. is compressed, air flows swiftly through tube BC causing a reduced pressure in the particles of the vertical to Liquid rises in the tube, enters BC and is sprayed out. if the pressure in the bulb is Pa+P, where P is the gauge pressure and Pa is the atmospheric pressure, v is the speed of air in BC, find how large would v need to be to cause the liquid to rise to BC. Density of air =1.3kg/m3.
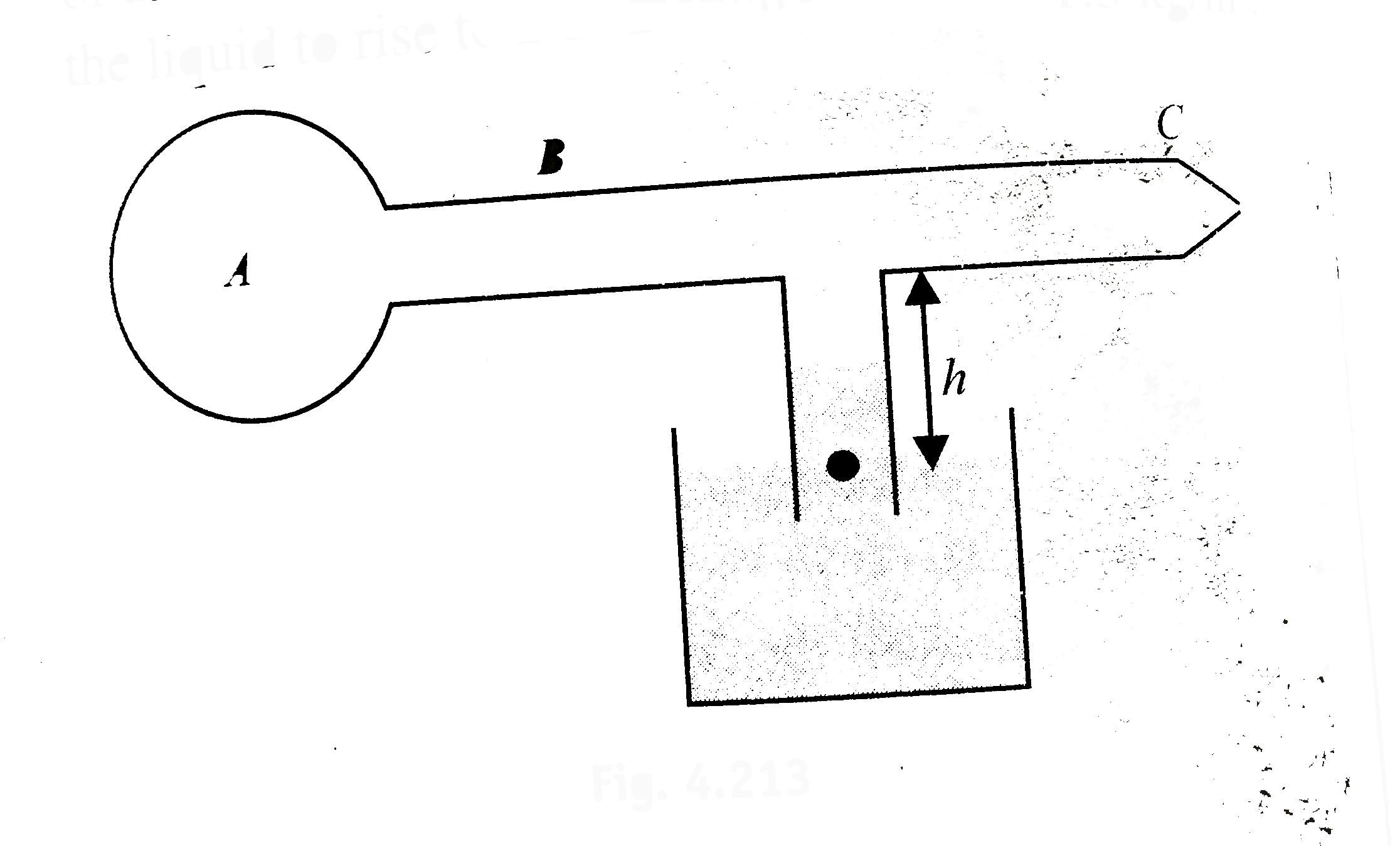 AP+ρgh√0.65BPhρg√0.650CP√hρg0.65DPhρg√0.65
AP+ρgh√0.65BPhρg√0.650CP√hρg0.65DPhρg√0.65Figure shows initial state of an ideal gas trapped in a container with conducting walls and a piston (mass m) which can move without any friction. The container is placed on point supports and its wall are conducting. Assuming that atmospheric pressure is P0 and the mass of the ideal gas is negligible as compared to the mass of the piston and the mass of container. Take the cross section area of piston to be A. The piston is slowly lifted by an external agent and held in its position. Let M be the maximum mass of container so that it may "lift off" while pulling the piston upwards and Pi be the pressure of ideal gas in initial state. Pick the correct choice:
 APi=P0+mgABPi=P02+mg2ACM=m2DM=P0A2g−m2
APi=P0+mgABPi=P02+mg2ACM=m2DM=P0A2g−m2A tube of uniform cross section is used to siphon water from a vessel V as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure (P0). The height of the tube above and below the water level in the vessel are h1 and h2, respectively.
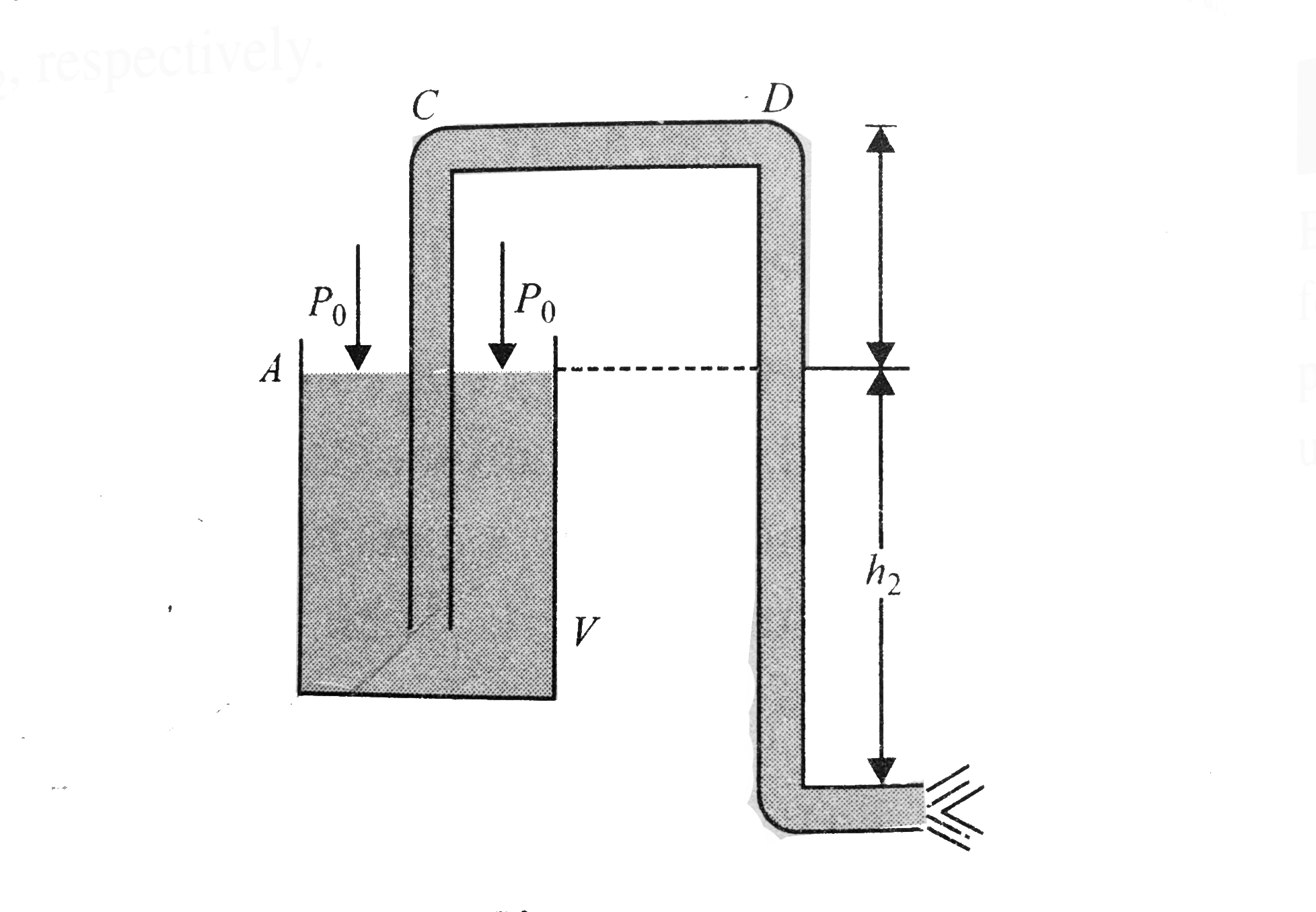
Given h1=h2=3.0m, the gauge pressure of water in the highest level CD of the tube will beA3.0×104N/m2B5.9×104N/m2C5.9×104N/m2D1.5×104N/m2
During blood transfusion the needle is inserted in a veinn where the gauge pressure is 2000 Pa. At what height must the blood container be placed so that blood may just enter the vein? [density of hole blood =1.06×103kgm−3]
(a). 0.192
(b). 0.182
(c). 0.172
(d). 0.162
View SolutionDuring which stage of the cardiac cycle, tricuspid and bicuspid valves are pushed open by the pressure in the atria exerted by the blood emptied into them by the veins
View SolutionThe flow of blood in a large artery of an anaeshetized dog is diverted throg]ugh a venturimeter. The wider part of the meter has a cross sectional area equal to that of the artery i.e. 8mm2. The narrower parts has an are 4mm2. The pressure dorp in the artery is 24Pa. what is the speed of the blood in the artery ? Given that density of the blood = 1.06×103kg/m3
View SolutionBlood pressure in Argentinosaurus. (a) If this long-necked, gigantic sauropod had a head height of 18 m and a heart height of 8.0 m, what (hydrostatic) gauge pressure in its blood was required at the heart such that the blood pressure at the brain was 80 torr (just enough to perfuse the brain with blood)? Assume the blood had a density of 1.06×10kg/m3. (b) What was the blood pressure (in torr or mm Hg) at the feet?
View SolutionWilliam Harvey (1578–1657) was one of the early biologists who studied the bodies of humans and animals. He even dissected the bodies and did experiments with the heart and blood vessels. He concluded from his experiments that the blood leaves the heart through the arteries and returns via the veins. However, he could not explain how blood left the arteries to enter the veins. He said there must be some structure between arteries and veins but he could not find them. Marcello Malphigi (1628–1694) later discovered these structures while studying a dead frog's lungs under a microscope.
What is the MOST LIKELY reason why Harvey could NOT find these structures?
View Solution
