Earthquakes at two places P and Q were measured by a seismograph which recorded the magnitude as 2 and 6. The magnitude of tremors at P and Q can be compared as
Tremors at Q are three times those at place P
Tremors at Q are six times those at place P
Tremors at Q are 1000 times those at place P
Tremors at Q are 10000 times those at place P
The correct Answer is:D
To compare the magnitudes of tremors at places P and Q, we can follow these steps:
1. Understanding the Magnitude Scale:
The magnitude of an earthquake is measured on a logarithmic scale. This means that each whole number increase on the scale represents a tenfold increase in measured amplitude and roughly 31.6 times more energy release.
2. Identify the Magnitudes:
- Magnitude at P (M_P) = 2
- Magnitude at Q (M_Q) = 6
3. Calculate the Difference in Magnitude:
The difference in magnitude between Q and P is:
MQ−MP=6−2=4
4. Calculate the Ratio of Tremors:
Since the scale is logarithmic, the ratio of the tremors can be calculated using the formula:
Tremor at Q=10(MQ−MP)×Tremor at P
Substituting the values:
Tremor at Q=10(6−2)×Tremor at P=104×Tremor at P
5. Conclusion:
This means that the tremor at Q is 10,000 times stronger than the tremor at P. Therefore, we can conclude that:
Tremor at Q=104×Tremor at P
Final Answer:
The tremor at Q is 10,000 times greater than the tremor at P.
---
The magnitude of an earthquake is measured on a logarithmic scale. This means that each whole number increase on the scale represents a tenfold increase in measured amplitude and roughly 31.6 times more energy release.
- Magnitude at P (M_P) = 2
- Magnitude at Q (M_Q) = 6
The difference in magnitude between Q and P is:
MQ−MP=6−2=4
Since the scale is logarithmic, the ratio of the tremors can be calculated using the formula:
Tremor at Q=10(MQ−MP)×Tremor at P
Substituting the values:
Tremor at Q=10(6−2)×Tremor at P=104×Tremor at P
This means that the tremor at Q is 10,000 times stronger than the tremor at P. Therefore, we can conclude that:
Tremor at Q=104×Tremor at P
The tremor at Q is 10,000 times greater than the tremor at P.
Topper's Solved these Questions
- NSO MODEL TEST PAPER -1BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - NSO MODEL TEST PAPER -1EXERCISE - ACHIEVERS SECTION
2 Videos
- LIGHTBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - LIGHTEXERCISE - ACHIEVERS SECTION (HOTS)
5 Videos
- NSO QUESTION PAPER 2017-18 SET-ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - NSO QUESTION PAPER 2017-18 SET-AEXERCISE - ACHIEVERS SECTION
3 Videos
Similar Questions
Two forces of equal magnitude F act on two isolated bodies P and Q as shown in the figure. The mass of body Q is three times that of body P. The magnitude of the acceleration of P is

View SolutionThree point charges -Q, Q and Q are placed on a straight line with distance d between charges as shown. Find the magnitude of the electric field at the point P in the configuration shown which is at a distance a from middle charge Q in the system provided that a>>d. Take 2Qd=p.

View Solution
Knowledge Check
Earthquake at two place I and II were measured by a seismograph and recorded as 2 and 4. What is the magnitude of tremors and its destructive energy at I and II?
ATrenor at II are two time that at place 'I'BTremor at II are four time that at place 'I'.CTremor at II are 100 times that at place 'I'.DTremor at II are 1000 times that at place 'I'.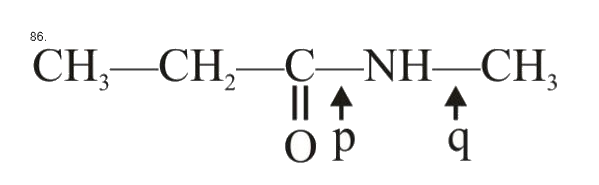
compare the bond length p and q:-Ap=qBq>pCp>qDNot predictedThe resultant of two vectors →A and →b is perpendicular to the vector →A and its magnitude is equal to half the magnitude of vector →B. The angle between →A and →B is
A30∘B45∘C150∘D120∘
The resultant of two forces P and Q makes an angle of 30∘ with P. What is the angle between P and Q, if the magnitude of the resultant is equal to Q√3 ?
View SolutionTwo solenoids acting as short bar magnets P and Q are arranged such that their centres are on the X-axis and are separated by a large distance. The magnetic axes of P and Q are along X and Y-axes, respectively. At a point R, midway between their centres, if B is the magnitude of induction due to Q , then the magnitude of total induction at R due to the magnitude is
View SolutionWhat is the angle between two forces of equal magnitude P, if the magnitude of their resultant is P2 ?
View SolutionGiven →P=2ˆi−3ˆj+4ˆkand→Q=ˆj−2ˆk. The magnitude of their resultant is
View SolutionIf the line of action of the resultant of two forces P and Q divides the angle between them in the ratio 1:2 then the magnitude of the resultant is
View Solution
