A tank 4 m high is half fi lled with water and then filled to the top with oil of density 0.60 g/cc. What is the pressure at the bottom of the tank due to these liquids ? (Take g=10ms−2)
1.6×103Nm−2
3.2×103Nm−2
1.6×104Nm−2
3.2×104Nm−2
The correct Answer is:D
To find the pressure at the bottom of a tank filled with water and oil, we can follow these steps:
Step 1: Understand the tank setup
The tank is 4 meters high. It is half-filled with water (2 meters) and the remaining half (2 meters) is filled with oil.
Step 2: Identify the densities
- Density of water (ρ_water) = 1 g/cm³ = 1000 kg/m³
- Density of oil (ρ_oil) = 0.60 g/cm³ = 600 kg/m³
Step 3: Calculate the pressure due to oil
The pressure at the bottom of the tank due to the oil can be calculated using the formula:
Poil=hoil×ρoil×g
Where:
- hoil = height of the oil = 2 m
- ρoil = density of oil = 600 kg/m³
- g = acceleration due to gravity = 10 m/s²
Substituting the values:
Poil=2m×600kg/m3×10m/s2
P_{\text{oil}} = 12000 \, \text{Pa} \, \text{(or N/m²)}
Step 4: Calculate the pressure due to water
The pressure at the bottom of the tank due to the water can be calculated similarly:
Pwater=hwater×ρwater×g
Where:
- hwater = height of the water = 2 m
- ρwater = density of water = 1000 kg/m³
Substituting the values:
Pwater=2m×1000kg/m3×10m/s2
Pwater=20000Pa(or N/m²)
Step 5: Calculate the total pressure at the bottom of the tank
The total pressure at the bottom of the tank is the sum of the pressure due to oil and the pressure due to water:
Ptotal=Poil+Pwater
Ptotal=12000Pa+20000Pa
Ptotal=32000Pa
Step 6: Convert to standard form
Expressing the total pressure in standard form:
Ptotal=3.2×104Pa
Final Answer
The pressure at the bottom of the tank is 3.2×104N/m2.
---
The tank is 4 meters high. It is half-filled with water (2 meters) and the remaining half (2 meters) is filled with oil.
- Density of water (ρ_water) = 1 g/cm³ = 1000 kg/m³
- Density of oil (ρ_oil) = 0.60 g/cm³ = 600 kg/m³
The pressure at the bottom of the tank due to the oil can be calculated using the formula:
Poil=hoil×ρoil×g
Where:
- hoil = height of the oil = 2 m
- ρoil = density of oil = 600 kg/m³
- g = acceleration due to gravity = 10 m/s²
Poil=2m×600kg/m3×10m/s2
P_{\text{oil}} = 12000 \, \text{Pa} \, \text{(or N/m²)}
The pressure at the bottom of the tank due to the water can be calculated similarly:
Pwater=hwater×ρwater×g
Where:
- hwater = height of the water = 2 m
- ρwater = density of water = 1000 kg/m³
Pwater=2m×1000kg/m3×10m/s2
Pwater=20000Pa(or N/m²)
The total pressure at the bottom of the tank is the sum of the pressure due to oil and the pressure due to water:
Ptotal=Poil+Pwater
Ptotal=12000Pa+20000Pa
Ptotal=32000Pa
Expressing the total pressure in standard form:
Ptotal=3.2×104Pa
The pressure at the bottom of the tank is 3.2×104N/m2.
Topper's Solved these Questions
Similar Questions
A water tank is 20 m deep . If the water barometer reads 10 m at the surface , then what is the pressure at the bottom of the tank in atmosphere ?
View SolutionIf pressure at the half depth of a lake is equal to 34 times the pressure at its bottom, then find the depth of the lake. [Take g = 10 m/s2]
View Solution
Knowledge Check
A tank 5 m high is half filled with water and then is filled to the top with oil of density 0.85 g The pressure at the bottom of the tank, due to these liquids is
A1.85g/cm2B89.25g/cm2C462.5g/cm2D500g/cm2A tank 5 m high is half filled with water and then is filled to top with oil of density 0.85g/cm3 The pressure at the bottom of the tank, due to these liquids is
A1.85g/cm2B89.25g/cm2C462.5g/cm2D500g/cm2A hole is made at the bottom of the tank filled with water (density =1000kgm−3). If the total pressure at the bottom of the tank is three atmospheres (1 atmosphere =105Nm−2), then the velocity of efflux is nearest to
A√400ms−1B√200ms−1C√600ms−1D√500ms−1
A rectangular tank is 10m long 5m broad and 3m high. It is filled to the rim with water of density 103kgm−3. Calculate the thrust at the bottom and walls of the tank due to hydrostatic pressure. Take g=9.8ms−2.
View SolutionA cylinder of 4 m height is half filled with oil of density 0.72 g cm−3. If the Becond half of cylinder is filled with water, then find the pressure at the bottom of cylinder due to these liquids.
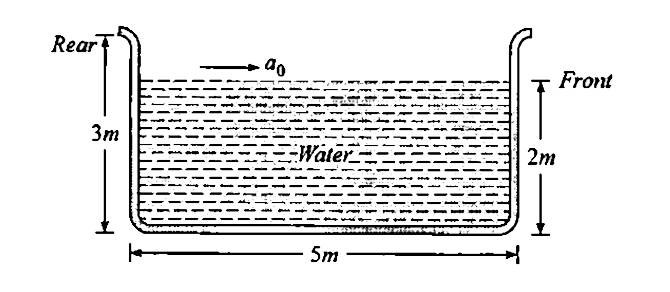
View SolutionAn open reactangular tank with tank with dimensions 5×4m×3m contains water upto a height of 2m is accelerated horizontally along the longer life.
(a) Determine the maximum acceleration that can be given without spilling the water.
(b) If this acceleration is inscreased by 20%. Calculate the percentage of water spilt over.
(c) If initially,the tank is closed at the top and is accelerated horizontally by 9m/s2,find the gauge pressure at the bottom of the front and rear walls of the tank. (g=10m/s2)
View SolutionAn empty cylindrical tank having diameter 5 m is filled with water through a hose pipe having radius 25 cm. If pressure at the bottom of the container increases at a rate of 103Pa s−1, calculate the speed of water flowing through the hose pipe.
(Take g 10 m s−2)
View SolutionA tank is filled with water of density 1gcm−3 and oil of density 0.9gcm−3 . The height of the water layer is 100 cm and of the oil layer is 400 cm. If g = 980 cms−2 , then the velocity of efflux from an opening in the bottom of the tank is
View Solution
