Explain angular velocity and angular acceleration about fixed axis and derive the equation of rotational motion and write the analogy between the equations of linear motion and rotational motion.
 Solution in Gujrati
Solution in Gujrati
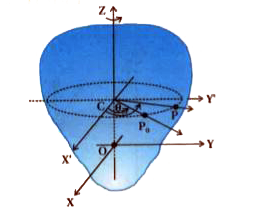
As shown in the figure a rigid body rotating about fixed Z-axis in XYZ cartesion co-ordinate system.
Any particle P of the body circulating in XY-plane.
The angular position of this particle P at t=0 time is θ0 and t=t time it is θ0+θ
∴ In time t its angular displacement is θ.
Now select X. and Y. parallel to X and Y. Z-axis is already fixed.
Intrateneous angular velocity
ω = time rate of change of angular displacement
∴ω=dθdt, is in the direction of fixed Z-axis so it can be taken as scaler.
Angular acceleration α = time rate of change of angular velocity.
α=dωdt, is in the direction of fixed axis so it can be also taken as scalar.
Equations of pure linear motion
v=v0+at
x=x0+v0t+12at2
v2=v20+2a(x−x0)
where x0 = initial position
x = final position
v0 = initial velocity
v = final velocity
a = acceleration, t = time
Equation of pure rotational motion
ω=ω0+at
θ=θ0+ω0t+12αt2
ω2=ω20+2α(θ−θ0)
where θ0 = Initial angular position
θ = Final angular position
ω0 = Initial angular velocity
ω = Final angular velocity
α = Angular acceleration
t = time
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-A HOTS
3 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-A (TRY YOURSELF (VSQs))
94 Videos
- QUESTIONS ASKED IN JEE - 2020 BOOK - KUMAR PRAKASHANCHAPTER - QUESTIONS ASKED IN JEE - 2020 EXERCISE - Question
16 Videos
- THERMAL PROPERTIES OF MATTERBOOK - KUMAR PRAKASHANCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks
1 Videos
Similar Questions
What is torque? Explain the torque acting on a particle.
View SolutionWhat is a rigid body ? Explain the differences between rigid body and solid body.
View SolutionA non-isotropic solid metal cube has coefficient of linear expansion as 5×10−5/∘C along the x-axis and 5×10−6/∘C along y-axis and z-axis. If the coefficient of volumetric expansion of the solid is n×10−6/∘C then the value of n is....
View SolutionIn an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150∘C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27∘C. The final temperature is 40∘C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal ?
View SolutionWrite the equations of motion for a particle rotating about a fixed axis.
View SolutionCompare the equations of linear motion with rotational motion .
View SolutionDistinguish between kinetic equation for linear and angular motion .
View SolutionDynamics of rotational Motion about fixed axis of rotation
View Solution.......... in linear motion is analogous to moment of inertia in rotational motion.
View SolutionRotational Motion | Relation Between Angular Velocity And Linear Velocity
View SolutionRotational Motion | Angular Momentum Of A Body Rotating About Fixed Axis.
View SolutionKinematics of Rotational motion|Dynamics of rotational motion #!# Angular momentum in case of rotation about a fixed axis
View SolutionKinematics of Rotational Motion|Dynamics of rotational Motion #!# Angular momentum in rotation about a fixed axis#!#NEET important and Previous Years Questions
View SolutionRelation between linear and angular velocity for object in rotational motion is →v=→r×→ω
View SolutionRelation between linear and angular velocity for object in rotational motion is →v=→r×→ω
View Solution
