Explain the equivalent resistance of a series and parallel resistor network. Solution in Tamil

Resistor in series: When two or more resistors are connected end to end, they are said to be in series. The resistors could be simple resistors or bulbs or heating elements or other devices. Fig. (a) shows three resistors R1,R2andR3 connected in series.
The amount of charge passing through resistor R2 must also pass through resistors R2andR3 since the charges cannot accumulate anywhere in the circuit. Due to this reason, the current I passing through all the three resistors is the same. According to Ohm.s law, if same current pass through different resistors of different values, then the potential difference across each resistor must be different. Let V1,V2andV3 be the potential difference (voltage) across each of the resistors R1,R2andR3 respectively, then we can write V1=IR1,V2=IR2andV3=IR3. But the total voltage V is equal to the sum of voltages across each resistor.
V=V1+V2+V3
=IR1+IR2+IR3 ...(1)
V=I(R1+R2+R3)
V+I.Rs ...(2)
where Rs is the equivalent resistance,
Rs=R1+R2+R3 ...(3)
When several resistances are connected in series, the total or equivalent resistance is the sum of the individual resistances as shown in fig.(b).
Note: The value of equivalent resistance in series connection will be greater than each individual resistance.
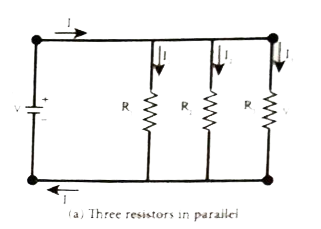
Resistors in parallel: Resistors are in parallel when they are connected across the same potential difference as shown in fig. (a).
In this case, the total current I that leaves the battery in split into three separate paths. Let I1,I2andI3 be the current through the resistors R1,R2andR3 respectively. Due to the conservation of charge, total current in the circuit I is equal to sum of the currents through each of the three resistors.
I=I1+I2+I3 ...(1)
Since the voltage across each resistor is the same, applying Ohm.s law to each resistor, we have
I1=VR1,I2=VR2,I3=VR3 ...(2)
Substituting these values in equation (1), we get
I=VR1+VR2+VR3=V[1R1+1R2+1R3]
I=VRp
1Rp=1R1+1R2+1R3 ...(3)
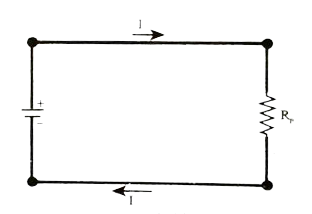
Here Rp is the equivalent resistance of the parallel combination of the resistors. Thus, when a number of resistors are connected in parallel, the sum of the reciprocal of the values of resistance of the individual resistor is equal to the reciprocal of the effective resistance of the combination as shown in the fig. (b).
Note: The value of equivalent resistance in parallel connection will be lesser than each individual resistance.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - FULL MARKSCHAPTER - CURRENT ELECTRICITYEXERCISE - TEXTBOOK EVALUATION (Numerical Problems)
15 Videos
- CURRENT ELECTRICITYBOOK - FULL MARKSCHAPTER - CURRENT ELECTRICITYEXERCISE - Additional Questions Solved (Choose the correct answer)
41 Videos
- CURRENT ELECTRICITYBOOK - FULL MARKSCHAPTER - CURRENT ELECTRICITYEXERCISE - TEXTBOOK EVALUATION (Short Answer Questions)
21 Videos
- COMMUNICATION SYSTEMSBOOK - FULL MARKSCHAPTER - COMMUNICATION SYSTEMSEXERCISE - ADDITIONAL QUESTIONS (Additional problems)
3 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - FULL MARKSCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ADDITIONAL QUESTIONS -( ADDITIONAL NUMERICAL PROBLEMS : )
10 Videos
Similar Questions
The following graphs represent the current versus voltage and voltage versus current for the six conductors A,B,C,D,E and F. Which conductor has least resistance and which has maximum resistance?
View SolutionWhen current I flows through a wire, the drift velocity of the electrons is v. When current 2I flows through another wire of the same material having double the length and area of cross-section, the drift velocity of the electrons will be
View SolutionWhy current is a scalar?
View SolutionA radio can tune into any station in the 7.5 MHz to 12 MHz band. What is the corresponding wavelength band ?
View SolutionIf a light of wavelength 4950 Å is viewed as a continuous flow of photons, what is the energy of each photon in eV ? (Given h=6.6×10−34Js, c =3×108ms−1)
View SolutionThe equivalent resistance of n identical resistors connected in parallel si x. If the resistors are connected in series, the equivalent resistance would be.
View SolutionThe equivalent resistance of two resistors connected in series 6Ω and their parallel equivalent resistance is 43Ω. What are the value of resistance?
View Solutionश्रेणी तथा समान्तर - क्रमो में प्रतिरोधों के संयोजन का तुल्य - प्रतिरोध ज्ञात करना ।
View SolutionExplain the equivalent resistance of a series and parallel resistor network.
View SolutionDefine effective resistance of a number of resistors connected in a series or parallel combination
View SolutionExplain the equivalent resistance of a series and parallel resistor network.
View SolutionExplain the equivalent resistance of a series and parallel resistor network.
View SolutionFind the equivalent resistance of the two resistors connected in parallel series.
View SolutionThe equivalent resistance of network of three 2Ω resistors can not be
View SolutionThe equivalent resistance of network of three 4Omega resistors can not be
View Solution
