Explain the formation of stationary waves in an air column enclosed in open pipe. Derive the equations for the frequencies of the harmonics produced.

Text Solution

Verified by Experts

Formation of stationary wave in open pipe : An open pipe is a cylindrical tube having air inside with both ends open.
Let a longitudinal wave pass through the organ.pipe. It gets reflected at the end of the pipe. These incident and reflected . waves which are of same frequency, travelling in opposite directions, get superposed along the length of the pipe.
As a result of it, longitudinal stationary waves are formed.
At the open end, the particles of the medium are free to vi brate and the incident and reflected waves will be in phase, so particles have maximum displacement, forming antinode. Thus the air column inside a open pipe is set into vibration due to stationary waves formed in it with antinode at each open end.
Harmonics in open pipe :
Fundamental : In the fundamental mode of vibration, an antin ode is formed at each end and a node is formed between them. The note produced is called first harmonic
If .l.. is the vibrating length and $λ_{1}$ is the corresponding wave length.
$l = \frac{λ_{1}}{2} \Rightarrow λ_{1} = 2 l$
Fundamental frequency $u_{1} = \frac{v}{λ_{1}}$
$∴ u_{1} = \frac{v}{2 l}$

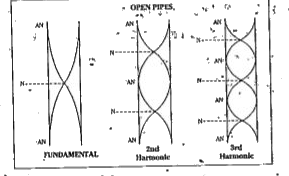
Second Harmonic (or) first overtone : 2nd harmonic consists of three antinodes and two nodes.
If $λ_{2}$ is the corresponding wavelength
$l = \frac{λ_{2}}{4} + \frac{λ_{2}}{2} + \frac{λ_{2}}{4} = λ_{2} \Rightarrow l = λ_{2}$
$∴ u_{2} = \frac{v}{λ_{2}} = \frac{v}{l} = 2 \times \frac{v}{2 l} = 2 v_{1}$
Third harmonic or Second overtone : 3rd harmonic consists of four antinodes and three nodes. If $λ_{3}$ is the corresponding wave length
$l = \frac{λ_{3}}{4} + \frac{λ_{3}}{2} + \frac{λ_{3}}{2} + \frac{λ_{3}}{4} = \frac{3 λ_{3}}{2}$
$λ_{3} = \frac{2 l}{3} ∴ u_{3} \frac{v}{λ_{3}} (O R) u_{3} = \frac{3 v}{2 l} u_{3} = 3 u_{1}$
The ratio of harmonics in open pipes $u_{1} : u_{2} : u_{3} := 1 : 2 : 3 :$ ......
Length of closed organ pipe l = 70 cm
Velocity of sound $v = 331 m s^{- 1}$
Fundamental frequency of closed pipe
$u = \frac{v}{4 l} = \frac{331}{4 \times 70 \times 10^{- 2}} = \frac{331}{280 \times 10^{- 2}}$
$∴ n = \frac{331 \times 10^{2}}{280} = n = (118.2 H z)$

Updated on:21/07/2023

In the stationary waves in an open organ pipe -
ABoth the ends are antinodes and in between them there is at least one node
BBoth the ends are nodes and in between them there is at least one antinode
CAntinode at one end and node at the other
DBoth the ends are antinodes and in between them there is no node
In the stationary waves in an open organ pipe -
ABoth the ends are antinodes and in between them there is at least one node
BBoth the ends are nodes and in between them there is at least one antinode
CAntinode at one end and node at the other
DBoth the ends are antinodes and in between them there is no node.
Stationary waves in closed pipe will produce
Aall the harmonics.
Ball the even harmonics.
Call the odd harmonics.
Dno harmonics.