How are Stationary waves formed in closed pipes and open pipes ? Explain the various modes of vibrations and obtain relations for their frequencies.
Text Solution
A closed pipe is a cylindrical tube having air inside it with one end closed and the other end open.
Let-a longitudinal wave be sent through a closed pipe. It gets reflected at the closed end of the pipe. These incident and reflected waves, which are of same frequency, travelling in opposite directions gets superposed as a result longitudinal stationary waves are formed.
At the closed end reflection is on a rigid surface a node is formed at closed end, at the open end antinode is formed.
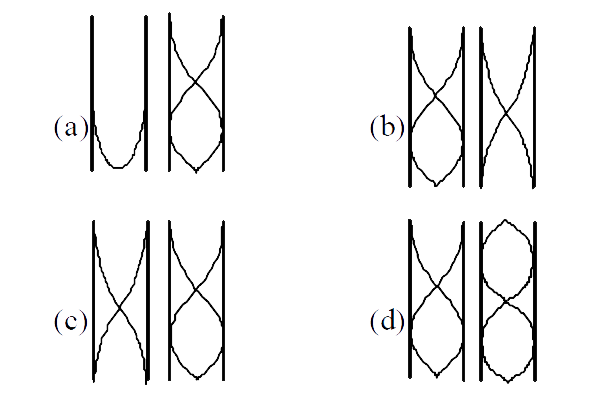
I. Harmonics in a closed pipe:
Fundamental mode (or) First Harmonic:
In this one .node and one antinode is formed. Ify is the vibrating length and λ1 is the corresponding wavelength.
I=λ14 because the distance between a node and next antinode is λ4
λ1=4l
The fundamental frequency
υ1=vλ1⇒υ1=v4l
II. First overtone or 2nd Harmonic:
1st overtone consists of two nodes and two antinodes are formed. If .l. is the vibrating length and λ3 is the corresponding wavelength, l=λ4+λ2.
The frequency of the first overtone or 3rd harmonic
υ3=vλ3=3v4l,(υ3)=3υ1
III. Fifth Harmonic or 3rd overtone:
2nd overtone consists of three nodes and three antinodes are formed.
If ‘l’ is the vibrating length, λ5 is the corresponding wavelength,
l=λ54+λ52+(λ2)=5λ54,
∴ The frequency of second overtone or 5th harmonic
υ5=vλ5⇒υ5=5v4l,υ5=5υ1
In closed pipe Harmonics are in the ratio = 1:3:5:7 ........
In closed pipe only odd Harmonics are formed.

Harmonics in open pipe :
In the fundamental mode of vibration, an antinode is formed at each end with a node in between them.
If ‘l’ is the vibrating length and λ1 is the corresponding wavelength. l=λ12.
The frequency of fundamental mode υ1=vλ1∴υ1=v2l

Second Harmonic or first overtone: It will have three antinodes and two nodes.
If λ2 iis the corresponding wavelength
l=λ24+λ24+λ24=λ2⇒l=λ2
∴υ2=vλ2=vl=2×v2l=2υ1

Third harmonic or Second overtone:
It will have four antinodes and three nodes. If λ3 is the corresponding wavelength,
l=λ34+λ32+λ32+λ34=3λ32
λ3=2l3,∴υ3=vλ3υ3=3v2lυ3=3υ1
In open pipe harmonics are in the ratio of 1:2:3....
|
Topper's Solved these Questions
- MODEL PAPER - 10 (PAPER - II)BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER - 10 (PAPER - II)EXERCISE - Section - B
8 Videos
- MODEL PAPER 4BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 4EXERCISE - SECTION - C
5 Videos
- MODEL PAPER - 13BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER - 13EXERCISE - Section - C
3 Videos
Similar Questions
Knowledge Check
Stationary waves in closed pipe will produce
Aall the harmonics.Ball the even harmonics.Call the odd harmonics.Dno harmonics.In the stationary waves in an open organ pipe -
ABoth the ends are antinodes and in between them there is at least one nodeBBoth the ends are nodes and in between them there is at least one antinodeCAntinode at one end and node at the otherDBoth the ends are antinodes and in between them there is no nodeIn the stationary waves in an open organ pipe -
ABoth the ends are antinodes and in between them there is at least one nodeBBoth the ends are nodes and in between them there is at least one antinodeCAntinode at one end and node at the otherDBoth the ends are antinodes and in between them there is no node.
Describe analytically how standing waves are formed in closed organ pipes. Also discuss normal modes of vibration of the pipes.
View SolutionDraw diagrams to show the various modes of vibration in (i) an open pipe and (ii) a closed pipe.
View SolutionDraw the fundamental modes of vibration of stationary waves in : An open pipe.
View SolutionModes of vibration in a closed organ pipe are represented by –
View SolutionModes of vibration in an open organ pipe are represented by –
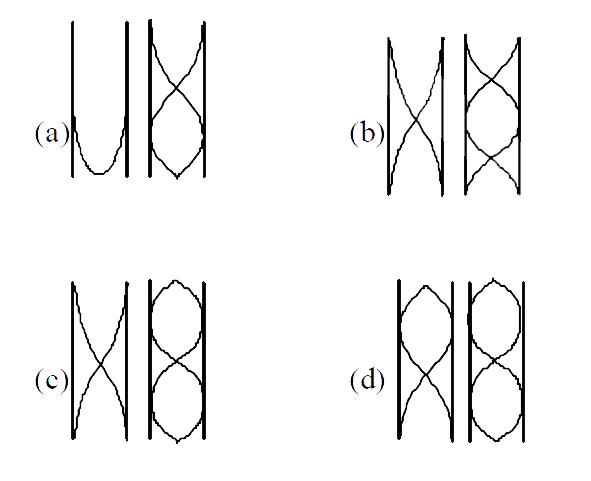
View Solution
