Explain the use of a metre bridge for finding unknown resistance.
To explain the use of a metre bridge for finding an unknown resistance, we can follow these steps:
1. Understanding the Meter Bridge Setup:
- A metre bridge consists of a uniform wire of length 1 meter, mounted on a wooden base with a scale. It has two gaps where resistances can be connected.
2. Connecting the Circuit:
- Connect a known resistance (R) from one gap (let's call it gap A) and the unknown resistance (S) from the other gap (gap B). A galvanometer is connected between a point on the wire and a jockey (a movable contact).
3. Finding the Null Point:
- When the jockey is moved along the wire, a point is found where the galvanometer shows no deflection. This point is known as the "null point," indicating that the bridge is balanced.
4. Using the Principle of Wheatstone Bridge:
- At the null point, the ratio of the lengths of the wire segments (P and Q) is equal to the ratio of the resistances connected in the gaps. This can be expressed as:
PQ=RS
- Here, P is the length of the wire from one end to the null point, and Q is the length from the null point to the other end.
5. Calculating the Unknown Resistance:
- If L is the length of the wire from the left end to the null point (P), then the length from the null point to the right end (Q) can be expressed as (100 - L) cm (since the total length is 100 cm).
- Rearranging the equation gives:
S=R⋅(100−L)L
- This formula allows us to calculate the unknown resistance (S) using the known resistance (R) and the measured lengths.
6. Conclusion:
- By adjusting the known resistance and finding the corresponding null point, we can accurately determine the value of the unknown resistance using the metre bridge.
- A metre bridge consists of a uniform wire of length 1 meter, mounted on a wooden base with a scale. It has two gaps where resistances can be connected.
- Connect a known resistance (R) from one gap (let's call it gap A) and the unknown resistance (S) from the other gap (gap B). A galvanometer is connected between a point on the wire and a jockey (a movable contact).
- When the jockey is moved along the wire, a point is found where the galvanometer shows no deflection. This point is known as the "null point," indicating that the bridge is balanced.
- At the null point, the ratio of the lengths of the wire segments (P and Q) is equal to the ratio of the resistances connected in the gaps. This can be expressed as:
PQ=RS
- Here, P is the length of the wire from one end to the null point, and Q is the length from the null point to the other end.
- If L is the length of the wire from the left end to the null point (P), then the length from the null point to the right end (Q) can be expressed as (100 - L) cm (since the total length is 100 cm).
- Rearranging the equation gives:
S=R⋅(100−L)L
- This formula allows us to calculate the unknown resistance (S) using the known resistance (R) and the measured lengths.
- By adjusting the known resistance and finding the corresponding null point, we can accurately determine the value of the unknown resistance using the metre bridge.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MBD -HARYANA BOARDCHAPTER - CURRENT ELECTRICITYEXERCISE - OBJECTIVE TYPE QUESTIONS
20 Videos
- CURRENT ELECTRICITYBOOK - MBD -HARYANA BOARDCHAPTER - CURRENT ELECTRICITYEXERCISE - SHORT ANSWER TYPE QUESTIONS
9 Videos
- BOARD QUESTION PAPER (SOLVED) - 2019BOOK - MBD -HARYANA BOARDCHAPTER - BOARD QUESTION PAPER (SOLVED) - 2019EXERCISE - LONG ANSWER TYPE QUESTIONS
4 Videos
- DUAL NATURE OF MATTER AND RADIATIONSBOOK - MBD -HARYANA BOARDCHAPTER - DUAL NATURE OF MATTER AND RADIATIONSEXERCISE - OBJECTIVE TYPE QUESTIONS
17 Videos
Similar Questions
Knowledge Check
During an experiment with a metre bridge, the galvanometer shows a null point when the jockey is pressed at 40.0cm using a standard resistance of 90Ω, as shown in the figure. The least count of the scale used in the metre bridge is 1mm. The unknown resistance is
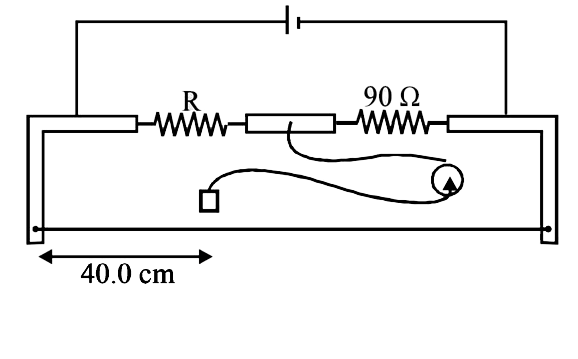 A60±0.15ΩB135±0.56ΩC60±0.25ΩD135±0.23Ω
A60±0.15ΩB135±0.56ΩC60±0.25ΩD135±0.23ΩConsider a metre bridge whose length of wire is 2m. A resistance of 10Ω is connected across one gap of the meter bridge and an unknown resistance is connected across the other gap. When these resistances are interchanged, the balance point shifts by 50 cm. What is the value of the unknown resistance?
A250ΩB10ΩC16.7ΩDNone of the aboveIn a metre bridge , the balancing length from the left end is found to be 40cm, when a known resistance of 3Ω is placed in the right gap, then the value of unknown resistance is
A1ΩB2ΩC3ΩD4Ω
Draw the circuit diagram to determine unknown resistance using meter bridge. Write the equation used for determining the unknown resistance.
View SolutionAn unknown resistance 'X' is placed in the left gap and and a known resistance of 60Ω is plaecd in the right gap of metre bridge. The null point is obtained at 40 cm from the left end fo the bridge. Fid the unknown resistance.
View SolutionPotentiometer and metre bridge
View SolutionTwo equal resistance are connected in the gaps of a metre bridge. If the resistance in the left gap is increased by 10% the balancing point shift
View SolutionTwo equal resistance are connected in the gaps of a metre bridge. If the resistance in the left gap is increased by 10% the balancing point shift
View Solution
