Explain velocity gradient and coefficient of viscous and gives their units.Solution in Gujrati
Let laminar floe on a horizontal surface as shown in figure
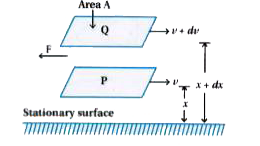
Suppose two layer P and Q at distance x and x+dx from stationary surface.
The velocity difference dv between two layers separated by distance dx.
is know as velocity gradient.
Velocity gradient : The difference in velocity between adjacent layers of the fluid is known as a velocity gradient.
Viscous force between two layers depend on following factors .
(1) Depends on the area (A) of two contact surface .
..... (1)
(2) Velocity gradient between two layers
......(2)
....(3)
.....(4)
Here is known as coefficient of viscosity .Its magnitude depend on the kind of fluid and on temperature.
Negative sing indicates viscosity force , is opposite to the velocity of layers of fluid.
As the temperature increase in liquid will be decrease while in gas it increases.
In equation (4), A=1 unit, then .
Definition of coefficient of viscosity :
The viscous force acting per unit surface area of contact and per unit velocity gradient between two adjacent layers in a laminar flow is known as the coefficient of viscosity .
Unit of coefficient of viscosity :
(1) CGS unit of viscosity is dyne
or . It is called poise.
MKS unit of viscosity is or . It is called decapoise or poisenile.
1 poisenille
=10 poise.
(3) Dimensional formula
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDS BOOK - KUMAR PRAKASHANCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - SECTION-A Try Yourself (VSQs)
132 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - KUMAR PRAKASHANCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - SECTION - B Numericals
29 Videos
- MACHANICAL PROPERTIES OF SOLIDS BOOK - KUMAR PRAKASHANCHAPTER - MACHANICAL PROPERTIES OF SOLIDS EXERCISE - QUESTION PAPER
11 Videos
- MOTION IN A STRAIGHT LINE BOOK - KUMAR PRAKASHANCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - QUESTION PAPER
11 Videos
Similar Questions
What is fluid ?
View SolutionA 14.5 kg mass, fastened to the end of a steel wire of unstretched 1.0 m, is whirled in a vertical circle with an angular velocity of 2 rev/s at the bottom of the circle. The cross- sectional area of the wire is 0.065 cm2. Calculate the elongation of the wire when the mass is at the lowest point of its path.
View SolutionWhat is called brittle material ?
View SolutionDefine frame of reference and give its types.
View SolutionThe viscous force on a spherical body, when it moves through a viscous liquid, depends on the radius of the body, the coefficient of viscosity of the liquid and the velocity of the body.Find an expression for the viscous force.
View SolutionVelocity gradient is \\ defind as ' change in velocity per unit distance . Then its unit in E.P.S system is s^(-1)
View Solutionश्यान-बल क्या है? यह किन-किन बातो पर निर्भर करता है? श्यानता - गुणांक की परिभाषा दीजिए।
View Solutionताप प्रवणता का क्या मात्रक है | इसकी दिशा बताइये |
View SolutionThe S.I. unit and dimensions of velocity gradient is streamline flow is
View Solutionवेग प्रवणता का मात्रक तथा विमीय सूत्र लिखिए |
View SolutionWhen a liquid flows in a tube, there is relative motion between adjacent layers of the liquid. This force is called the viscous force which tends to oppose the relative motion between the layers of the liquid. Newton was the first person to study the factors that govern the viscous force in a liquid. According to Newton’s law of viscous flow, the magnitude of the viscous force on a certain layer of a liquid is given by
F=−ηAdvdx
where A is the area of the layer dvdx is the velocity gradient at the layer and η is the coefficient of viscosity of the liquid.
A river is 5 m deep. The velocity of water on its surface is 2ms−1 If the coefficient of viscosity of water is 10−3Nsm−2 , the viscous force per unit area is :
View SolutionA liquid having coefficient of viscosity 0.02 decapoise is filled in a container of cross-sectional area 20 m^2 viscous drag between two adjacent layers in flowing is 1 N, then velocity gradient is
View SolutionThe viscous force is ______ proportional to the velocity gradient.
View SolutionDefine the velocity gradient and give its units.
View Solution(a) श्यानता गुणांक की परिभाषा और इसका SI मात्रक लिखिए।
(b) अंतिम (टर्मिनल) वेग की परिभाषा कीजिए। किसी श्यान द्रव में गिरते हुए गोले के अंतिम वेग के लिए व्यंजक व्युत्पन्न कीजिए।
View Solution
