F and are the forces exerted by the liquid on the curved surface and at the bottom of a cylindrical vessel (radius r) respectively. To which height should the vessel be filled to make F and f equal?
To solve the problem of determining the height h to which a cylindrical vessel should be filled so that the force F exerted by the liquid on the curved surface equals the force f exerted at the bottom, we can follow these steps:
1. Understand the Forces:
- The force f at the bottom of the cylindrical vessel is due to the pressure exerted by the liquid column above it.
- The force F on the curved surface of the cylinder is due to the varying pressure at different depths.
2. Calculate the Force at the Bottom:
- The pressure at the bottom of the vessel can be expressed as:
P=ρgh
where ρ is the density of the liquid, g is the acceleration due to gravity, and h is the height of the liquid.
- The area of the bottom of the cylinder is:
A=πr2
- Therefore, the force f at the bottom is:
f=P⋅A=ρgh⋅πr2=ρgπr2h
3. Calculate the Force on the Curved Surface:
- The pressure at a depth x is given by:
P=ρgx
- The differential area dA of a ring at depth x with thickness dx is:
dA=2πrdx
- The force dF on this differential area is:
dF=P⋅dA=ρgx⋅2πrdx
- To find the total force F on the curved surface, integrate dF from 0 to h:
F=∫h0ρgx⋅2πrdx=2πrρg∫h0xdx
- The integral of x is:
∫h0xdx=h22
- Thus, the total force F is:
F=2πrρg⋅h22=πrρgh2
4. Set the Forces Equal:
- To find the height h where F=f:
πrρgh2=ρgπr2h
- Cancel out common terms (ρgπr):
h2=rh
- Rearranging gives:
h2−rh=0
- Factoring out h:
h(h−r)=0
- This gives two solutions: h=0 or h=r.
5. Conclusion:
- The height h to which the vessel should be filled to make F and f equal is:
h=r
- The force f at the bottom of the cylindrical vessel is due to the pressure exerted by the liquid column above it.
- The force F on the curved surface of the cylinder is due to the varying pressure at different depths.
- The pressure at the bottom of the vessel can be expressed as:
P=ρgh
where ρ is the density of the liquid, g is the acceleration due to gravity, and h is the height of the liquid.
- The area of the bottom of the cylinder is:
A=πr2
- Therefore, the force f at the bottom is:
f=P⋅A=ρgh⋅πr2=ρgπr2h
- The pressure at a depth x is given by:
P=ρgx
- The differential area dA of a ring at depth x with thickness dx is:
dA=2πrdx
- The force dF on this differential area is:
dF=P⋅dA=ρgx⋅2πrdx
- To find the total force F on the curved surface, integrate dF from 0 to h:
F=∫h0ρgx⋅2πrdx=2πrρg∫h0xdx
- The integral of x is:
∫h0xdx=h22
- Thus, the total force F is:
F=2πrρg⋅h22=πrρgh2
- To find the height h where F=f:
πrρgh2=ρgπr2h
- Cancel out common terms (ρgπr):
h2=rh
- Rearranging gives:
h2−rh=0
- Factoring out h:
h(h−r)=0
- This gives two solutions: h=0 or h=r.
- The height h to which the vessel should be filled to make F and f equal is:
h=r
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Very Short Answer Questions)54videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Additional Questions)3videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Short Answer Type Questions)5videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)12videos
MATHEMATICAL TOOLS
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test15videos
MOTION IN A PLANE
Similar Questions
The force F needed to support the liquid of density ρ and the vessel on it, in figure, is
View SolutionIf water is ejecting from a hole of radius r at a depth h from the water surface in cylindrical vessel of diameter D, then speed with which the water level in the vessel drops .(Consider area of hole is comparable to area of vessel)
View Solution
Knowledge Check
- Question 1 - Select One
Water pours out rate of Q from a tap, into a cylindrical vessel of radius r. The rate at which the height of water level rises the height is h, is
AQπrhBQπr2CQ2πr2DQπr2h - Question 2 - Select One
A cylindrical vessel of radius r is filled with a homogeneous liquid upto a height h. It is found that the force exerted by the liquid column on the bottom of the cylinder is equal to the force exerted by the liquid on the sides of the cylinder. What is the relation between r and h?
Ar=h2Br=hCr=2hDr=32h - Question 3 - Select One or More
In the following figure shown, a liquid is filled into the vessel up to a height h and the forces exerted against the liquid by the walls of the vessel are shown by arrows, the force being everywhere perpendicular to the walls of the vessel. For this situation mark out the correct statement(s).
 AThe horizontal component of the forces on the left and right side inclined faces will cancel each other.BThe weight of the section lettered A is supported by vertical component of forces acting on the inclined faces.CForce exerted by the liquid on the base of the vessel is greater than (p0+ρgh)A where ρ Net force exerted by liquid on the base of the vessel is in the vertical downward direction. is the density of the liquid and A is base area of the vessel.DNet force exerted by liquid on the base of the vessel is in the vertical downward direction.
AThe horizontal component of the forces on the left and right side inclined faces will cancel each other.BThe weight of the section lettered A is supported by vertical component of forces acting on the inclined faces.CForce exerted by the liquid on the base of the vessel is greater than (p0+ρgh)A where ρ Net force exerted by liquid on the base of the vessel is in the vertical downward direction. is the density of the liquid and A is base area of the vessel.DNet force exerted by liquid on the base of the vessel is in the vertical downward direction.
A person looking through a telescope focuses the lens at a point on the edge of the bottom of an empty cylindrical vessel Next he fills the entire vessel with a liquid of refractive index μ, without disturbing the telescope. Now, he observes the midpoint of the bottom of the vessel Determine the radius to depth ratio of the vessel
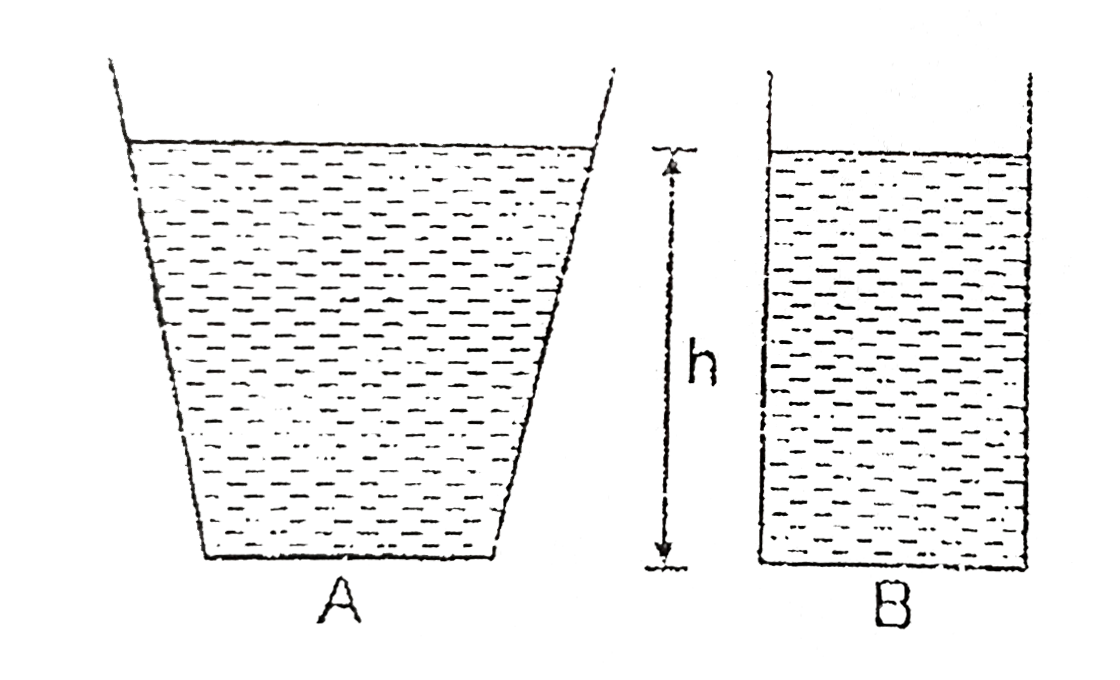
View SolutionTwo vessels A and B of different shapes have the same base area and are filled with water up to the same height h (see figure). The force exerted by water on the base is FA for vessel A and FB for vessel B. The respective weights of the water filled in vessels are WA and WB. Then
 View Solution
View SolutionSome liquid is filled in a cylindrical vessel of radius R. Let F1 be the force applied by the liquid on the bottom of the cylinder. Now the same liquid is poured into a vessel of uniform square cross-section of side R. Let F2 be the force applied by the liquid on the bottom of this new vessel. (Neglect atmosphere pressure). Then
View SolutionTwo vessels A and B of different shapes have the same base area and are filled with water up to the same height h (see figure). The force exerted by water on the base is FA for vessel A and FB for vessel B. The respective weights of the water filled in vessels are WA and WB. Then
 View Solution
View SolutionIn a cylindrical vessel containing liquid of density ρ, there are two holes in the side walls at heights of h1 and h2 respectively such that the range of efflux at the bottom of the vessel is same. The height of a hole, for which the range of efflux would be maximum, will be –
 View Solution
View Solution

