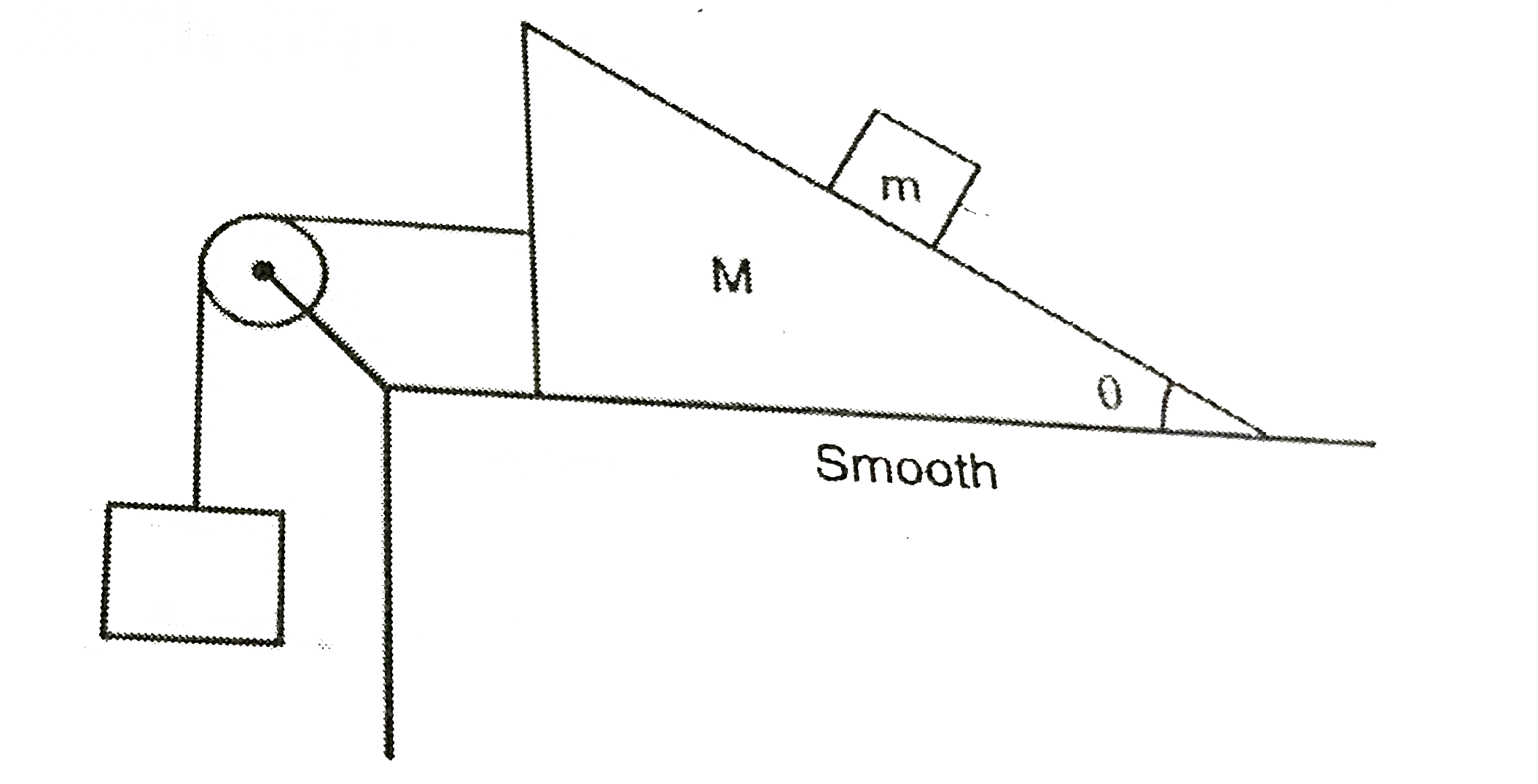
Fig shows a block of mass 0.1kg placed on a smooth wedge of mass 15√3 kg if the block of mass m will move vertically downward with acceleration 10m/s2 Then the value of tension (in newton) in the string is (θ=30∘) :
The correct Answer is:2
Accelerating to the given problem, m is a freely falling body, i.e., contact force between M and m is zero. Under this condition, acceleration of M leftwards will be
a=gcotα=g×√3
Tension T=Ma=15√3×√3g=2N
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Matrix match
7 Videos
- BASIC MATHEMATICSBOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice
35 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
Similar Questions
A block of mass 1 kg and density 0.8g/cm3 is held stationary with the help of a string as shown in figure. The tank is accelerating vertically upwards with an acceleration a =1.0m/s2. Find

(a) the tension in the string,
(b) if the string is now cut find the acceleration of block.
(Take g=10m/s2 and density of water =103kg/m3).
View SolutionA block of mass 5 kg is placed on bus moving with acceleration 2m/s2.pseudo force acting on block as seen by a man on ground is -
View Solution
Knowledge Check
Figure shown a block of mass m placed on a smooth wedge of mass M. Calculate the minimum value of M' and tension in the string, so that the block of mass m will move vertically downwards with acceleration 10ms−2
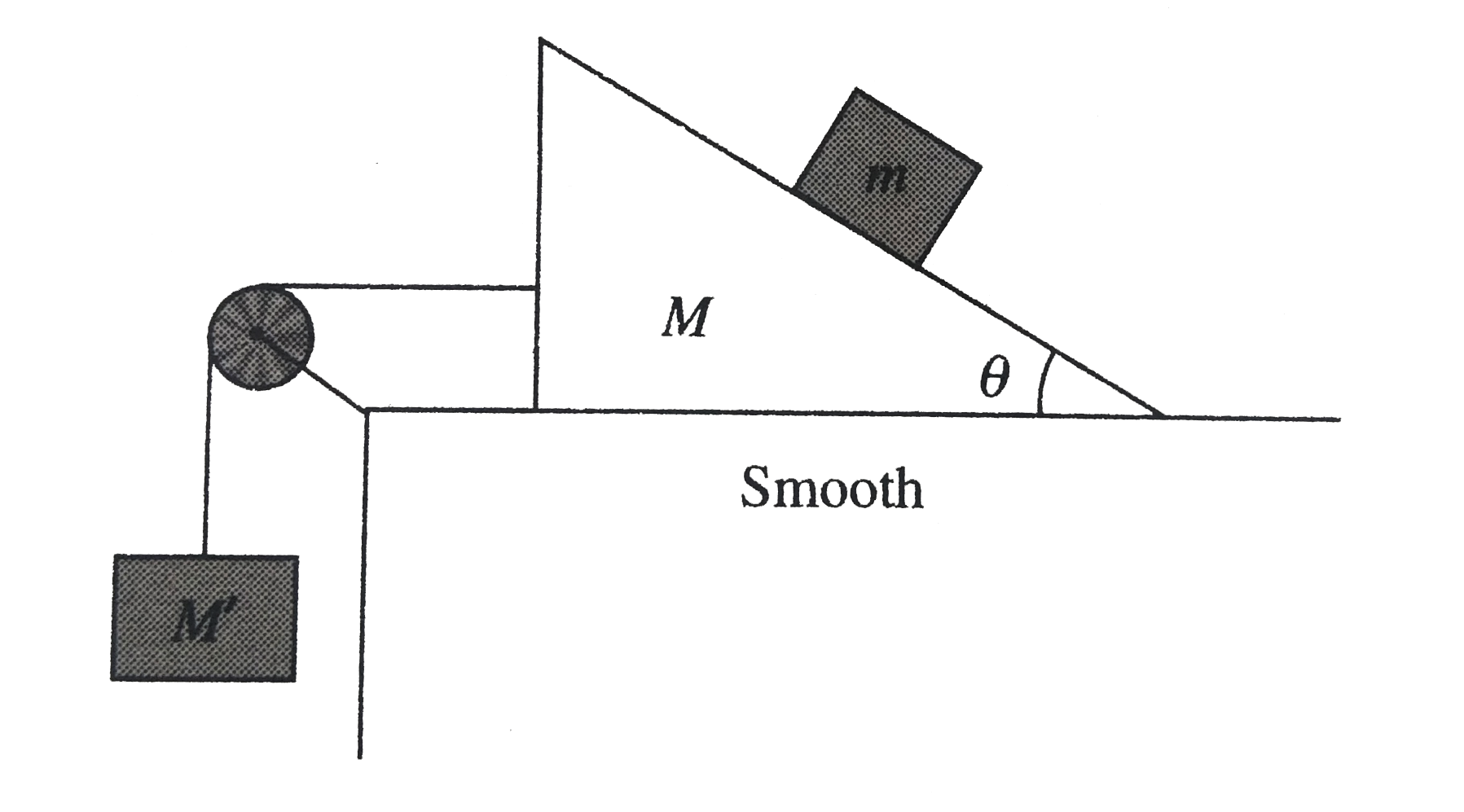 AThe value of M' is Mcotθ1−cotθBThe value of M' is Mtanθ1−tanθCThe value of tension in the string is MgtanθDThe value of tension is Mgcotθ
AThe value of M' is Mcotθ1−cotθBThe value of M' is Mtanθ1−tanθCThe value of tension in the string is MgtanθDThe value of tension is MgcotθA block of mass m is placed on a smooth wedge of inclination θ & mass M. The whole system is slip on the wedge. Then the normal reaction on the wedge acting from the ground :
A(M+m)gB(M+msinθ)gCMgD(M+msinθM+m)gcosθA block of mass m=5 kg is placed on the wedge of mass M=32 kg as shown in the figure. Find the acceleration of wedge with respect to ground. (Neglect any type of friction. String and pulley are ideal )
 A12m/s2B35m/s2C43m/s2D34m/s2
A12m/s2B35m/s2C43m/s2D34m/s2
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
View SolutionIf coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. (g=10m/s2)
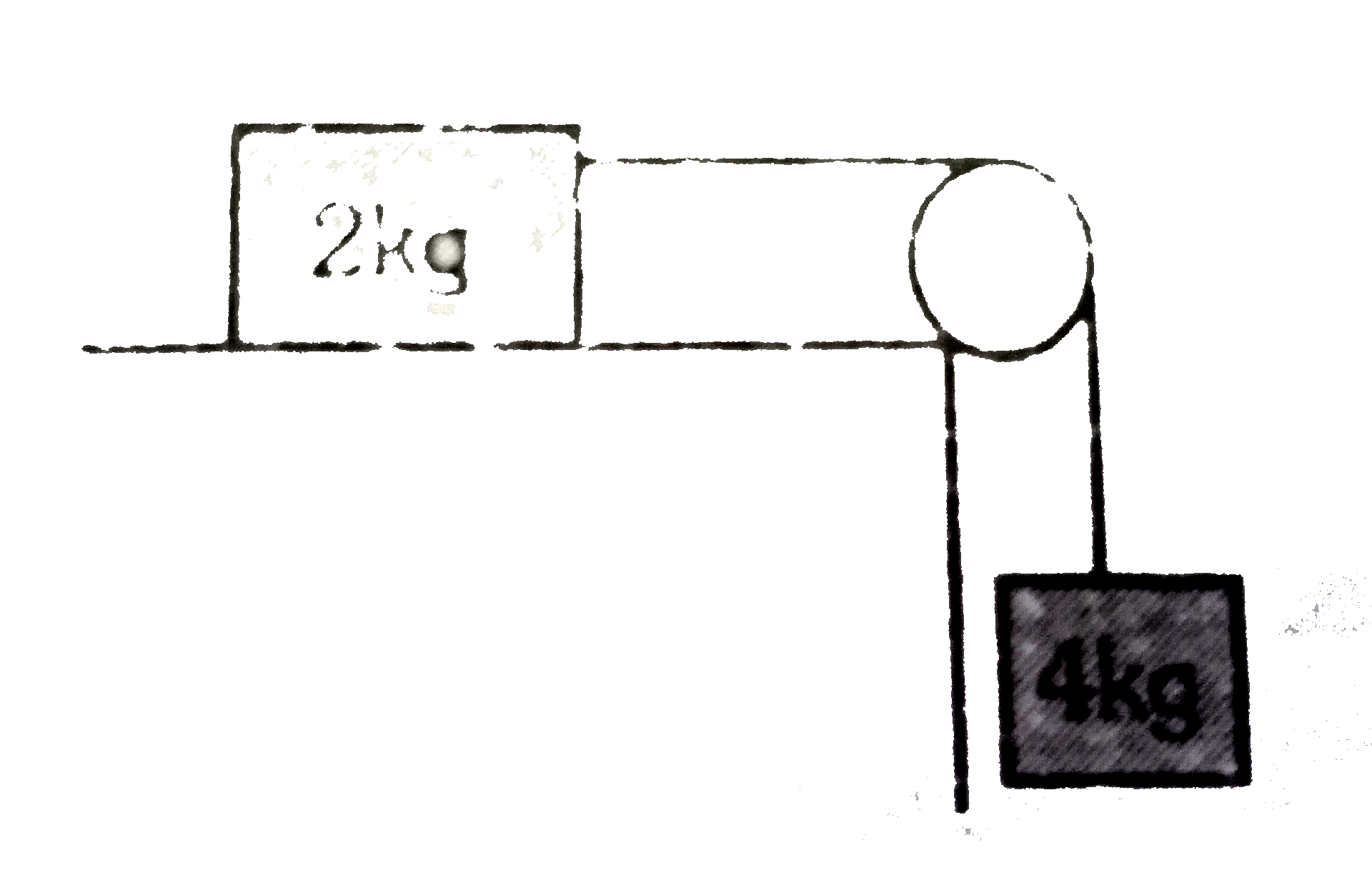
View SolutionA block of mass 10kg is pushed up on a smooth incline plane of inclination 30∘, so that it has acceleration 2m/s2. The applied force is
View SolutionA block of mass 1kg is at rest relative to a smooth wedge moving leftwards with constant acceleration a=5m/s−2 .Let N be the normal reation between the block and the wedge . Then (g=10m/s−2)

View Solution
