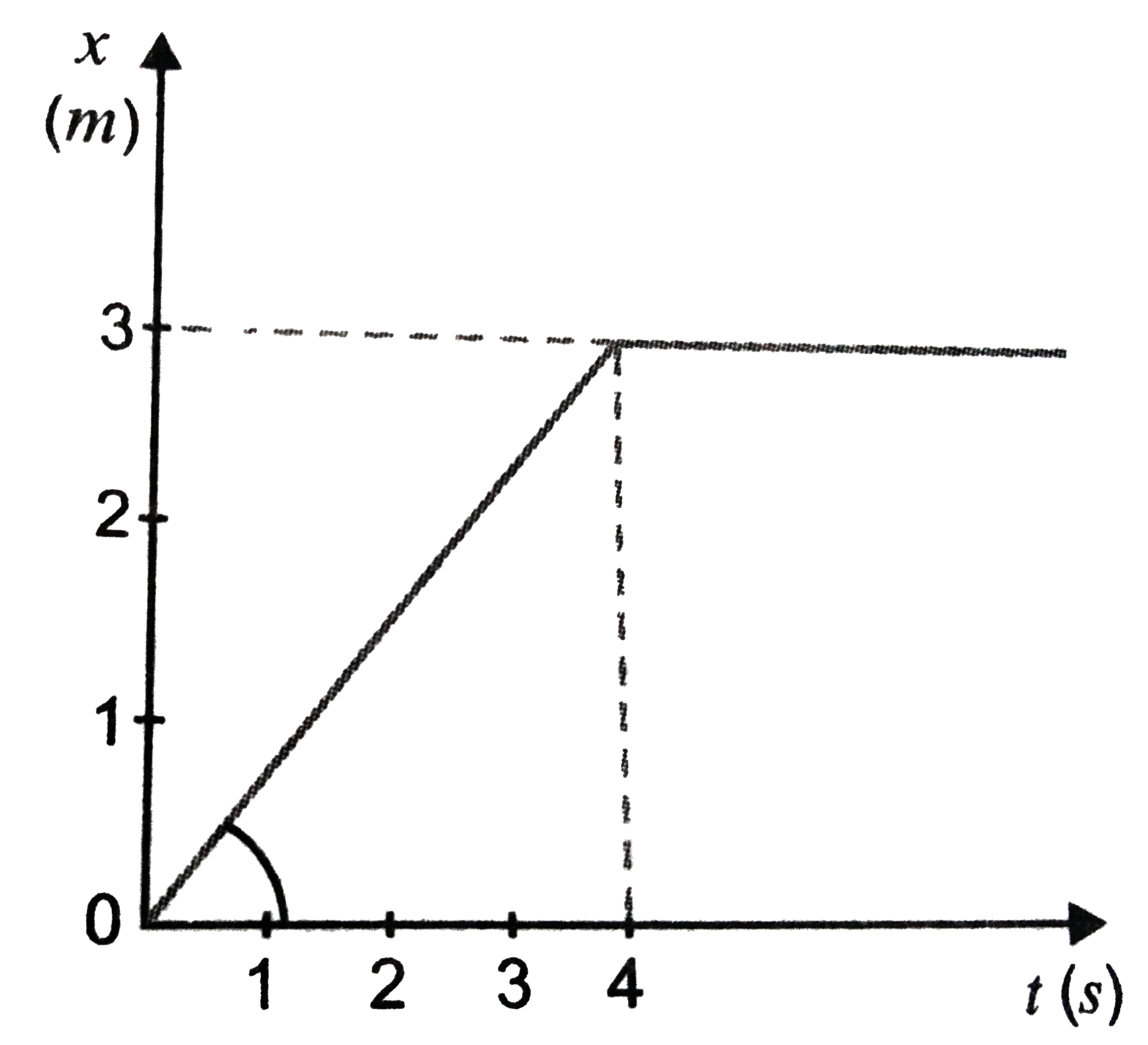
Fig. shows the position-time graph of a particle of mass 4 kg. What is the (i) force acting on the particle for t<0,t<4s,0<t<4s? (ii) impulse at t = 0 and t = 4 s? Assume that the motion is one dimensional.
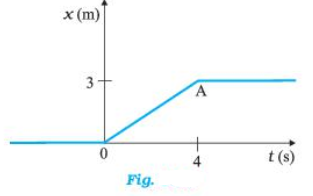
(a) When t lt 0 . As this part is horizontal , thus it can be concluded that distance covered by the particle is zero and hence force on the particle is zero .
When 0 lt t lt 4s . As OA has a constant slope, hence in this interval , particle moves with constant velocity ( 3/4 = 0.75 ms−1 . Hence force on the particle is zero.
When t gt 4s. As this portion shows that particle always remains at a distance of 3m from the origin i.e. the particle is at rest. Hence force on the particle is zero.
(b) Impulse at t = 0 . Here u = 0 , v = 0.75 ms−1 , M = 4 kg
∴ Impulse = total change in momentum = Mv - Mu
= M(v-u) = 4(0.75 - 0) = 3 kg ms−1 .
Impulse at t = 4s. Here u = 0.75 ms−1 , v = 0
∴ Impulse=M(v−u)=4(0−0.75)=−3kgms^(-1).
Topper's Solved these Questions
Similar Questions
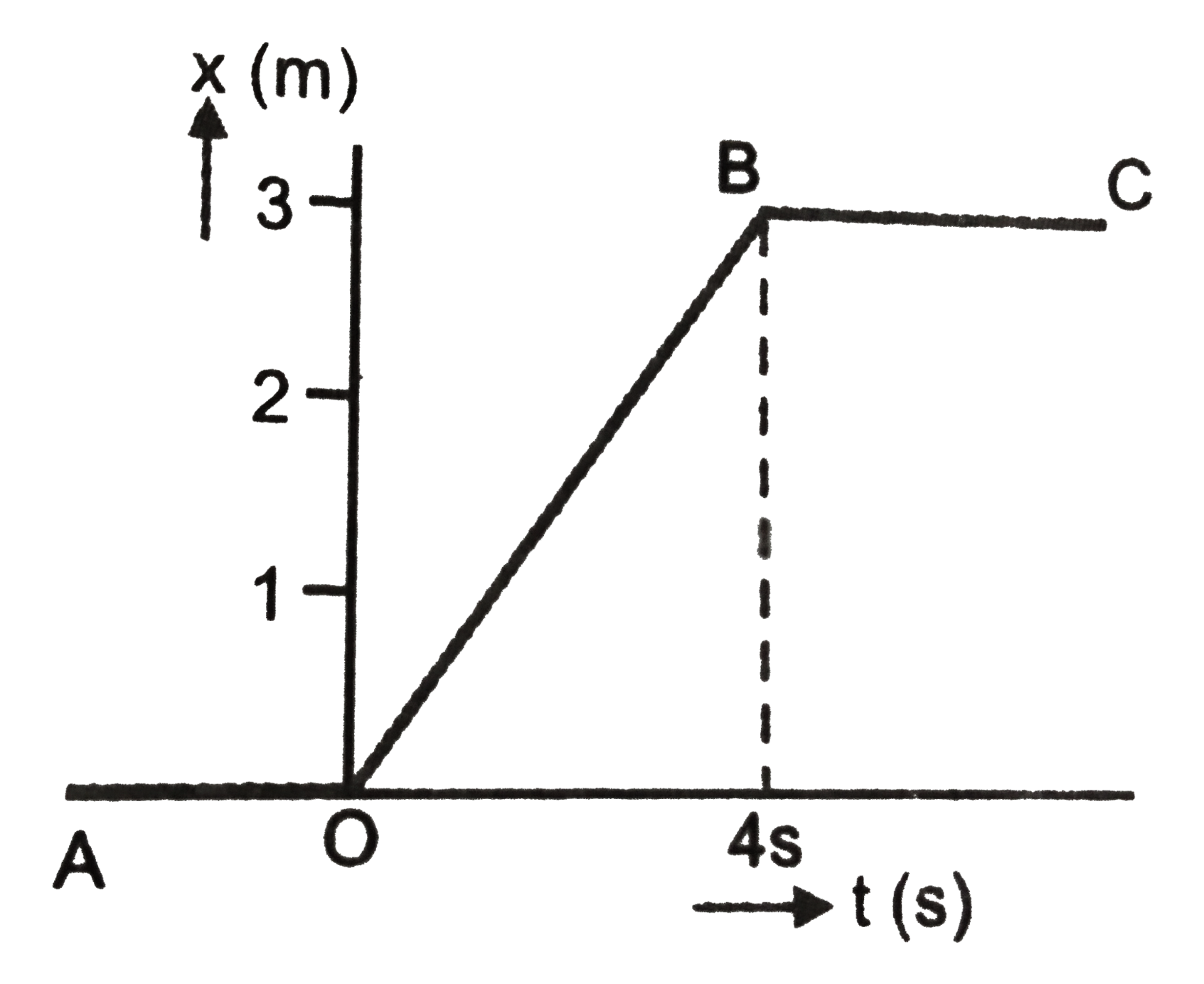
Shown the position time graph of a particle of mass 4 kg What is the force on the particle for t<0,0<t<4s motion only
 .
.
View SolutionFig. shows the position-time graph of a particle of mass 4 kg. What is the (i) force acting on the particle for t<0,t<4s,0<t<4s? (ii) impulse at t = 0 and t = 4 s? Assume that the motion is one dimensional.
View Solution
Knowledge Check
Figure shows the position time graph of a particle of mass 5kg. The force acting on the particle for 0<t<4s and 8s<t<12s respectively are,
 A5N,5NB5N.7.5NC5N,10ND0N,0N
A5N,5NB5N.7.5NC5N,10ND0N,0NPosition time graph of a particle of mass 2 kg is shown in figrure. Total work done on the particle from t=0 to t=4s is
 A8 JB4 JC0 JDCan't be determined
A8 JB4 JC0 JDCan't be determinedFigure shows the position-time graph of a particle of mass 4kg. Let the force on the particle for t<0 , 0<tlt,4s , t>4s be F1,F2 and F3 respectively. Then
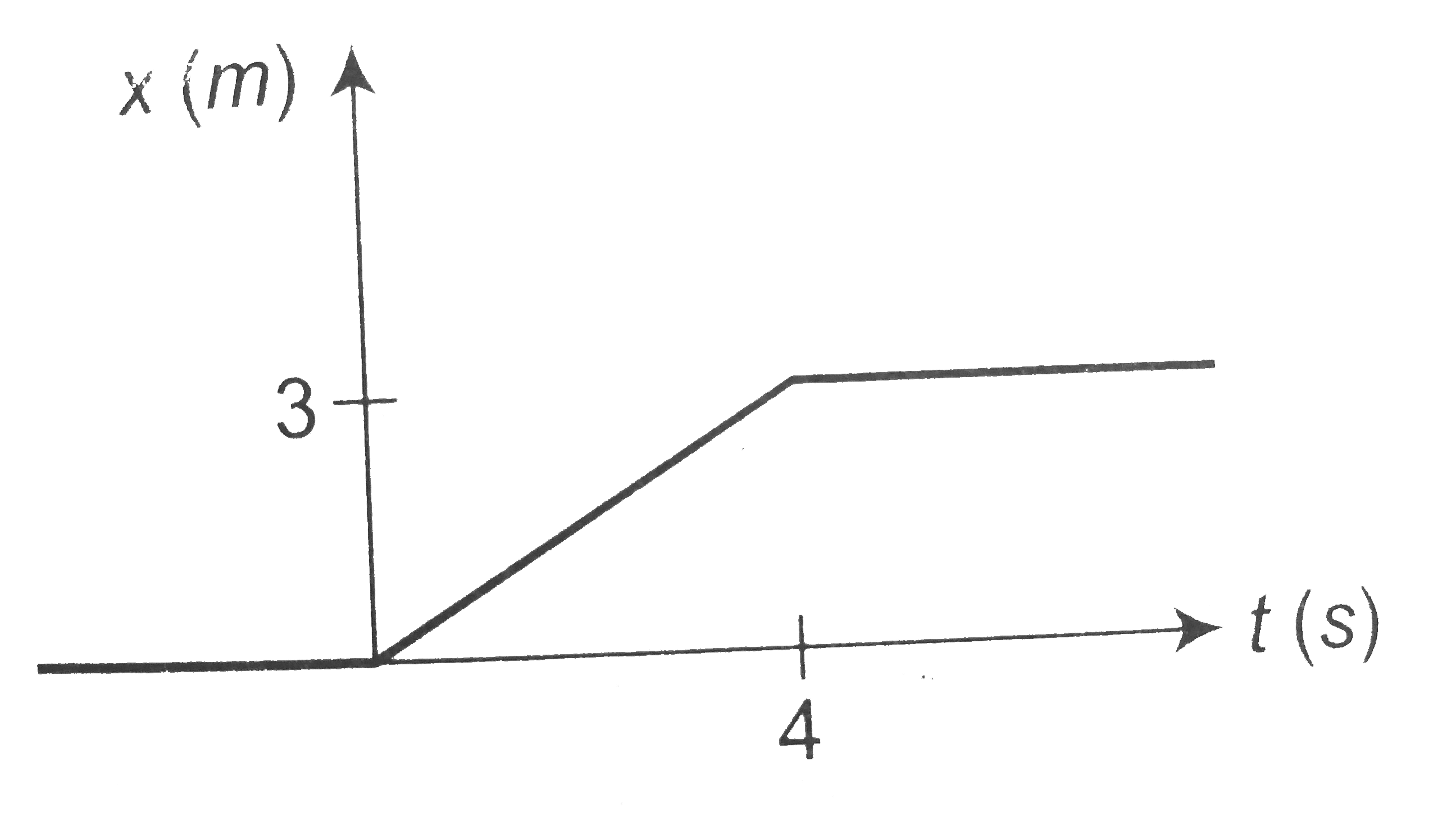 AF1=F2=F3=0BF1>F2=F3CF1>F2>F3DF1<F2<F3
AF1=F2=F3=0BF1>F2=F3CF1>F2>F3DF1<F2<F3
The position-time graph of a particle of mass 0.1 kg is shown. The impulse at t = 2s is :

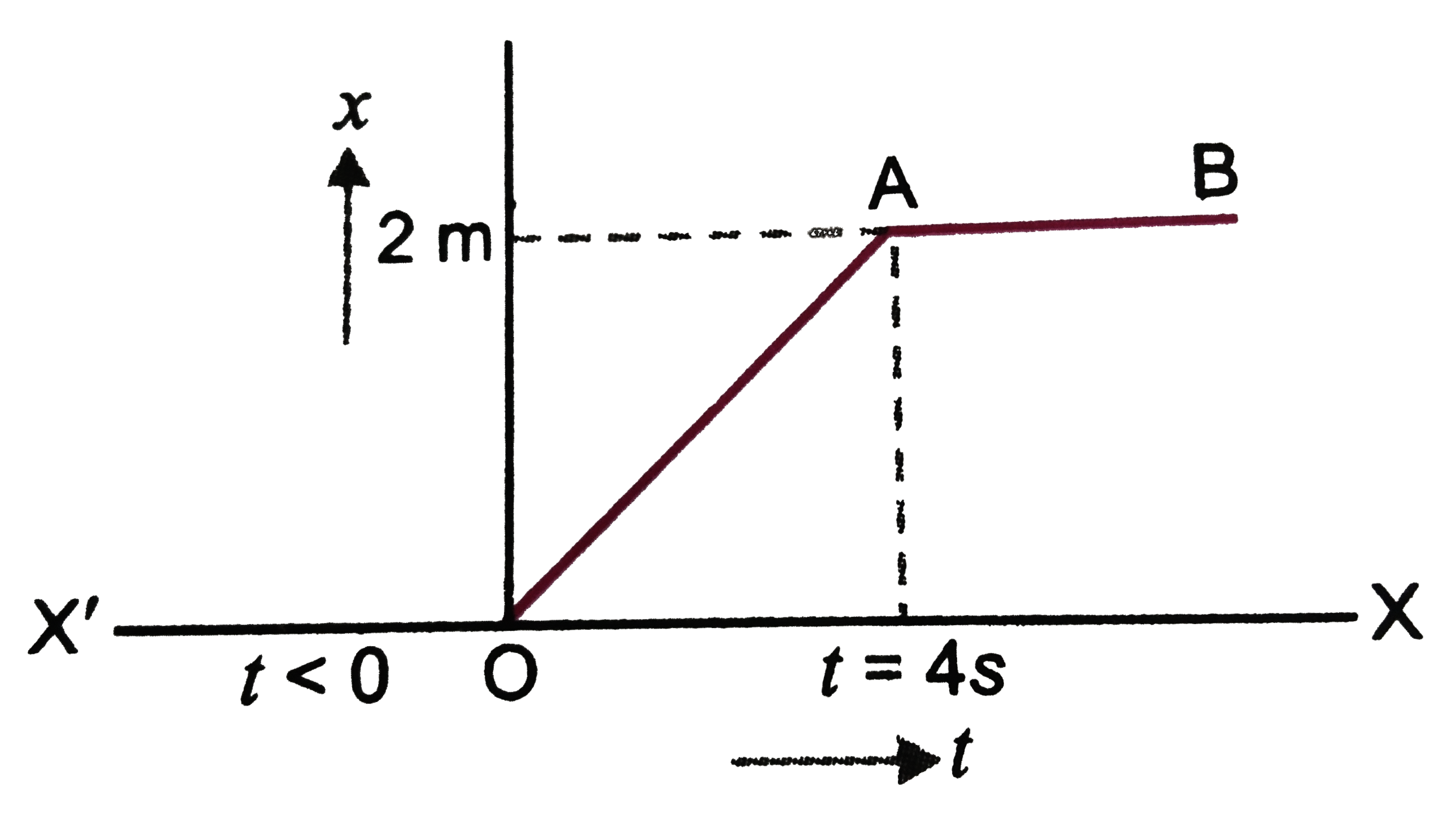
View SolutionShows position time graph of a particle of mass 100g Find the impulse at t=0 and at t=4s
 .
.
View SolutionThe position time graph of a body of mass 2kg is as given in What is the impulse on the body at t=0 s and t=4s ?
 .
.
View SolutionThe position-time graph of a particle of mass 0.1 kg is shown. The impulse at t = 2s is :

View SolutionIn the figure given, the position-time graph of a particle of mass 0.1 kg is shown the impulse at t = 2s is
View Solution
