Fig. shows two blocks of masses m1=3kg and m2=5kg both moving towards right on a frictionless surface with speed 10m/s and 4m/s respectively. To the back compression of the spring when the blocks collide?
m1=3kg,m2=5kg
u1=10m/s,u2=4m/s
k=1000N/m
Let v be the speed of the combination.
Using law of conservation of linear momentum,
m1u1+m2u2=(m1+m2)v
v=m1u1+m2u2m1+m2
=3×10+5×43+5=6.25m/s2
12m1u21+12m2u22=12(m1+m2)v2+12kx2
12×(3×102)+12×5×42=12×8×6.252+12×1000x2
500x2=380−312.5=67.5
x=√67.5500=0.367m=0.367m.

Topper's Solved these Questions
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - ADDITIONAL SOLVED PROBLEMS
138 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS
20 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems
30 Videos
Similar Questions
Two blocks of masses m1=2kg and m2=5 kg are moving in the same direction along a frictionless surface with speeds 10m/s and 3m/s, respectively, m2 being ahead of m1. An ideal spring with k=1120N/m is attached to the back side of m2. Find the maximum compression of the spring when the blocks collide. What are the final velocities of the blocks when they separate?
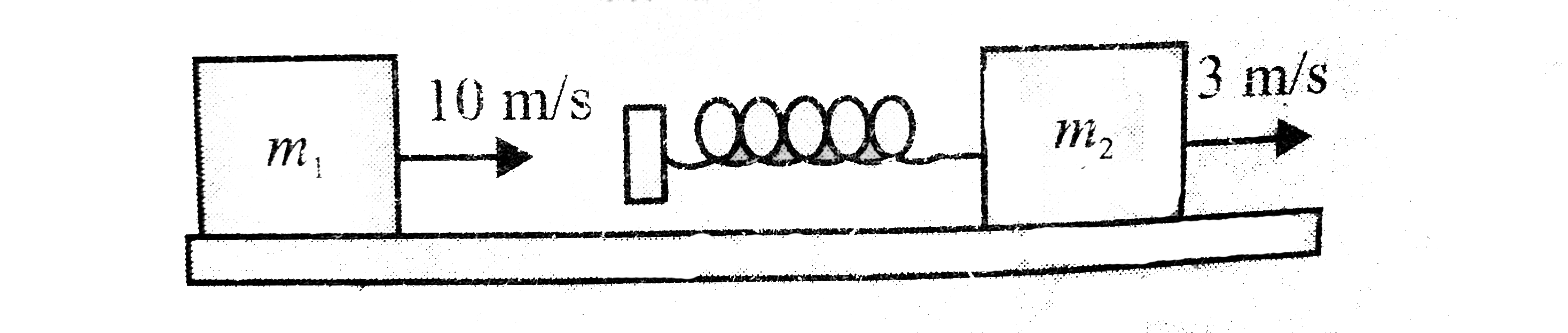
View SolutionTwo blocks of masses m1=2kg and m2=5 kg are moving in the same direction along a frictionless surface with speeds 10m/s and 3m/s, respectively, m2 being ahead of m1. An ideal spring with k=1120N/m is attached to the back side of m2. Find the maximum compression of the spring when the blocks collide. What are the final velocities of the blocks when they separate?
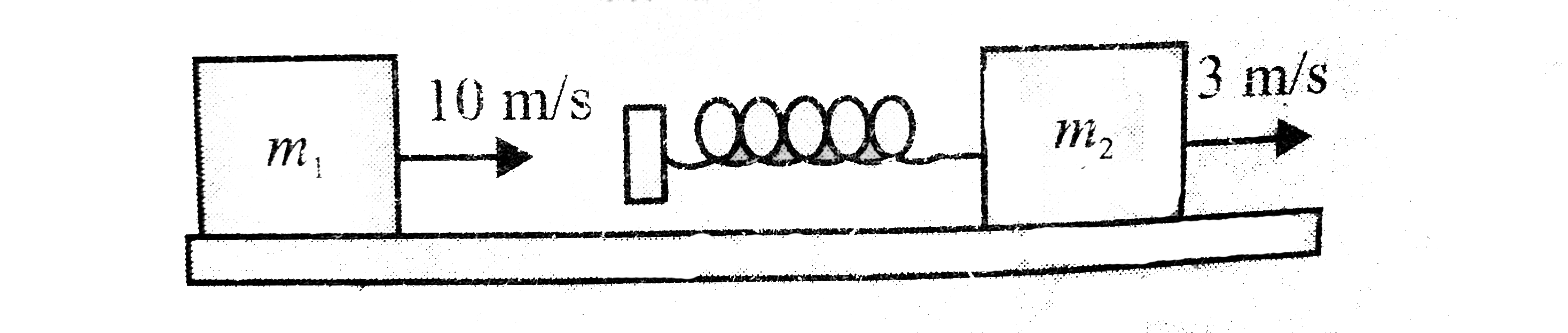
View Solution
Knowledge Check
Two blocks of masses m1=2kg and m2=4kg are moving in the same direction with speeds v1=6m/s and v2=3m/s, respectively on a frictionless surface as shown in the figure. An ideal spring with spring constant k=30000N/m is attached to the back side of m2. Then the maximum compression of the spring after collision will be
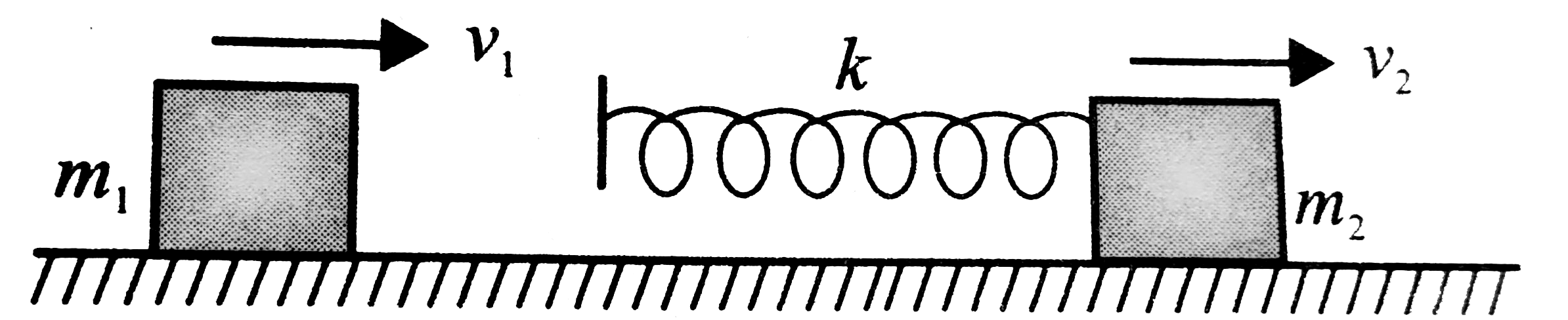 A0.06mB0.04mC0.02mDnone of these
A0.06mB0.04mC0.02mDnone of theseTwo blocks of masses 1kg and 3kg are moving with velocities 2m/s and 1m/s , respectively , as shown. If the spring constant is 75N/m , the maximum compression of the spring is
 A5cmB2cmC3cmD4cm
A5cmB2cmC3cmD4cmA block of mass 4kg slides on a horizontal frictionless surface with a speed of 2m/s. It is brought to rest in compressing a spring in its path. If the force constant of the spring is 400N/m, by how much the spring will be compressed
A2×10−2mB0.2mC20mD200m
Two blocks of masses m1=2kg and m2=4kg are moving in the same direction with speeds v1=6m/s and v2=3m/s, respectively on a frictionless surface as shown in the figure. An ideal spring with spring constant k=30000N/m is attached to the back side of m2. Then the maximum compression of the spring after collision will be
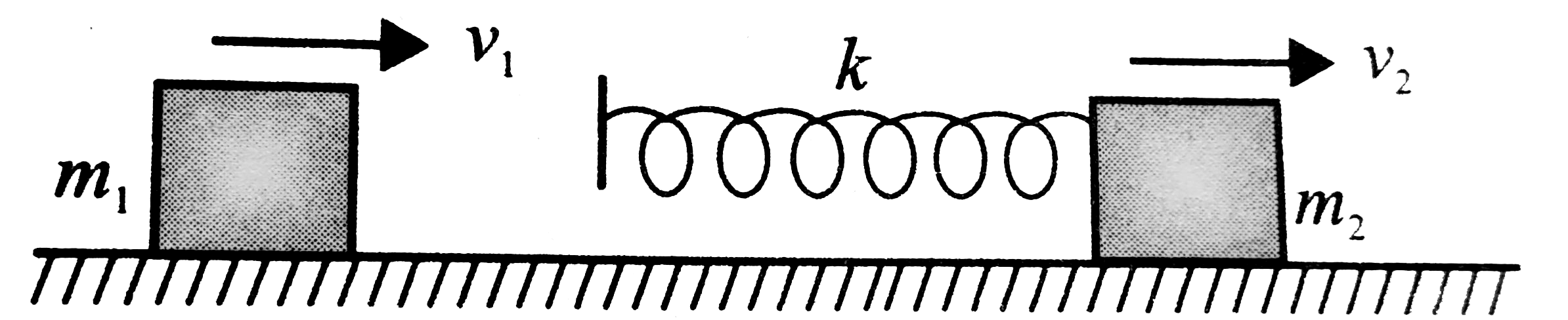
View SolutionTwo particles A and B of masses 2kg and 3kg moving on a smooth horizontal surface with speed 1m/s and 2m/s collides perfectly inelastically, then

View SolutionTwo particles A and B of masses 2kg and 3kg moving on a smooth horizontal surface with speed 1m/s and 2m/s collides perfectly inelastically, then

View SolutionThe blocks ov mass m1=1kg and m2=2kg are connected by an ideal spring, rest on a rough horizontal surface. The spring is unstressed. The spring constant of spring is K=2N/m. The coefficient of friction between blocks and horizontal surface is μ=12. Now the left block is imparted a velocity u towards right as shown. The largest value of u( in m/s) such that the block of mass m2 never moves is ( Take g=10m/s2)
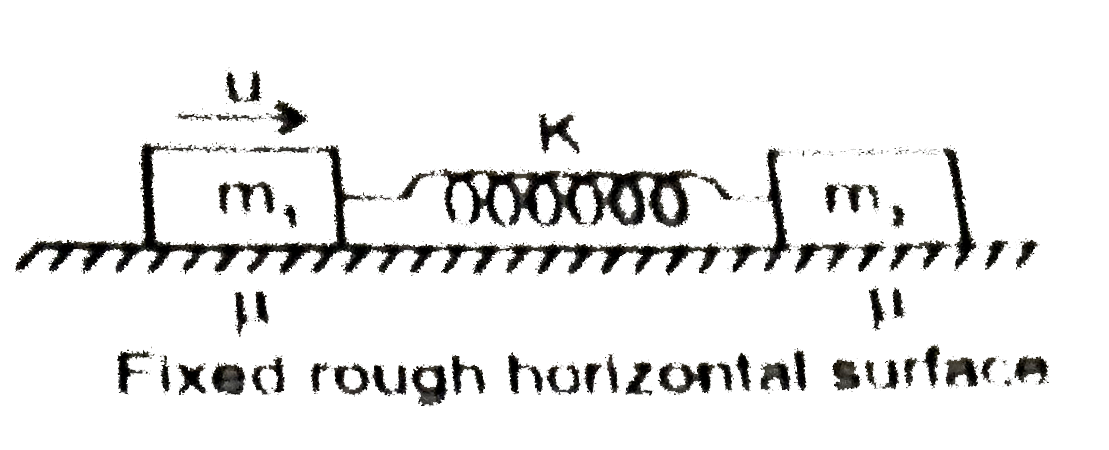
View SolutionThe blocks ov mass m1kg and m2=2kg are connected by an ideal spring, rest on a rough horizontal surface. The spring is unstressed. The spring constant of spring is K=2N/m. The coefficient of friction between blocks and horizontal surface is μ=12. Now the left block is imparted a velocity u towards right as shown. The largest value of u( in m/s) such that the block of mass m2 never moves is ( Take g=10m/s2)
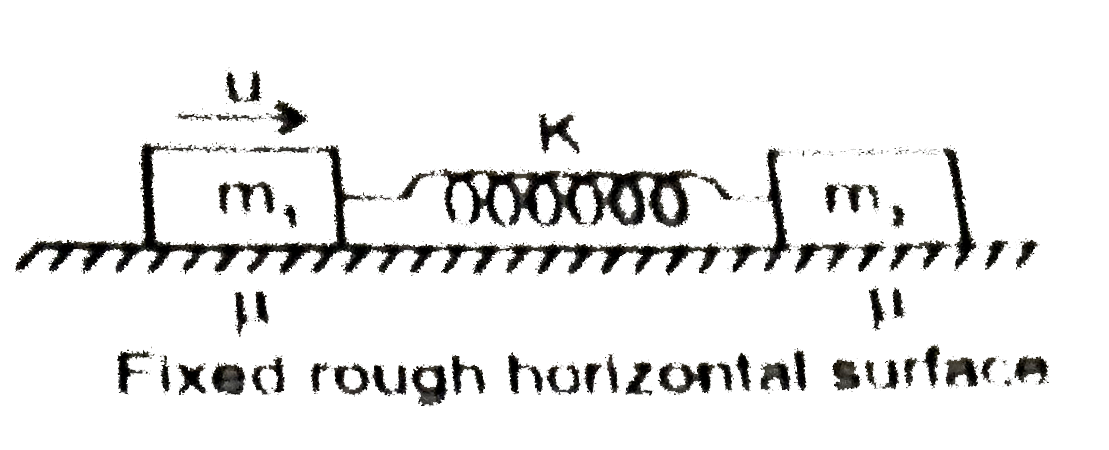
View Solution
